§ 10. Множественная корреляция и регрессия

Все рассмотренные до сих пор различные задачи анализа взаимосвязи имели ту общую черту, что в них рассматривалась зависимость результативного признака от одного признака-фактора. В этом параграфе мы рассмотрим более сложный случай: нам предстоит исследовать зависимость некоторого результативного признака (обозначим его x₀) от нескольких факторов .

Сложность такой задачи определяется тем, что различные факторы воздействуют на результативный признак не изолированно, и зависимость от набора факторов не есть простая сумма зависимостей от каждого из факторов в отдельности. Взаимосвязь результативного признака с набором факторов приходится исследовать на фоне взаимосвязи между факторами. Таким образом, анализ множественных зависимостей приходится производить, рассматривая сложные сети взаимосвязей. Схематически структуру таких сетей изображают в виде схемы связей (рис. 10.1).

Рис. 10.1

Различные признаки изображаются в виде кружков на плоскости, а связи между ними обозначаются стрелками. Над стрелками могут быть указаны определенные количественные характеристики зависимостей (например, коэффициенты корреляции). На рисунке представлена схема связей результативного признака x₀ с четырьмя факторами. При этом все факторы связаны друг с другом, так что общее число рассматриваемых связей равно 10.

Задача эмпирически-регрессионного описания множественной зависимости в принципе решается так же, как и для случая одного фактора. Но теперь множество наблюдений необходимо разбить на группы, однородные по всем факторам. Так, например, если исследуется зависимость заработной платы рабочих от профессии, квалификации, возраста, стажа и образования, то в одну группу войдут, скажем, токари 2-го разряда в возрасте 20–25 лет, со стажем работы 3–5 лет, с общим средним образованием. Токари того же разряда, с тем же возрастом и стажем работы, но со средним специальным образованием образуют уже другую группу и т.д.

Число таких групп весьма велико даже при сравнительно небольшом числе факторов. Введением нового фактора, принимающего k значений, разбивает каждую из уже имеющихся групп на k частей. Если рассматривается m факторов, принимающих соответственно значений каждый, то общее число групп окажется равно .

Если в рассматриваемом примере мы разобьем рабочих на 5 профессиональных групп, 6 квалификационных разрядов, 5 возрастных групп, 4 группы по стажу и 3 группы по образованию, то общее число групп окажется равным

1800.

Как отмечалось выше, для получения статистически устойчивых значений групповых средних необходимо, чтобы все группы были представлены достаточным числом наблюдений. Каков же должен быть объем совокупности, чтобы 1800 групп были хорошо заполнены!

Таким образом, трудности, связанные с обеспечением достаточного числа наблюдений в каждой группе, которые мы отметили при анализе парной связи, при переходе к множественной связи многократно усугубляются, и метод становится практически неприемлемым при числе факторов, большем двух-трех.

Аналитические приемы исследования взаимосвязи при исследовании множественных зависимостей приобретают поэтому особую ценность. Как отмечалось выше, статистическая устойчивость результатов анализа существенно зависит от числа параметров регрессии, оцениваемых по данному наблюдению. Многие важные свойства зависимостей могут быть исследованы с помощью функций, содержащих небольшое число параметров, так что во многих практически интересных случаях аналитические методы могут обеспечить надежный, статистически устойчивый результат.

Прежде чем перейти к описанию формальных вычислительных процедур анализа, следует отметить особо важную роль качественного анализа при исследовании множественных зависимостей. Хотя последнее слово в решении вопросов «есть ли зависимость?» и «какова эта зависимость?» — принадлежит статистическому анализу, но отбор факторов, «подозреваемых во влиянии» на результативный признак, и содержательная интерпретация результата исследования требуют от исследователя глубокого знания закономерностей анализируемого объекта.

Наиболее распространенные аналитические приемы исследования множественных зависимостей, так же, как и парных взаимосвязей, базируются на методе наименьших квадратов. Математически эти методы сводятся к тому, что из семейства функций переменных, содержащих m неизвестных параметров требуется выбрать такую, для которой остаточная дисперсия принимает наименьшее значение:

Заметим, что в § 5 при выводе системы нормальных уравнений в общем виде не использовался тот факт, что рассматривались функции одной переменной; существенным было лишь число параметров функции. Поэтому мы можем здесь воспроизвести без доказательства систему уравнений в виде сумм (5.2):

и в виде средних (5.3):

Любая из этих систем пригодна для определения параметров множественной регрессии.

Перейдем к рассмотрению линейной множественной регрессии. Линейная зависимость от m переменных описывается следующим выражением:

Число параметров уравнения равно m+1. Для составления нормальных уравнений найдем частные производные функции  по всем параметрам:

Система нормальных уравнений принимает вид:

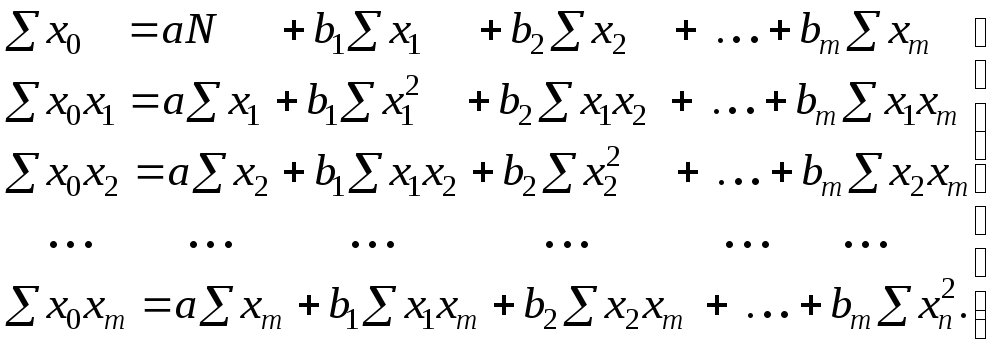(10.1)

Эту же систему можно записать в форме средних:

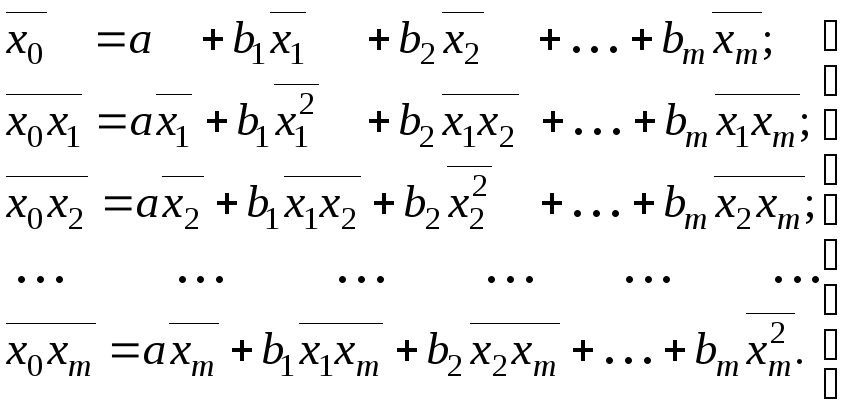(10.2)

Каждая из систем (10.1) и (10.2) состоит из m1 уравнений и содержит m1 неизвестную величину: свободный член a и m коэффициентов b_i. Порядок системы может быть понижен на единицу. Для этого умножим начальное уравнение системы (10.2) почленно на :

i  1, 2, …, m.

Затем почленно вычтем получившиеся выражения из последующих уравнений системы, которые при этом примут следующий вид:

i  1, 2, …, m.

Таким образом, мы исключили из системы одну неизвестную — свободный член a — и уменьшили на единицу число уравнений. Заметим, что в левых частях уравнений и в скобках стоят ковариации соответствующих переменных, так что теперь систему нормальных уравнений можно представить в виде

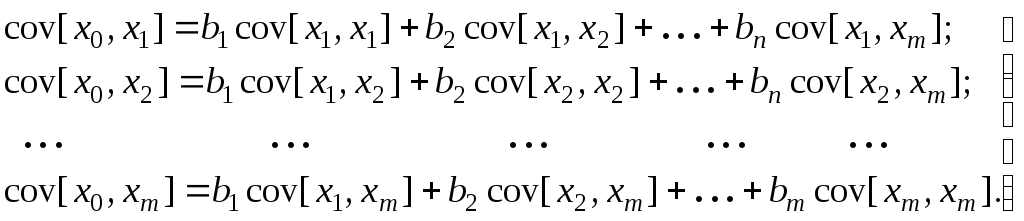
(10.3)

Диагональные элементы матрицы такой системы — это дисперсии факторных переменных: ²[x_i]  cov[x_i, x_i]. Из системы (10.3) видно, что коэффициенты b_i множественной линейной регрессии полностью определяются ковариациями всех пар признаков. После нахождения коэффициентов b_i свободный член может быть найден из начального уравнения системы (10.2):

Системы уравнений (10.1) — (10.3), как мы видим, могут быть использованы для определения неизвестных параметров регрессии в естественных масштабах. Однако более глубокие результаты могут быть получены при анализе уравнения регрессии в стандартных масштабах.

Уравнение регрессии для нормированных отклонений имеет следующий вид:

.

Для определения параметров  и  воспользуемся системой (10.2). Первое из этих уравнений с учетом свойств нормированных отклонений показывает, что . Таким образом, уравнение регрессии в стандартных масштабах не содержит свободного члена:

. (10.4)

Приведем остальные уравнения, учитывая, что 0:

Используем уже известные свойства нормированных отклонений:

Здесь мы для краткости используем обозначения r_ij для коэффициента корреляции между признаками вместо более громоздкого обозначения r[x_i, x_j].

Система уравнений для коэффициентов  принимает вид:

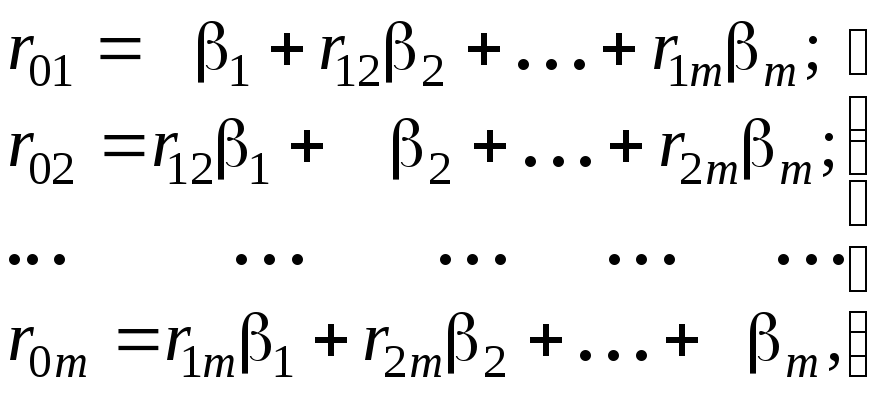(10.5)

или, в свернутом виде:

r_0i = r_1i₁ + r_2i₂ + … + r_im_m , i = 1, 2, … , m. (10.6)

Здесь использовано очевидные равенства r_ii = 1 для всех i.

Составление системы (10.5) удобно выполнять в следующем порядке. Определяются все парные коэффициенты корреляции и сводятся затем в так называемую корреляционную матрицу:

	0	1	2		m
0	1
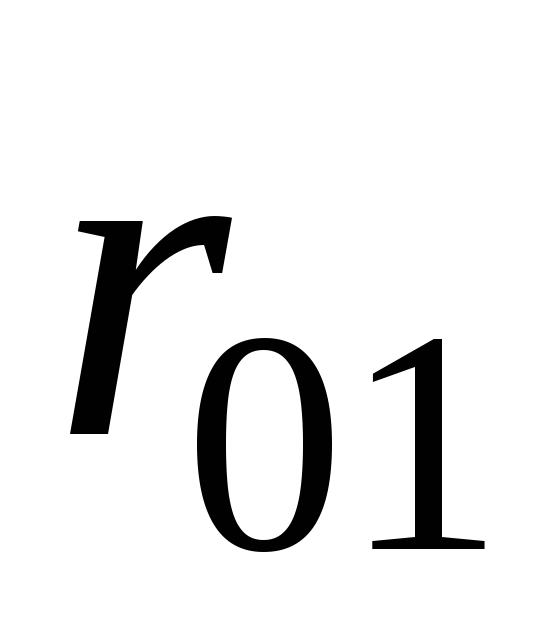
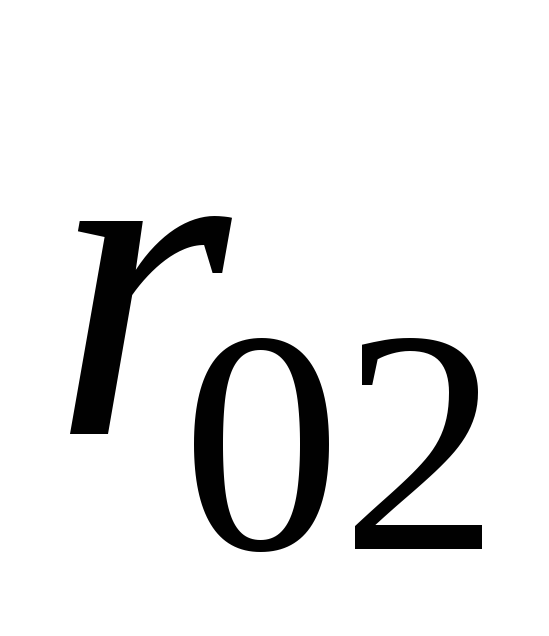
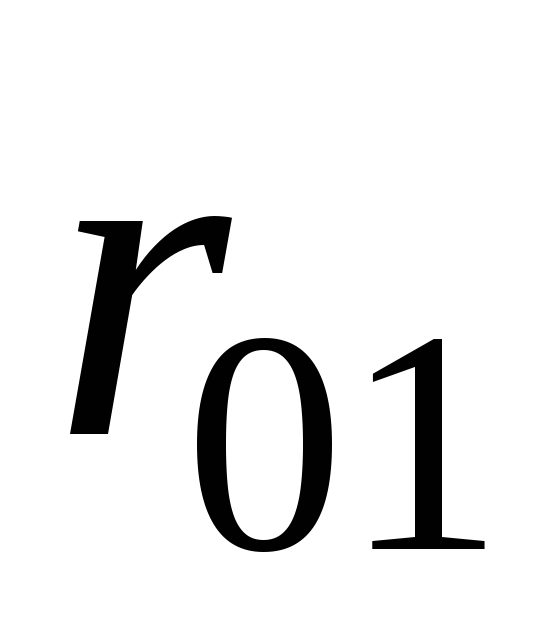
1		1
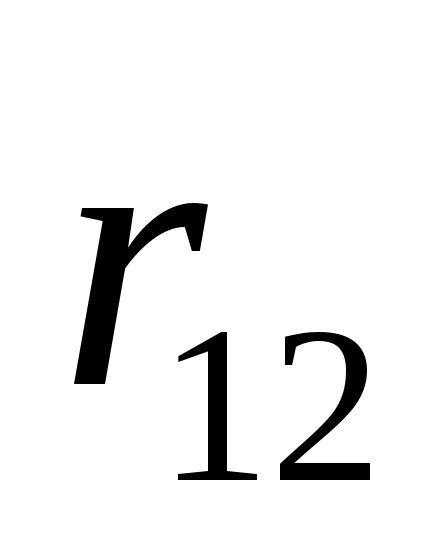
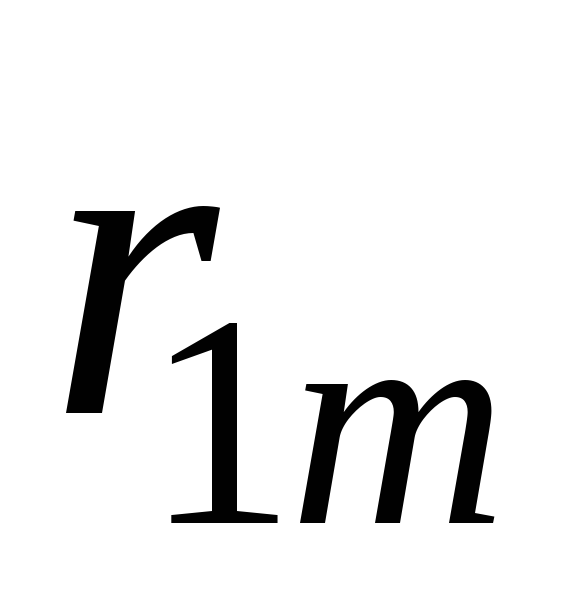
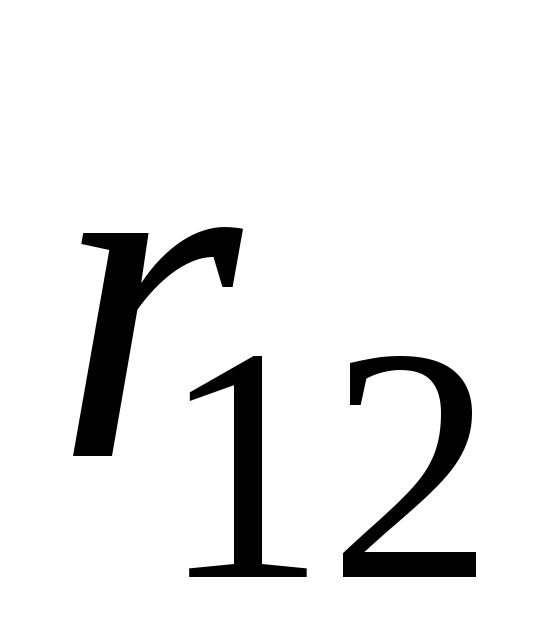
2			1
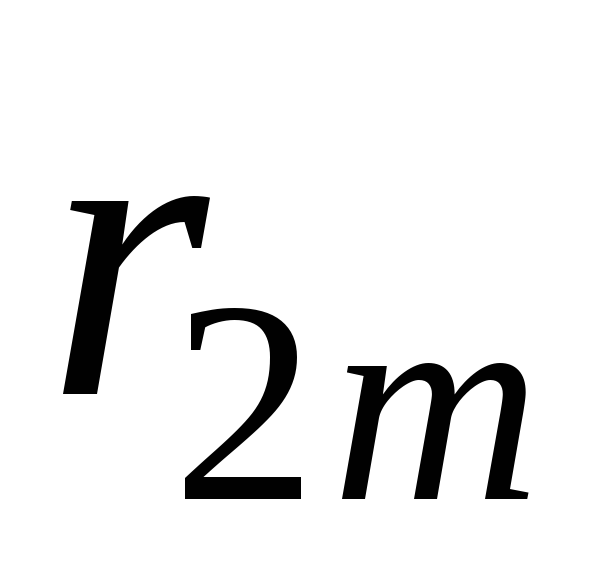
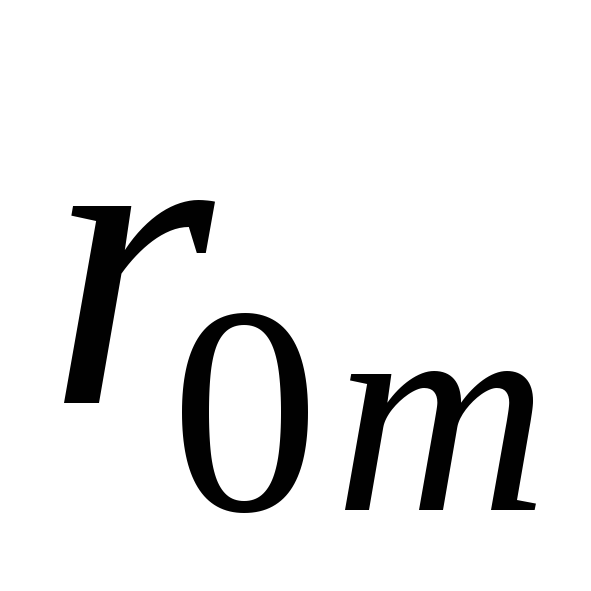
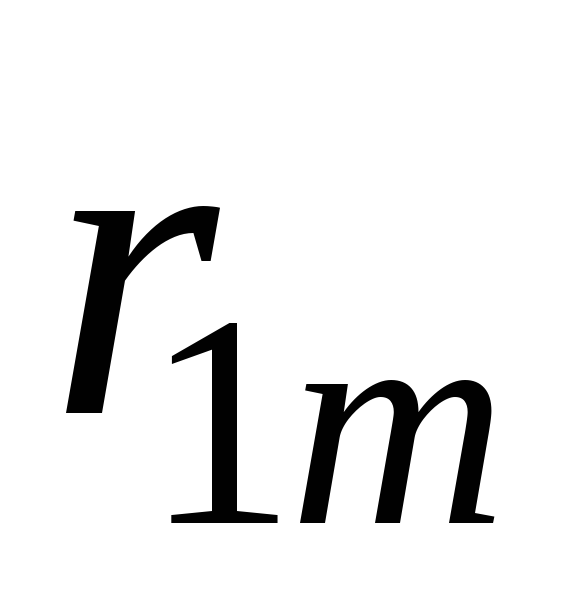
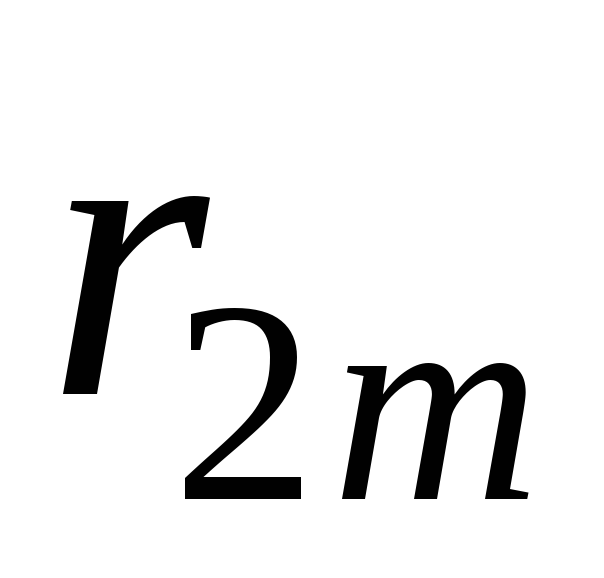
m					1

Корреляционная матрица включает значения коэффициентов корреляции каждого признака с каждым из остальных. Так как , то общее число различных коэффициентов корреляции равно , где m — число признаков-факторов.

Если в корреляционной матрице отбросить строку «0», то оставшиеся элементы повторяют значения коэффициентов в системе уравнений (10.5): столбец «0» образует столбец левых частей, столбец «1» — коэффициенты при _, столбец «2» — коэффициенты при _ и т.д.

Решением этой системы уравнений является набор коэффициентов уравнений в стандартных масштабах. Эти коэффициенты обычно называют -коэффициентами.

От уравнения в стандартных масштабах

нетрудно перейти к уравнению в естественных масштабах. Используем выражения для нормированных отклонений:

Отсюда

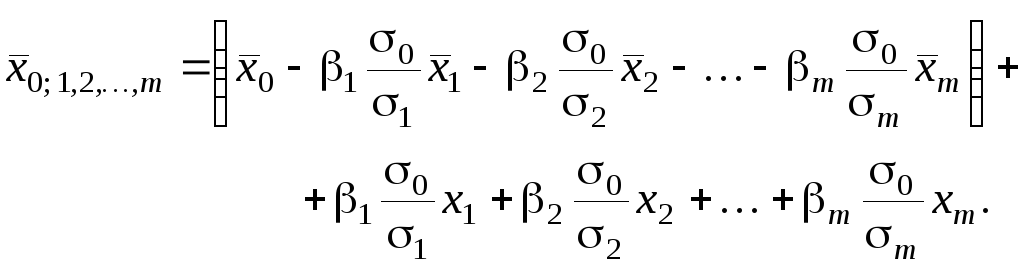
Это равенство по виду совпадает с уравнением регрессии в естественных масштабах:

параметры которого определяются равенствами:

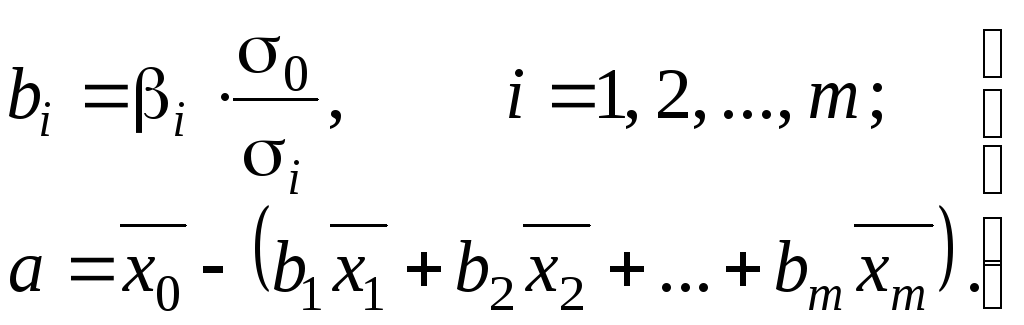(10.7)

Перейдем теперь к оценке тесноты связи и определим корреляционное отношение, которое применительно к множественной линейной регрессии носит название коэффициента множественной корреляции. Обычно он обозначается буквой R; в индексе, если нужно уточнение, приводятся обозначения результирующей переменной и факторов, аналогичные обозначению регрессии. Так, коэффициент множественной корреляции для зависимости переменной x₀ от факторов x₁, x₂, x₃ обозначается R_{0; 1, 2, 3} или R_{0 | 1, 2, 3} .

Определим корреляционное отношение для регрессии в стандартных масштабах; так как обе функции различаются лишь масштабами, значения корреляционного отношения для них совпадают.

Найдем остаточную дисперсию :

.

Первое слагаемое в полученном выражении в силу известного свойства нормированных отклонений равно 1; так как , то

Третье слагаемое требует более сложных преобразований. Так как величина суммы не зависит от обозначения номеров слагаемых, то

.

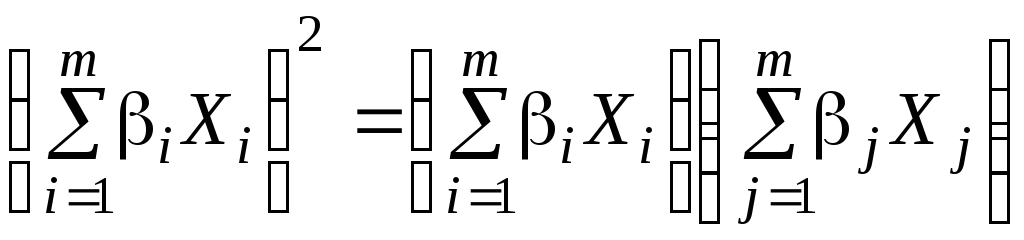Внесем вторую сумму «в скобки», умножив на нее каждое из слагаемых , а затем внесем X_i во внутреннюю сумму:

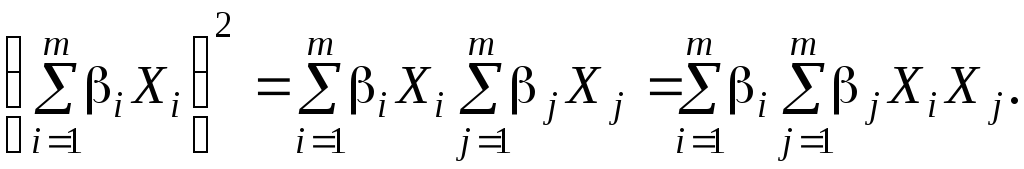
Выполним усреднение с учетом равенства (10.6):

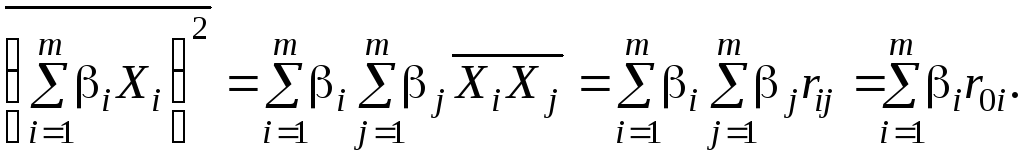
Таким образом, мы получили следующее выражение для остаточной дисперсии переменной :

Так как полная дисперсия X₀ равна единице, то для квадрата коэффициента множественной корреляции справедливо выражение

или, окончательно,

(10.8)

Расчет параметров множественной регрессии рассмотрим на следующем условном примере. Допустим, что на множестве небольших предприятий исследуется зависимость расходов на управление от различных факторов. Одним из факторов, очевидно, является численность персонала: чем больше работников занятых на предприятии, тем больше и расходы, связанные с управлением персоналом. С другой стороны, сложность управления предприятием тем выше, чем больше номенклатура продукции, т.е. число наименований ее видов. Следовательно, расходы на управление должны зависеть и от этого фактора. Ограничим анализ исследованием зависимости от двух названных факторов. Допустим, что данные статистического наблюдения уже подверглись определенной статистической обработке и получены средние значения всех признаков, средние квадратические отклонения и все парные коэффициенты корреляции (число их равно трем: расходы на управление — численность персонала; расходы на управление — номенклатура продукции; численность персонала — номенклатура продукции).

Эти промежуточные результаты приведены в таблице 11.1.

Таблица 11.1. Данные для расчета двухфакторной линейной регрессии

Признак		Среднее значение	Среднее квадратическое отклонение	Коэффициенты корреляции с признаками
Обозна-чение	Наименование			x0	x1	x2
x0	Расходы на управление, тыс. руб/мес.	200	50	1.0	0.8	0.7
x1	Численность персонала, чел.	100	20	0.8	1.0	0.5
x2	Номенклатура, наименований	20	10	0.7	0.5	1.0

По корреляционной матрице составляем систему уравнений для -коэффициентов:

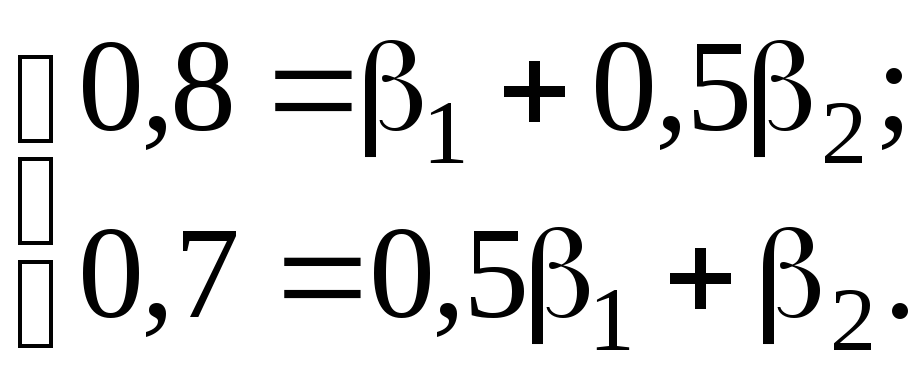
Решив эту систему, найдем:

Отсюда определим коэффициенты уравнения в естественных масштабах:

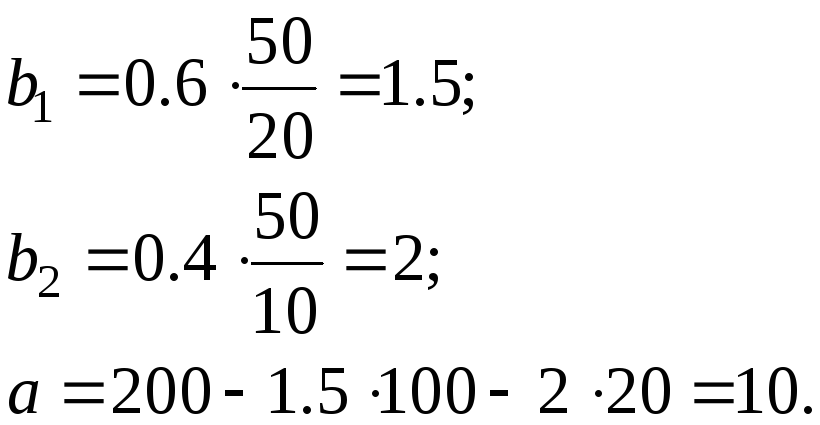
Таким образом, линейные уравнения регрессии имеют вид:

в стандартных масштабах:

в естественных масштабах:

С помощью равенства (11.8) определим коэффициент множественной корреляции:

Точность линейного уравнения регрессии в естественных масштабах можно оценить, вычислив остаточное среднее квадратическое отклонение:

При анализе взаимосвязи результирующего признака с несколькими факторами в распоряжении исследователя оказывается большое число различных численных характеристик связи: парные коэффициенты корреляции, коэффициенты парных уравнений регрессии,-коэффициенты, коэффициенты уравнения множественной регрессии, множественный коэффициент корреляции. Остановимся подробнее на смысле каждого из этих показателей.

При анализе зависимости от всех факторов получают уравнение множественной регрессии вида:

Коэффициенты регрессии в этом уравнении показывают интенсивность влияния i-го фактора на результирующий признак при неизменности значений всех остальных факторов, учитываемых в данной модели. Коэффициент регрессии b_i имеет определенное значение только для данного набора факторов. Если тот же i-й фактор использовать в составе другого набора, то интенсивность его влияния на ту же самую результирующую переменную окажется иной в связи с условием постоянства иных «прочих» факторов.

По каждому из факторов в отдельности может быть построено и парное уравнение регрессии вида

Здесь нет «прочих» факторов, и поэтому отсутствует ограничение на изменение каких-либо факторов; можно сказать, что коэффициент множественной регрессии отражает непосредственное влияние i-го фактора, а коэффициент b_(i) парного уравнения отражает полное влияние (как непосредственное, так и косвенное — через другие факторы, которые при этом изменяются в соответствии с их зависимостями как от , так и друг от друга).

Аналогичное соотношение существует между -коэффици­ентами и парными коэффициентами корреляции. -коэффици­енты отражают степень непосредственного влияния каждого фактора при условии постоянства всех остальных включенных в состав регрессии факторов; коэффициент парной корреляции отражает полное влияние некоторого фактора на результирующий признак. Это обстоятельство можно пояснить, вернувшись к системе уравнений (11.5), которую мы использовали для определения -коэффициентов. Полное влияние, например, первого фактора на результирующий признак описывается коэффициентом корреляции . На такую долю своего среднего квадратического отклонения изменится при изменении на . Эта величина складывается из непосредственного влияния () и влияния через остальные факторы: если не накладывать на их изменения никаких ограничений, то изменится на и соответственно изменит на величину , фактор изменится на и при этом изменит результативный признак на и т.д. Построим схему связей для рассмотренного выше примера (рис. 10.2). Здесь влияние факторов на указано -коэффициентами, а их взаимосвязь — коэффициентом корреляции. Из рисунка видно, что

что соответствует данным задачи.

Рис. 10.2

Рассмотрим еще один пример. Пусть дана корреляционная матрица:

	0	1	2
0	1.0	0.6	0.3
1	0.6	1.0	0.5
2	0.3	0.5	1.0

-коэффициенты определяются из системы уравнений

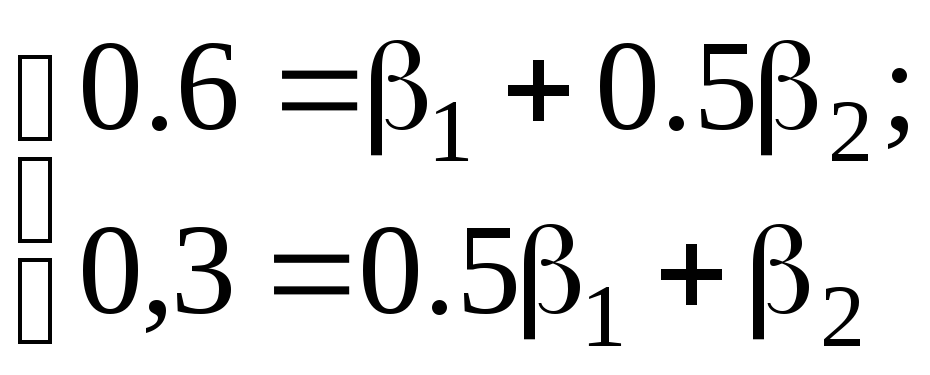
и равны

Таким образом, второй фактор непосредственно не влияет на результативный признак. Но коэффициент корреляции не равен нулю: фактор влияет на через фактор . Схема связей представлена на рис. 10.3.

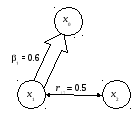
Рис. 10.3

Коэффициент множественной корреляции показывает тесноту связи результативного признака сразу со всеми факторами. Отметим, что коэффициент множественной корреляции не меньше (как правило, больше), чем абсолютная величина парного коэффициента корреляции результативного признака с любым фактором:

R  | r_0i |.

Это объясняется тем, что введение нового фактора может только уменьшить остаточную вариацию. Так как коэффициенты регрессии определяются по методу наименьших квадратов, не может случиться так, что введение нового фактора увеличит . В крайнем случае, новый фактор получит коэффициент 0, и остаточная вариация, а следовательно, и коэффициент множественной корреляции, останутся без изменений. Это означает, что влияние нового фактора уже полностью учтено прежними. В примере, представленном на рис. 10.2, оба фактора имеют ненулевые -коэффициенты, и

Определим коэффициент множественной корреляции для схемы связей, представленной на рис. 10.3:

Вообще равенство

означает, что только один фактор (x_k) непосредственно влияет на результат.

При анализе взаимосвязей целесообразно принимать во внимание лишь те факторы, которые непосредственно влияют на результативный признак. Это позволяет упростить анализ, не снижая его качества.