§ 2. Определение статистической взаимосвязи

Обычно мы говорим, что величина y зависит от x, или что x влияет на y в тех случаях, когда различным значениям x соответствуют различные значения y. Очевидно, такое определение непригодно для стохастической зависимости, так как в данном случае даже одним и тем же значениям x соответствуют различные значения величины y.

Так как признак y варьирует не только во всей совокупности, но также и в группах, однородных по признаку x, можно говорить о зависимости между x и y в статистическом смысле, только сопоставляя распределения по признаку y групп, соответствующих различным фиксированным значениям x. При этом признак y называется статистически независимым от признака x, если различные группы, каждая из которых однородна по признаку x, имеют одинаковое распределение по признаку y. В противном случае признаки называются статистически зависимыми.

Пусть, например, нам нужно ответить на два вопроса:

а) зависит ли величина заработной платы рабочего от его квалификации?

б) зависит ли размер обуви рабочего от его квалификации?

Исследуя каждую из этих зависимостей, мы должны разбить множество рабочих на группы, объединяющие рабочих одной квалификации, и сравнить распределения этих групп по величине заработной платы (в случае а) ) и по размеру обуви (в случае б) ). Возможные распределения представлены графически на рис. 2.1а и 2.1б соответственно. Так как гистограммы на рис. 2.1а характеризуют распределения групп как различные, а полигоны на рис. 2.1б — как одинаковые, на основании введенного определения можно сделать следующие выводы:

а) величина заработной платы зависит от квалификации;

б) размер обуви не зависит от квалификации рабочих.

Так как в случае статистической независимости все группы распределены одинаково, то каждая из них распределена так же, как и вся совокупность. Если признаки зависимы, то, по крайней мере, некоторые из групп распределены иначе, чем совокупность в целом.

а б

Рис. 2.1

Рис. 2.1

Приведенное определение зависимости в равной мере может относиться и к количественным, и к атрибутивным признакам-факторам; группировка по непрерывному признаку производится, как и при построении ряда распределения, путем разбиения области изменения признака на интервалы.

Так как при исследовании зависимости приходится сравнивать распределения по одному признаку групп, образованных по другому признаку, то исследование, в конечном счете, сводится к сопоставлению численностей групп, образованных сразу по обоим признакам, т. е. к анализу результатов комбинационных группировок. Результаты таких группировок часто сводят в таблицы, получившие название корреляционных.

Применение этих методов иллюстрируется следующим примером.

Пример. Исследуется зависимость годности изделий от способа обработки. Из 10000 испытанных изделий 7000 оказались годными, 3000 было забраковано. С другой стороны, известно, что 3000 из испытанных изделий было изготовлено способом А, 7000 — способом Б. Эти цифры, разумеется, не дают возможности судить о том, зависит или не зависит годность изделий от способа обработки, поскольку неизвестно, каким образом годные и бракованные изделия распределены по способам обработки. Рассмотрим следующие возможные случаи:

Случай 1. Результаты комбинационной группировки приведены в таблице 2.1.

Таблица 2.1. Распределение изделий по способам обработки

и годности (случай 1)

Способ обработки	Количество изделий
	годных	бракованных	всего
А	–	3000	3000
Б	7000	–	7000
Всего	7000	3000	10000

В этом случае связь между годностью изделий и способом обработки, очевидно, существует и носит функциональный характер: все изделия, изготовленные способом А, бракованные; все изделия, изготовленные способом Б, — годные.

Случай 2. Результаты комбинационной группировки имеют следующий вид (таблица 2.2):

Таблица 2.2. Распределение изделий по способам обработки

и годности (случай 2)

Способ обработки	Количество изделий
	годных	бракованных	всего
А	2100	900	3000
Б	4900	2100	7000
Всего	7000	3000	10000

Для того, чтобы выяснить, зависит ли годность изделий от способа обработки, необходимо сопоставить распределения изделий, изготовленных разными способами, по годности. Так как разными способами изготовлено различное число изделий, для сопоставления необходимо перейти к относительным единицам (таблица 2.3).

Таблица 2.3. Доли годных и бракованных изделий

при различных способах обработки (случай 2)

Способ обработки	Процент от общего числа изделий, обработанных данным способом
	годных	бракованных	всего
А	70	30	100
Б	70	30	100
Всего	70	30	100

В этом случае годность не зависит от способа обработки.

Дадим количественную формулировку критерию независимости. Пусть N_i· — частота i-го значения признака x; N_·j — частота j-го значения признака y; N_ij — частота сочетания i-го значения признака x и j-го значения признака y; N — объем совокупности. Если признак y не зависит от x, то распределение по y группы, соответствующей любому значению x_i, совпадает с распределением по y всей совокупности. Следовательно, доля элементов, обладающих значением y_j признака y в группе x_i, должна совпадать с долей элементов, обладающих тем же значением признака y по всей совокупности, т.е.

.

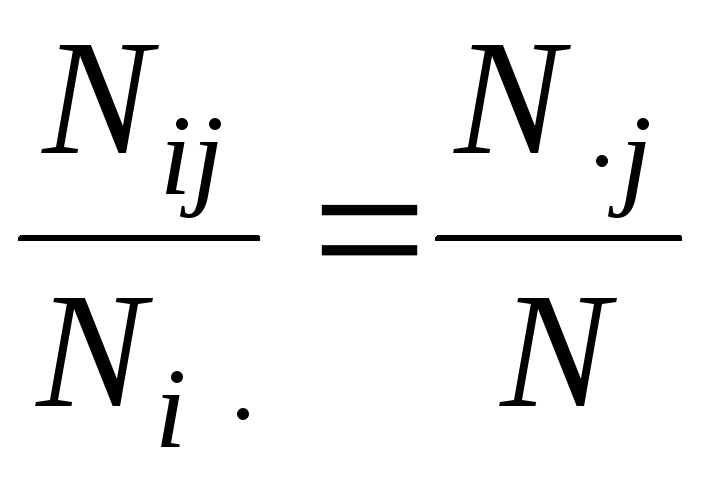Этому равенству можно также придать иную форму:

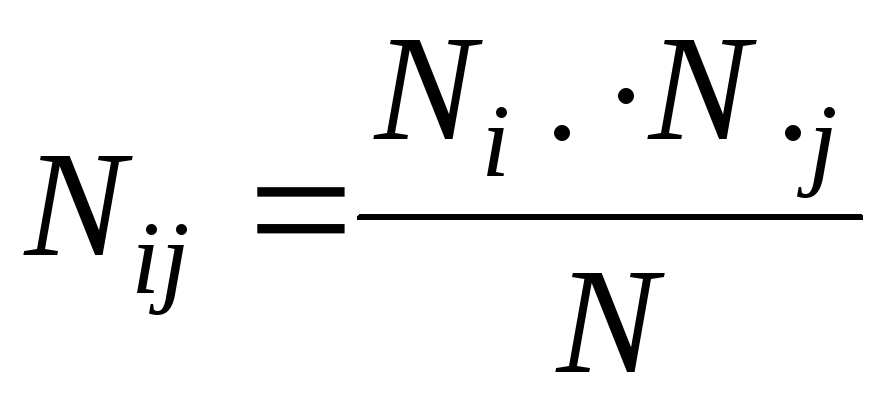. (2.1)

Условием независимости признаков является выполнение равенства (2.1) во всех внутренних клетках корреляционной таблицы; если хотя бы в одной клетке это равенство нарушается, признаки зависимы.

Заметим, что признаки x и y входят в равенство (2.1) симметрично. Отсюда следует, что статистическая зависимость обладает свойством взаимности: если y зависит от x, то и x зависит от y, и обратно.

В рассматриваемом случае равенство (2.1) выполняется во всех клетках корреляционной таблицы 2.2, т.е. частота любой комбинации признаков равна произведению итогов по строке и по столбцу, деленному на объем совокупности.

Случай 3. Комбинационная таблица имеет следующий вид (таблица 2.4):

Таблица 2.4. Распределение изделий по способам обработки

и годности (случай 3)

Способ обработки	Количество изделий
	годных	бракованных	всего
А	2500	500	3000
Б	4500	2500	7000
Всего	7000	3000	10000

Для выяснения факта зависимости, воспользуемся критерием (2.1). Равенство нарушается во всех клетках таблицы; так, для годных изделий, изготовленных по способу А:

,

следовательно, признаки взаимозависимы. В отличие от случая 1 связь здесь носит не функциональный, а статистический характер.

Этот же подход позволяет определить направление действия зависимости. Частоты N_i· и N_·j дают возможность определить число элементов совокупности, которые обладали бы сочетанием значений признаков (x_i, y_j) в случае независимости. Это количество равно

.

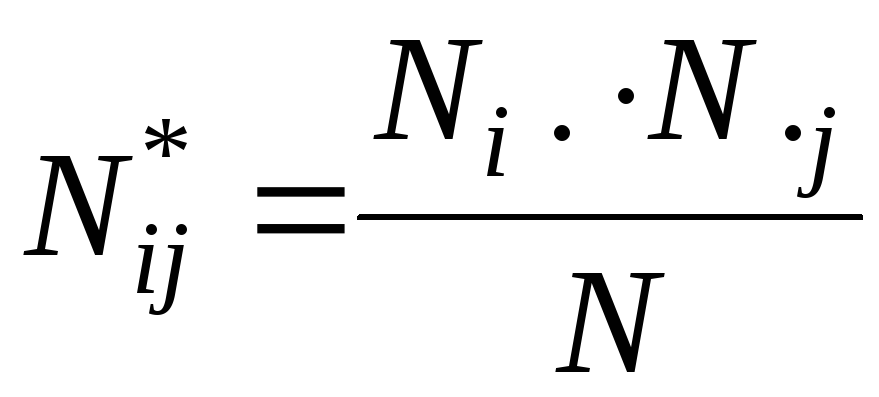Фактическая численность элементов, обладающих этими значениями признаков, равна f(x_i,y_j) и может отличаться от f_ij как в большую, так и в меньшую сторону. Так как это отличие объясняется наличием зависимости, то по знаку неравенства

N_ij

судят о направлении зависимости.

В разбираемом случае имеют место следующие соотношения:

способ А, годные:	;
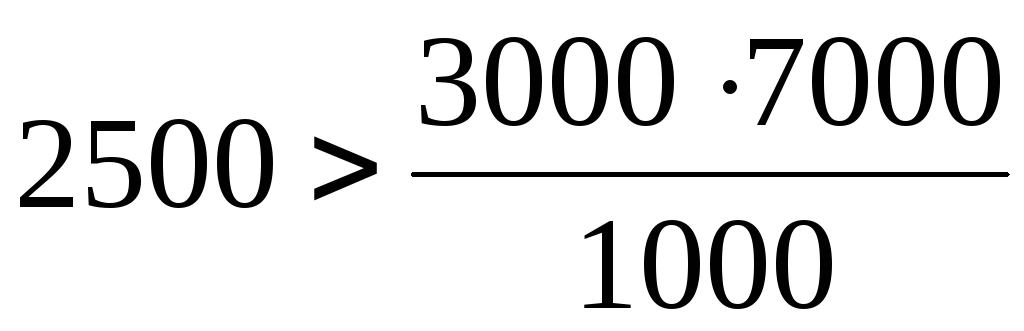способ А, бракованные:	;
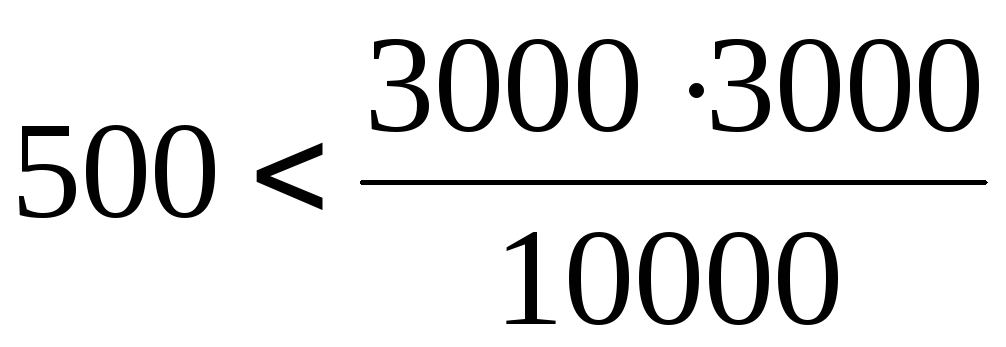способ Б, годные:
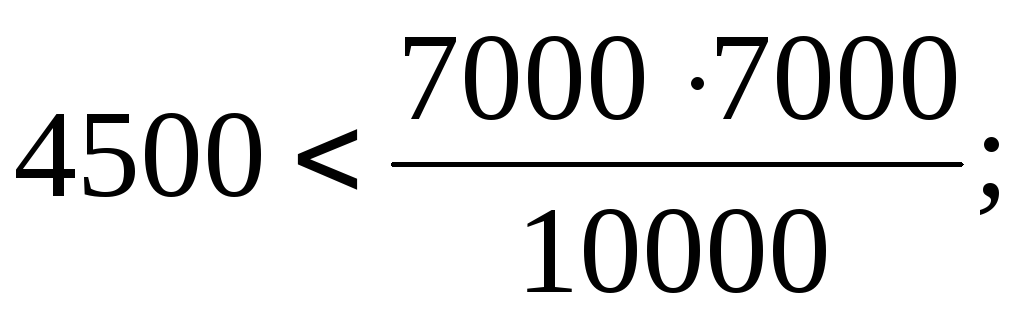
способ Б, бракованные:	.

Эти соотношения представлены в таблице 2.5, в которой знаками обозначено направление действия зависимости: «» — увеличение численности (по сравнению с независимостью), «–» — ее уменьшение.

Таблица 2.5. Направление зависимости

Способ обработки	Изделия
	годные	бракованные
А	+	–
Б	–	+

Следует заметить, что определяемая описанным образом зависимость может не носить закономерного характера. При небольшом числе наблюдений отклонения фактических частот от тех, которые теоретически наблюдались бы при независимости, могут объясняться случайными причинами. Поэтому сравнительно небольшие отклонения при небольшом числе наблюдений можно не принимать в расчет. Методы математической статистики позволяют делать обоснованные выводы о том, является ли обнаруженная зависимость закономерной или же может быть объяснена случайными отклонениями.

Кроме того, статистические методы анализа взаимосвязи не вскрывают причинно-следственного механизма зависимости. Действительно, зависимость обладает свойством взаимности и поэтому невозможно определить, что является причиной, а что — следствием. Кроме того, оба рассматриваемых признака могут принимать различные значения под действием некоторой третьей причины.