§ 11. Замена переменных в уравнениях регрессии

Все рассмотренные выше системы нормальных уравнений были линейными системами относительно неизвестных параметров уравнений регрессии (хотя сами уравнения регрессии были как линейными, так и нелинейными, например, в § 9). В подобных случаях параметры регрессии всегда могут быть определены точными методами.

Однако в некоторых случаях приходится сталкиваться с регрессиями такого вида, что система нормальных уравнений слишком сложна для решения. Например, для степенной функции

с параметрами A и B частные производные равны

и система нормальных уравнений принимает вид:

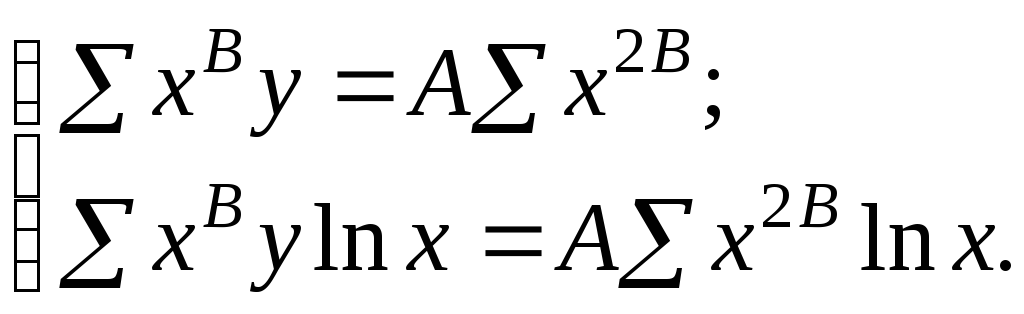
Такая система не может быть решена относительно A и B элементарными методами. Разумеется, она может быть решена численными методами с нужной степенью точности. Однако при этом оказывается невозможным применение тех инструментов анализа, которые описаны выше.

Эта сложность может быть преодолена линеаризацией регрессии — заменой переменных, сводящей поставленную задачу к нахождению линейной регрессии. При этом решение существенно упрощается. Кроме того, появляются возможности использовать при исследовании нелинейных зависимостей тот аналитический аппарат, который был выше рассмотрен применительно к системе линейных связей, — одновременно с нахождением параметров регрессии оценить тесноту связи, разделить непосредственные и косвенные влияния и т. д.

Рассмотрим степенную функцию нескольких переменных:

Логарифмируя обе части полученного выражения и вводя новые переменные

(11.1)

мы придем к линейной множественной регрессии:

Методы определения коэффициентов регрессии и свободного члена, который здесь обозначен , подробно рассмотрены в предыдущем параграфе.

Аналогичным образом может быть преобразована и показательная функция вида

Логарифмируя обе части этого равенства и вводя обозначения

, (11.2)

мы снова придем к линейному уравнению

с коэффициентами, получившими здесь обозначения log A, log B₁, log B₂, …, log B_n.

Так как расчет линейных регрессий представляет собой стандартную операцию, то к замене переменных и приведению регрессии к линейному виду часто прибегают даже в тех случаях, когда коэффициенты могут быть определены непосредственно из системы нормальных уравнений. Так, например, имея функцию регрессии в виде полинома степени n

можно ввести замену переменных

u_i  xⁱ, (11.3)

приводящую регрессию к линейному виду:

Следует отметить, что уравнение, полученное заменой переменных, будет соответствовать принципу наименьших квадратов только в тех случаях, когда результативный признак не заменяется другой переменной. Например, отклонения и не связаны однозначно друг с другом. Поэтому решение, доставляющее минимум среднему квадрату отклонений логарифмов, строго говоря, не должно приводить к минимуму среднего квадрата отклонений самого результативного признака. Тем не менее, если расчетные значения логарифмов функции регрессии близки к соответствующим фактическим значениям логарифма результативного признака, то и сами эти значения — фактическое и регрессионное — мало отличаются друг от друга.

Более того, применение критерия наименьших квадратов к логарифму результирующей переменной (так называемый логарифмический МНК) может оказаться предпочтительнее «строгого» МНК. Дело в том, что разность логарифмов есть логарифм отношения, и если результирующая переменная изменяется в широких пределах, то минимизация относительных отклонений в форме обычно представляет больший интерес, чем минимизация разностей .

Если же заменяются только признаки-факторы, то регрессия строго соответствует критерию наименьших квадратов, так как и в исходном, и в преобразованном уравнениях отыскиваются коэффициенты, обращающие в минимум средний квадрат отклонения . Таким образом, в рассмотренных степенном и показательном уравнениях замена переменных приводит к решению, отличающемуся от точного результата, отвечающего критерию наименьших квадратов, так как результирующая переменная заменяется [равенства (11.1) и (11.2)]; замена переменных для полинома (11.3) приводит к уравнению, строго соответствующему методу наименьших квадратов.

Рассмотрим пример. В таблице 11.1 приведены результаты наблюдения, в ходе которого фиксировались значения признаков x и y. Вид корреляционного поля приведен на рис. 11.1. Качественный анализ требует, чтобы значение при x  0 равнялось нулю. Поэтому зависимость ищется в виде степенной функции

Таблица 11.1. Расчет параметров степенной регрессии

№ наблюдения	x	y	u0 = ln x	u1 = ln y		u0u1
I	1	0.8	0.000	– 0.223	0.000	0.000
II	2	2.0	0.693	0. 693	0.480	0. 481
III	3	4.5	1.099	1.504	1.207	1.652
IV	4	6.2	1.386	1.825	1.922	2.529
V	5	11.1	1.609	2.407	2.590	3.874
Сумма			4.787	6.206	6.199	8.536

Система нормальных уравнений для B и ln A:

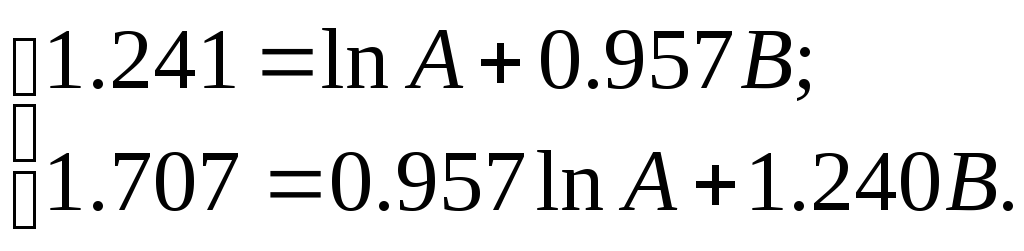
Отсюда ; регрессия представляет собой следующую функцию:

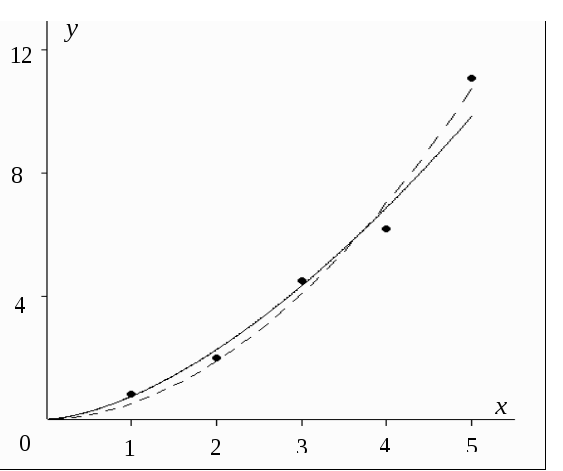
Рис. 11.1

График этой функции построен на корреляционном поле (сплошная линия на рис.11.1). Там же для сравнения построен график функции

определенной численно методом наименьших квадратов (штриховая линия).