Элементы алгебры логики высказывания

Алгебра логики — это раздел математической логики, значение всех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1. Алгебра логики оперирует с логическими высказываниями.

Высказывание — повествовательное предложение, про которое в определенном контексте можно сказать одно из двух истинно оно или ложно. (К высказываниям не относится вопросительные, восклицательные предложения и т.д.)

При этом считается, что высказывание удовлетворяет закону исключенного третьего, то есть каждое высказывание или истинно, или ложно, и не может быть одновременно и истинным и ложным.

Понятие высказывания является одним из исходных понятий математики, которые, как мы знаем, не определяются, а только поясняются через синонимы.

Пример:

1. 5-натуральное число.

2. Новгород – столица России.

3. Высказывания обозначают буквами латинского алфавита:

A, B, C, a, b, c…

4. «Вашингтон — столица США» — истинное утверждение;

5. «Частное от деления 10 на 2 равно 3» — ложное утверждение.

6. Истину и ложь называют логическими значениями высказывания.

В алгебре логики все высказывания обозначают буквами а, b, с и т. д. Содержание высказываний учитывается только при введении их буквенных обозначений, и в дальнейшем над ними можно производить любые действия, предусмотренные данной алгеброй. Причем если над исходными элементами алгебры выполнены некоторые разрешенные в алгебре логики операции, то результаты операций также будут элементами этой алгебры.

Операции над высказываниями

Над высказываниями определены следующие операции: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.

Логической функцией называется функция, которая может принимать только 2 значения – истина или ложь (1 или 0). Любая логическая функция может быть задана с помощью таблицы истинности. В левой ее части записываются возможные наборы аргументов, а в правой – соответствующие им значения функции.

Отрицанием (Инверсией) высказывания А называется новое высказывание «не А» и обозначают его , которое считают истинным, когда Ф- ложно и ложным, когда А – истинно.

Зависимость логического значения от А можно записать в виде таблицы истинности, где 1 обозначает истинность высказывания, а 0-ложность высказывания (Табл.1).

Таблица 1

Таблица истинности отрицания высказывания

А
1	0
0	1

В ЭВМ операция инверсии физически реализуется стандартным логическим элементом «не» – инвертором.

    

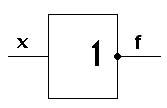
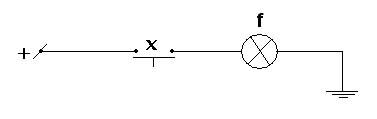
Конъюнкцией двух высказываний А и В называется новое высказывание «А и В», обозначаемое А&В (или А^В), которое считают истинным, если оба высказывания одновременно истинны, и ложным, если хотя бы одно из них ложно.

Зависимость логического значения А&В от логических значений А и В можно записать в виде таблицы истинности (Табл.2).

Таблица 2

Таблица истинности конъюнкции двух высказываний

А	В	А&В
1	1	1
1	0	0
0	1	0
0	0	0

Функция конъюнкции истинна тогда, когда истинны одновременно оба высказывания.

В ЭВМ операция конъюнкции физически реализуется стандартным логическим элементом «и» - конъюнктером.

    

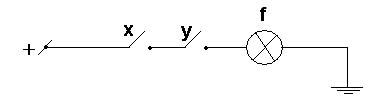
Дизъюнкцией двух высказываний А и В называется новое высказывание «А или В», обозначаемое АВ, которое считают истинным, если истинно хотя бы одно из входящих в него высказываний и ложным, если ложны оба высказывания. Зависимость логического значения АВ от логических значений А и В можно записать в виде таблицы истинности (Табл.3).

Таблица 3

Таблица истинности дизъюнкции двух высказываний

А	В	АВ
1	1	1
1	0	1
0	1	1
0	0	0

Функция дизъюнкции истинна тогда, когда истинно хотя бы одно из входящих в него высказываний.

В ЭВМ операция дизъюнкции физически реализуется стандартным логическим элементом «или» - дизъюнктером.

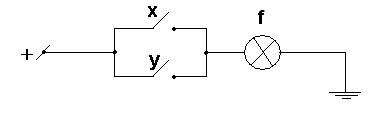
Импликацией двух высказываний А и В называют новое высказывание «если А, то В», обозначаемое А→В, которое считают ложным, если А-истинно, а В – ложно и истинным во всех остальных случаях (Табл.4).

Таблица 4

Таблица истинности импликации двух высказываний

А	В	А→В
1	1	1
1	0	0
0	1	1
0	0	1

В ЭВМ нет логического элемента, который реализует операцию импликации. Для реализации данной операции строиться комбиноторно - логическая схема. На основании таблицы истинности составляется булева функция (СДНФ – совершенная дизъюнктивная нормальная форма)

Выписываем те строчки, где имеются 1 на выходе. Для всех таких наборов переменных запишем конъюнкции, инвертируя те переменные, которым соответствуют 0. Объединим полученные конъюнкции знаком дизъюнкции.

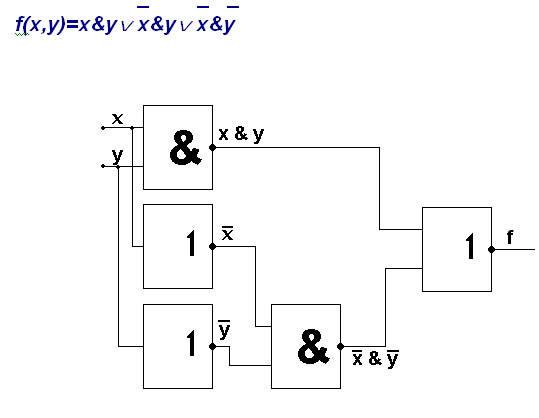
    Анализируя, видим, что схема сложна и возникает желание упростить ее. Упрощение двоичных функций называется минимизацией.

 Будем упрощать аналитически, используя закон логического склеивания.

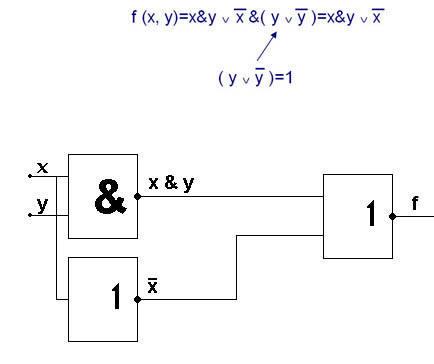
Эквиваленцией двух высказываний А и В называется новое высказывание «А тогда и только тогда, когда В», обозначаемое А↔В, которое считают истинным, если А и В имеют одинаковые значения истинности и ложным в противоположном случае.

Соответствующие выражения языка (Х эквивалентно Y, Х необходимо и достаточно для Y, Х тогда и только тогда, когда Y,   Х если и только Y, Х такое же, как и Y) (Табл. 5).

Таблица 5 

Таблица истинности эквиваленции

А	В	А↔В
1	1	1
1	0	0
0	1	0
0	0	1

В ЭВМ нет логического элемента, который реализует операцию эквивалентности. Для реализации данной операции строиться комбинаторно - логическая схема. На основании таблицы истинности составляется булева функция (СДНФ – совершенная дизъюнктивная нормальная форма). 

Выписываем те строчки, где имеются 1 на выходе. Для всех таких наборов переменных запишем конъюнкции, инвертируя те переменные, которым соответствуют 0. Объединим полученные конъюнкции знаком дизъюнкции.

                                  

Минимизацию двоичной функции произведем на основании закона де Моргана.

        

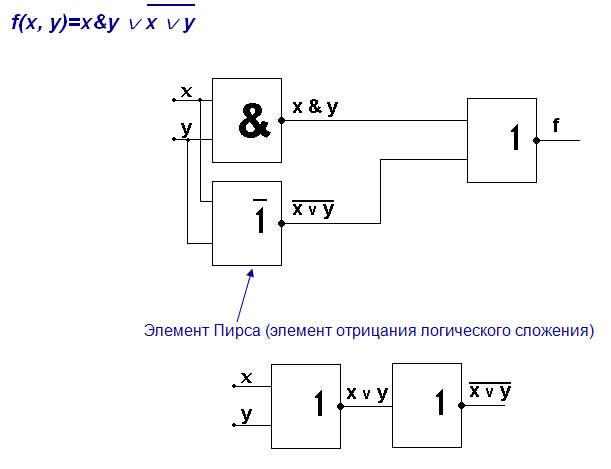
Сводная таблица истинности для различных операций имеет следующий вид (Табл.6).

Таблица 6

Таблица истинности для различных операций

А	В		А&В	АВ	А→В	А↔В
1	1	0	1	1	1	1
1	0	0	0	1	0	0
0	1	1	0	1	1	0
0	0	1	0	0	1	1

Сложным высказыванием называется высказывание, полученное из простых высказываний с помощью логических операций.

Соглашения, принятые для упрощения записи сложных высказываний:

1. все высказывание в скобки не заключается.

2. не заключается в скобки часть высказывания, стоящая под знаком отрицания.

3. установлен следующий порядок действий первым выполняется отрицание, затем конъюнкция, далее дизъюнкция, импликация и эквиваленция.

Сложные высказывания называют равносильными, если при любом наборе логических значений они имеют одинаковые таблицы истинности.

Пример 1. Упростить формулу