3 Средние скорости молекул

Пользуясь функцией распределения М., можно вычислить ряд важных в молекулярной физике величин: средней арифметической скорости <v>, средней квадратичной скорости v = √<v²> и наиболее вероятной скорости v_н.

1. Средняя арифметическая скорость <v> по определению равна отношению суммы скоростей всех молекул единицы объема к числу молекул единицы объема.

Число молекул в единице объема dn_v, скорости которых заключены в интервале от v до v+dv равно nf(v)dv; Сумма скоростей всех таких молекул равна vnf(v)dv. Чтобы найти сумму скоростей всех молекул, обладающих любыми скоростями, нужно это выражение проинтегрировать по всем возможным значениям скорости от 0 до ∞. Следовательно, сумма всех скоростей молекул ∫vnf(v)dv, а <v> = 1/n∫ vnf(v)dv , т.е.,

∞

0

∞

0

∞

0

<v> = ∫vf(v)dv , подставив f(v), получим:

∞

0

<v> = 4/√π (m/2kT)^3/2∫ v³e dv = 4/√π (m/2kT)^3/2∫ v²e vdv

vdv = d(v²)/2, значит <v> = 4/√π (m/2kT)^3/2½∫ v²e d(v²)

Введем новую переменную Z=mv²/2kT : ½∫ v²e d(v²) = ½ (2kT/m)²∫Ze^-ZdZ, тогда, учитывая, что ∫Ze^-ZdZ =1, получим:

<v> = 4/√π (m/2kT)^3/22(kT/m)² = √8kT/πm

2) Средняя квадратичная скорость √<v²> – отношение суммы квадратов скоростей молекул единицы объема к числу молекул в этом объеме:

<v²> = ∫ v²f(v)dv = 4π(m/2πkT) ^3/2∫ v⁴e dv

берется по частям ∫ v⁴edv = 3/8(2kT/m)^5/2√π

тогда <v²> = 3kT/m; = √<v²> = √3kT/m

3)Наиболее вероятная скорость молекулы, ей соответствует max на кривой распределения М., поэтому ее находят, приравнивая производную функции нулю:

(d/dv)f(v) = d/dv[4/√π (m/2kT)^3/2v²e ] = 0

т.е. d/dv(v²e ) = 0, после дифференцирования получаем:

2ve(1-mv²/2kT) = 0. Это уравнение имеет три решения: v = 0; v = ∞, либо выражение в скобках равно нулю. Следовательно, v_н находят из условия:

1- mv²/2kT = 0 => v_н = √2kT/m

Сравнивая выражения для <v>, v и v_н, видно, что

v_{ср. кв.} = √3π/8<v> = 1,13<v> = √3/2 v_н = 1,22v_н

т.е. и средняя арифметическая, и средняя квадратичная скорости близки к v_н.

Б21

1. Закон сохранения механической энергии частицы.

2. Преобразования Лоренца.

4. Обратимые и необратимые термодинамические процессы.

1. Закон сохранения механической энергии частицы.

Из выражения следует, что в стационарном поле консервативных сил полная механическая энергия частицы может изменяться под действием только сторонних сил, отсюда вытекает закон сохранения механической энергии частицы.

Если сторонние силы отсутствуют, то полная механическая энергия частицы в стационарном поле консервативных сил остается постоянной.

;

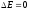Закон сохранения позволяет решать многие вопросы, не привлекая уравнения движения, которые часто приводят к ??? расчетам.

3. 1 Обратимые и необратимые процессы

Для расширения представлений о термодинамических процессах уточним понятие обратимого процесса: процесс, совершаемый системой наз. обратимым, если после него можно возвратить систему и все тела, взаимодействующие с ней, в их начальное состояние таким образом, чтобы в других телах не возникало каких-либо остаточных изменений.

Необходимое условие обратимости терм. процесса – его равновесность, т.е. всякий обратимый процесс всегда является равновесным (квазистат). Однако не всякий равновесный процесс является обратимым. Например, квазистататический процесс равномерного движения по поверхности под действием силы тяжести и трения – процесс необратимый.

Пример обратимого процесса – незатухающие колебания тела, подвешенного на пружине в вакууме. Система тело-пружина консервативна. Ее механические колебания не вызывают никаких изменений в энергии теплового движения частиц системы. Изменение состояния системы связано с изменением ее конфигурации и скорости движения тела, которые полностью повторяются через период.

Пример необратимого процесса – торможение тела под действием силы трения. Если сила трения единственная сила, то скорость тела уменьшается и оно останавливается. При этом энергия мех движ. тела, как целого уменьш. и расходуется на увел. энергии тепл. движ. частиц тела и среды. Другими словами, за счет нач. кинет. эн. тела (W_к) растет внутрення энергия U тела и среды, нагревающихся при трении ΔU = W_к. Этот прямой процесс протекает самопроизвольно, он идет без каких либо процессов, происходящих с окружающими телами. Но для осуществления обратного процесса возвращения системы в исходное состояние необходимо, чтобы остановившееся тело вновь пришло в движение за счет энергии, выделившейся при его охлаждении и окружающей среды. Известно, что хаотическое движение тела, т.е., U не может самопроизвольно привести к упорядоченному движению всех частиц тела, как целого. Для реализации этого необходим дополнительный, так называемый компенсирующий процесс. Он заключается в охлаждении тела и окружающей среды до первоначальной Т, т.е., в отдаче ими некоторому другому телу теплоты Q = W_к и в совершении над рассматриваемым телом работы, равной W_к. Поэтому, хотя в результате прямого и обратного процесса система тело-среда возвратилась в исходное состояние, состояние внешних тел изменяется (меняется Т, затем совершается работа, т.е. меняются координаты). Следовательно, процессы сопровождающиеся трением необратимы.

Процесс теплообмена между двумя телами с разной Т приводит к выравниванию средних энергий тепл. движения частиц обоих тел. Энергия частиц более нагретого тела уменьшается, менее нагретого – увеличивается. В итоге Т₁ = Т₂. Процесс идет самопроизвольно, как только обеспечен контакт между телами. Обратный процесс – нагревание одного тела за счет охлаждения другого, имевшего вначале Т₁ = Т₂, самопроизвольно не протекает. Для него используется холодильное устройство, работа которого приводит к изменению состояния других внешних тел. Значит процесс теплообмен при конечной ΔТ является необратимым. Можно показать, что необратимыми являются процессы диффузии и растворения.

Из всех этих примеров необратимых процессов можно сделать общие выводы: Все они в прямом направлении происходят самопроизвольно, а для осуществл. обр. проц. требуется одновременное протекание компенсирующих процессов. Все реальные процессы идут с конечной скоростью и сопровождаются трением и теплообменом при конечной разности температур тел, находящихся в тепловом контакте, значит все реальные процессы, строго говоря, необратимы. Однако в некоторых случаях условия протекания процесса таковы, что их приближенно можно считать обратимыми.

Б-22

1. Кинематика вращательного движения: угол поворота, угловая скорость, угловое ускорение, связь между линейной и угловой скоростью.

2. Релятивистский импульс. Основное уравнение релятивистской механики.

3. Энтропия. Энтропия идеального газа.

1. Кинематика и динамика вращательного движения.

Поворот тела на некоторый угол можно задать в виде отрезка длина которого , а направление совпадает с осью вращения и определяется правилом правого винта: Направление должно быть таким, чтобы глядя вдоль него, мы видели поворот совершающийся по часовой стрелке.

При поворотах на очень малые углы, путь проходимый точкой можно считать прямолинейным, поэтому два последовательных малых поворота и 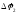(вокруг разных осей, оси в данном случае) обуславливают как видно из рис., такое же перемещение, любой точки тела, как и поворот получаемый из и 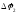сложением о правилу параллелограмма. Значит очень малые повороты можно рассматривать как векторы. Направление вектора поворота , связывается с направлением вращения тела, следовательно не является истинным вектором, а является псевдовектором.

Векторная величина называется угловой скоростью тела направлена вдоль оси вращения, в сторону, определяемую правилом правого винта — тоже псевдовектор, модуль , если — равномерное вращение , для равномерного движения -угол поворота в единицу времени. период вращения число оборотов , а .

Понятия и можно сохранить и для неравномерного вращения, понимая под ними мгновенное вращение.

Вектор может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве ( по направлению). Если за получает приращение то изменение угловой скорости со временем характеризуется угловым ускорением

— тоже псевдовектор.

Точки вращающегося тела имеют разные линейные скорости, которые определяют и . Если за тело повернулось на , то . Линейная скорость точки 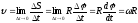; т.е. .

Найдем связь между векторами и . Положение для модулей точки определяет . Из рис. видно, что совпадает с по направлению, модуль 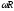равен .

Модуль нормального ускорения точек или через .

Когда ось вращения не поворачивается в пространстве, тогда тангенциальное ускорение:

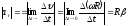; -модуль угловой скорости, т.е .

Т.о. нормальное и тангенциальное ускорение растут пропорционально .

3. Энтропия (от греческого слова преобразовать, превращать)

В середине ХІХ века было сделано существенное открытие, касающееся обратимых т. процессов. Это открытие связано с именами Карно и Клаузиуса и является существенной частью 2-го закона термодинамики.

Оказалось, что наряду с внутренней энергией у тела имеется еще одна важная функция состояния – энтропия. Так же, как и внутренняя энергия, энтропия определяется с точностью до произвольной постоянной. В опытах проявляется значение разности энтропий.

Если тело или система при бесконечно малом переходе из одного состояния в другое при температуре Т получает малое количество теплоты δQ, то отношение δQ/Т является полным дифференциалом некоторой функции S. Эта функция и есть энтропия, определяющаяся, таким образом равенством:

dS = δQ/Т, при малом переходе,

а для конечного изменения: ΔS = S₂-S₁ = δQ/Т

Сущность энтропии заключается в следующем: Переход системы из одного состояния в другое может произойти бесчисленным количеством способов (разные кривые на графике с окончанием в одних точках) При этих переходах тело может получать разные количества тепла, однако во всех случаях интеграл будет иметь одинаковое значение, т.е., не зависит от вида перехода, а определяется только состояниями системы в точках 1 и 2. Значит S является функцией состояния.

2

1

Например, тело нагревают равномерно от 20 до 25˚С, при этом оно получает по 5 Дж теплоты на 1 К. Тогда прирост энтропии, примерно, равен S₂-S₁ ≈ 5/293,5+5/294,5+5/295,5+5/296,5+5/297,5 Дж/К.

Наиболее просто выразить изменение энтропии при изотермическом процессе: S₂-S₁ = =Q/Т, т.к., Т = const. Пример: при таянии 1 кг льда

Дж/К.

За нуль энтропии может быть принято значение энтропии любого состояния, (кипящей воды, плавящегося льда). Однако, в некоторых случаях за нуль принимают значение энтропии при абсолютном нуле Т. Приняв S = 0 при Т = 0, энтропию при произвольной температуре находят из выражения:

2

1

S = νС_рdT/T если нагрев происходил при р= const. Чтобы определение энтропии dS = δQ/Т было обоснованным, необходимо доказать, что в любом обратимом круговом процессе интеграл от δQ/Т тождественно равен 0.

δQ/Т ≡0, т.е. S = const

Если известно уравнение состояния вещества, то энтропия (с точностью до const) может быть вычислена весьма просто. По определению:

dS = δQ/Т , подставив сюда δQ из 1-го з-на т. получим:

dS = (m/M)(C_vdT/T+RdV/V)

Взяв определенный интеграл, получим

S₂-S₁ = (m/M)(C_v lnT₂ /T₁+ RlnV₂/V₁).

Это выражение для энтропии идеальных газов: она возрастает с повышением Т и при увеличении объема газа при подводе к нему теплоты δQ.

Б-23

1. Нормальное ускорение и модуль тангенциального ускорения при вращении.

2. Кинетическая энергия релятивистской частицы.

3. Принцип возрастания энтропии. Примеры: при теплообмене, при расширении в вакуум, при механическом движении в сосуде с газом.

1. Вектор может изменяться как за счет изменения скорости вращения оси (по величине), так и за счет поворота оси вращения в пространстве ( по направлению). Если за получает приращение то изменение угловой скорости со временем характеризуется угловым ускорением

— тоже псевдовектор.

Точки вращающегося тела имеют разные линейные скорости, которые определяют и . Если за тело повернулось на 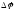, то 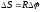. Линейная скорость точки ; т.е. .

Найдем связь между векторами и . Положение для модулей точки определяет . Из рис. видно, что совпадает с по направлению, модуль равен .

Модуль нормального ускорения точек или через .

Когда ось вращения не поворачивается в пространстве, тогда тангенциальное ускорение:

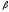; -модуль угловой скорости, т.е .

Т.о. нормальное и тангенциальное ускорение растут пропорционально .

3. Принцип возрастания энтропии

Необратимость всех реальных процессов в конечном счете связана с тем, что в каждом из них присутствует один из самопроизвольных процессов. В реальных явлениях невозможно избежать ни самопроизвольного расширения, ни трения, ни теплового рассеяния. Во всем этом есть один общий признак. Он состоит в том, что во всех самопроизвольных процессах энтропия возрастает.

Примеры:

а) При теплообмене между двумя телами с разными температурами общее изменение энтропии равно:

S₂-S₁ = Q₁/Т₁+ Q₂/Т₂, где Q₁ – тепло полученное, холодным телом; Q₂ – тепло, отданное горячим телом.

т.к. Т₂> Т₁ то Q₁ = - Q₂>0 - тепло, отданное телом, считается <0, тогда S₂-S₁ = Q₁(1/ Т₁-1/ Т₂)>0, т.е., при теплообмене общая энтропия системы возрастает.

б) Если внутри сосуда с газом происходит интенсивное механическое движение (вертится колесо), то температура газа за счет внутреннего трения растет (при этом V = const), поэтому энтропия системы изменится: S₂-S₁ = (m/M)(CvlnT₂/T₁), т.е., снова возрастает.

в) При расширении газа в пустоту при Т = const приращение энтропии: S₂-S₁ = (m/M)(RlnV₂/V₁); опять >0.

Итак, во всех самопроизвольных процессах энтропия системы возрастает. Это имеет важное значение для необратимых процессов.

Для обратимых процессов прирост энтропии был бы равен dS = δQ/T; Т.к. каждый необратимый процесс сопровождается самопроизвольными явлениями, идущими с повышением энтропии, то приращение энтропии при сообщении δQ для них будет выше, чем приращение, которое имело бы место при обратимом процессе, т.е. dS ≥ δQ/T.

Если система теплоизолирована (адиабатный процесс), то δQ = 0 и это утверждение имеет вид:

dS = 0, S = const для обратимых процессов и

dS > 0 (для необратимых);

т.е., в теплоизолированных системах возможны только процессы с возрастанием энтропии, или с ее сохранением.

Если в предыдущие формулы ввести вместо знака равенства знак ≥, то закон возрастания энтропии запишется как для обратимых, так и для необратимых процессов:

dS ≥ δQ/T (для обратимых знак =, для необратимых знак >).

Эта ф-ла передает содержание 2-го закона т.

Можно объединить 1 и 2 з-ны т. и записать их в виде: dS ≥ (dU+pdV)/T

Принцип возрастания энтропии относится к закрытым системам. Если же система общается с внешней средой, т.е. она открыта, то энтропия может и убывать.

Б-24

1. Момент импульса частицы. Момент силы. Уравнение моментов.

2. Связь между массой и энергией в релятивистской механике.

3. Энтропия в необратимых процессах. Энтропия в изолированной системе (адиабатический процесс)

1. момент импульса частицы. Момент силы.

Кроме энергии и импульса существует ещё Одина физическая величина. С которой связан закон сохранения — это момент импульса. Моментом импульса частицы относительно точки О называется вектор 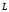равный , 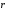-радиус; -импульс.

Т.е. является ??? вектором. Его направление выбрано так, что вращение вокруг О в направлении и вектор образует правовинтовую систему. Модуль  угол между и

плечо вектора относительно О.

Найдем с какой величиной связано изменение вектора во времени:

.

Т.к т.о неподвижна, то равно скорости частицы, т.е. совпадает с 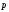, т.е. . Далее — второй закон Ньютона и ; Величина —момент силы аксиальный вектор. , —плечо силы относительно т.О.

Т.о производная по момента импульса частицы, относительно некоторой т.О выбранной системы отсчета равна моменту равнодействующей силы относительно этой точки . Это уравнение называют уравнением моментов.

Если система отсчета является неинерциальной, то в момент силы включает в себя как момент сил взаимодействия, так и момент сил инерции (относительно той же т.О). Из уравнения моментов следует что если , то —равномерное вращательное движение. Т.е. если момент всех сил относительно т.О системы отсчета равен О, в течение интересующего нас , то момент импульса частицы относительно этой точки остается постоянным.

Уравнение моментов позволяет найти точки относительно О в любой момент времени если известна 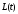частицы относительно точки. Для этого достаточно продифференцировать уравнение . Кроме этого, если известна зависимость , то можно найти приращение момента импульса частицы относительно т.О за любой промежуток времени. Для этого необходимо проинтегрировать уравнение , тогда

Выражение —импульс момента силы подобно , т.е. приращение момента импульса частицы за любой промежуток времени равно импульсу момента силы за э

то время.

3. Для обратимых процессов прирост энтропии был бы равен dS = δQ/T; Т.к. каждый необратимый процесс сопровождается самопроизвольными явлениями, идущими с повышением энтропии, то приращение энтропии при сообщении δQ для них будет выше, чем приращение, которое имело бы место при обратимом процессе, т.е. dS ≥ δQ/T.

Если система теплоизолирована (адиабатный процесс), то δQ = 0 и это утверждение имеет вид:

dS = 0, S = const для обратимых процессов и

dS > 0 (для необратимых);

т.е., в теплоизолированных системах возможны только процессы с возрастанием энтропии, или с ее сохранением.

Если в предыдущие формулы ввести вместо знака равенства знак ≥, то закон возрастания энтропии запишется как для обратимых, так и для необратимых процессов:

dS ≥ δQ/T (для обратимых знак =, для необратимых знак >).

Эта ф-ла передает содержание 2-го закона т.

Можно объединить 1 и 2 з-ны т. и записать их в виде: dS ≥ (dU+pdV)/T

Принцип возрастания энтропии относится к закрытым системам. Если же система общается с внешней средой, т.е. она открыта, то энтропия может и убывать.

Б-25

1. Закон сохранения момента импульса.

2. Центробежная сила инерции.

3. Второй закон термодинамики.

1. Закон сохранения момента импульса системы.

Рассмотрим систему состоящую из 2 частиц, на которые действуют также силы и . Момент импульса является аддитивной величиной. Для системы равен векторной сумме моментов импульса отдельных частиц относительно одной и той же точки .

Нам известно, что —моменту всех сил, действующих на частицу, а изменение момента системы , тогда ; ;

— суммарный момент всех внутренних сил действующих на частицы.

— суммарный момент всех внешних сил действующих на частицы.

Значит для двух частиц:

.

Суммарный момент внутренних сил относительно любой точки равен 0. силы взаимодействия между частицами по 3^му закону Ньютона действуют по одной прямой, значит имеют одинаковое плечо, поэтому момент каждой пары внутренних сил равен 0.

Т.о. ; т.е. системы изменяются под действием внешних сил . Если внешние силы отсутствуют , , то , является аддитивным сохраняющейся величиной. Т.е. момент импульса замкнутой системы частиц остается постоянным, не меняется со временем. Это справедливо относительно любой точки инерциальной системы отсчета: т.е. моменты импульса отдельных частей 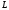одной части системы происходят за счет убыли другой части (относительно одной точки).

Закон справедлив и в неинерциальной системе отсчета в тех случаях когда суммарный момент всех внешних сил, включая силы инерции равен нулю.

Закон играет такую же роль как закон сохранения энергии импульса. Он позволяет решать разные задачи, не рассматривая детально внутренние процессы. Пример: разгоняют????

Момент импульса ; т.е. уменьшается как . Этот эффект широко используют гимнасты, фигуристы и т.д. здесь мы интересуемся силами взаимодействия и т.д. у незамкнутых систем может сохраняться не сам , а его проекция на некоторую неподвижную ось . Это бывает, когда всех внешних сил.

; ;

В физике понятие момента импульса расширяют на немеханические системы (с электромагнитным излучением, в атомах, ядра и др.) где не действуют законы Ньютона. Здесь закон сохранения момента импульса уже не является следствием законов Ньютона, а представляет собой самостоятельный принцип, является обобщением опытных фактов и является одним из фундаментальных законов наряду с законами сохранения энергии и импульса.

3. Второй закон термодинамики

Второй з-н термодинамики состоит в утверждении, что энтропия в теплоизолированной системе возрастает. Существуют и другие формулировки 2-го з-на т. Исторически он вошел в науку в виде постулата Томсона о невозможности создании вечного двигателя второго рода.

Вечным двигателем 1-го рода называют машину, которая создает работу из ничего, вопреки 1 з-ну термодинамики (з-ну сохранения энергии). Вечным двигателем 2-го рода называют такой двигатель, который производит работу при помощи периодически действующей машины за счет одного только отнятия теплоты от окружающей среды, т.е. с η =1. Двигатель 2-го рода это тепловая машина, работающая с нагревателем, но без холодильника. Она могла бы проработать один такт, газ в сосуде с поршнем расширился бы, но на этом работа двигателя закончилась, т.к., для продолжения работы машины часть тепла, полученного газом, необходимо передать холодильнику. Формально, невозможность двигателя 2-го рода видна из ф-лы максимального кпд. При отсутствии теплового перепада Т₂ = Т₁, η = 0; η = (Т₁-Т₂)/Т₁ = 1- Т₂/Т₁.

Невозможно осуществить периодически действующий вечный двигатель, комбинируя изотермическое расширение с процессом адиабатного сжатия. Такой процесс невозможен, даже, если бы его удалось сделать обратимым. При изотермическом расширении тела энтропия S падает. Значит процесс сжатия должен приводить к возрастанию S. Этого однако не может сделать адиабатный процесс (при нем S = const).

Принятой формулировке 2-го з-на т. вполне соответств. также постулат Клаузиуса, который состоит в утверждении о невозможности перехода тепла от менее нагретого тела к более нагретому без компенсации, т. е. без совершения работы внешними силами.

Б-26

1. Вращение тела вокруг неподвижной оси. Момент инерции твердого тела.

2. Теорема Штейнера.

3. Статистический смысл второго закона термодинамики.