
Б-1
Кинематические уравнения движения, траектория, путь.
-
Кинетическая энергия вращающегося тела и работа вращения.
-
Термодинамические системы. Термодинамические параметры и процессы.
3. Равновесное состояние термодинамического процесса, Обратимые и круговые процессы
1. Кинематические уравнения движения.
При
движении т.М ее координаты и
 меняются со временем для задания закона
движения необходимо указывать вид
функциональной зависимости от времени
всех трех её координат, либо
меняются со временем для задания закона
движения необходимо указывать вид
функциональной зависимости от времени
всех трех её координат, либо
 ;
;
 ;
;
 ;
;
 .
Эти уравнения называются кинетическими
уравнениями движения точки.
.
Эти уравнения называются кинетическими
уравнениями движения точки.
Траектория — линия описываемая точкой при ее движении относительно выбранной системы координат. Уравнение траектории можно получить из кинематических уравнений, исключив время. Различают прямолинейное и криволинейное движение плоская траектория, объемная.
Длина
пути расстояние
 ,
пройденное за рассмотренный промежуток
,
пройденное за рассмотренный промежуток
 и изменяемое вдоль траектории в
направлении движения; т.е.
и изменяемое вдоль траектории в
направлении движения; т.е.
 .
.
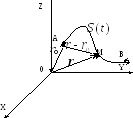
Пусть
точка движется от А к В по криволинейному
пути АВ в начальный момент в т.А ( )
а в
)
а в
 находится в т.М с
находится в т.М с
 ;
S=длина
траектории.
;
S=длина
траектории.
2. Кинетическая энергия вращающегося тела.
Рассмотрим
абсолютно твердое тело, вращающееся
вокруг неподвижной оси, проходящей
через него. Разобьем его на частицы с
малыми объемами и массами
 ,
,
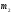 ….
находящиеся на расстояние
….
находящиеся на расстояние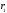 ,
,
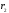 … от оси вращения. Разным
… от оси вращения. Разным
 будут соответствовать, разные
будут соответствовать, разные
 ,
,
 … кинетическая энергия вращения всего
тела сложится из энергий составляющих
его частицу
… кинетическая энергия вращения всего
тела сложится из энергий составляющих
его частицу 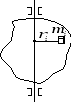
 т.к.
т.к.
 всех частиц одинакова, то
всех частиц одинакова, то
 ,
,
 … тогда
… тогда
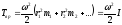 т.е.
т.е.

Формула
справедлива для тела. которое вращается
вокруг неподвижной оси. Если тело катится
(шар, колесо, и т.д.), то энергия движения
складывается из энергии вращения и
энергии поступательного движения, т.е.
для тела массой
 ,
моментом инерции
,
моментом инерции
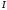 ,
скоростью поступательного движения
,
скоростью поступательного движения
 и вращения
и вращения

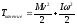 ;
;
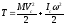 ;
;
формула справедлива для произвольного движения, поскольку его можно разложить на совокупность вращения относительно оси инерции и поступательного движения.
Работа вращения тела.
Если
тело приводится во вращение силой
 ,
то его вырастает на величину затраченной
работой. Также как и в поступательном
движении эта работа зависит от
,
то его вырастает на величину затраченной
работой. Также как и в поступательном
движении эта работа зависит от
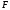 и произведено перемещение. Однако
перемещение теперь угловое и выражение
для работы при перемещении материальной
точки неприменимо. Т.к. тело абсолютно
твердое, то работа силы
и произведено перемещение. Однако
перемещение теперь угловое и выражение
для работы при перемещении материальной
точки неприменимо. Т.к. тело абсолютно
твердое, то работа силы
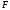 (хотя
она приложена в точке) равна работе,
затраченное на поворот всего тела. При
повороте на угол
(хотя
она приложена в точке) равна работе,
затраченное на поворот всего тела. При
повороте на угол
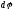 точка приложения силы проходит путь
точка приложения силы проходит путь
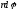 и работа
и работа
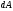 равна произведению проекции
равна произведению проекции
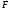 на направление смещения на величину
смещения
на направление смещения на величину
смещения
 ;
;
 ;
;
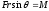 —момент
силы;
—момент
силы;
 —плечо
силы; т.е.
—плечо
силы; т.е.
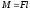

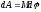 .
Работа вращение идёт на увеличение
кинетической энергии
.
Работа вращение идёт на увеличение
кинетической энергии
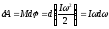 ;
;
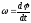 ;
;
 .
.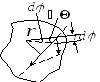
Ось, положение которой в пространстве остаётся неизменным при вращении вокруг неё тела в отсутствии внешних сил (со стороны, например, подшипников) называется свободной осью тела.
Можно
доказать, что для тела любой формы с
произвольным распределением массы
существуют 3 взаимно
 ,
проходящие через центр масс тела оси,
которые могут служить свободными осями;
они называются главными осями инерции
тела.
,
проходящие через центр масс тела оси,
которые могут служить свободными осями;
они называются главными осями инерции
тела.
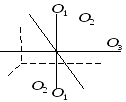
Моменты инерции относительно главных осей называется главным моментом инерции тела.
Для
некоторых тел с надлежащим распределением
масс
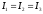 (шар куб и т.д.). Эти тела называются
шаровыми волчками. Характерным для них
является то, что любая ось, проходящая
через С обладает свойствами свободной
оси, и, следовательно, ни одна из главных
осей инерции не фиксирована, как и для
шара.
(шар куб и т.д.). Эти тела называются
шаровыми волчками. Характерным для них
является то, что любая ось, проходящая
через С обладает свойствами свободной
оси, и, следовательно, ни одна из главных
осей инерции не фиксирована, как и для
шара.
Тела с
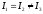 ведут себя как однородные тела вращение
их называют симметричными
волчками.
ведут себя как однородные тела вращение
их называют симметричными
волчками.
3. Термодинамические системы. Термодинамические параметры и процессы
Макросистема, рассматриваемая методами термодинамики, называется термодинамической (т.) системой. Это может быть, например, жидкость и пар, находящийся с ней в равновесии. Система может быть открытой или закрытой (в зависимости от того, обменивается ли она веществом с окружающими телами), изолированной (если нет обмена энергией с внешними телами).
Т. система
может находиться в различных состояниях,
отличающихся физическими величинами
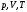 ,
называемых т. параметрами состояния.
Состоянию газа отвечают также определенная
масса и химический состав вещества.
,
называемых т. параметрами состояния.
Состоянию газа отвечают также определенная
масса и химический состав вещества.
Если
параметры т. системы неизменны во времени
и в системе отсутствуют потоки энергии
и вещества, такое состояние т. системы
называют равновесным. В такое состояние
придет тело, если его изолировать от
других тел и предоставить самому себе.
Все его т. параметры (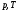 и
др.) через некоторое время примут
одинаковые для всех точек тела значения
– тело перейдет в равновесное состояние.
и
др.) через некоторое время примут
одинаковые для всех точек тела значения
– тело перейдет в равновесное состояние.
Процесс
перехода системы из равновесного
состояния в неравновесное (или наоборот)
называется релаксацией. Время, в течение
которого физическая величина, возвращаясь
в равновесное состояние, изменяется в
 раз,
называется характеристическим временем
релаксации.
раз,
называется характеристическим временем
релаксации.
В равновесном положении система может находиться сколь угодно долго. Оно может быть изображено точкой на координатной плоскости, образованной какими-либо двумя параметрами состояния. Неравновесное состояние не может быть изображено точкой, т.к., хотя бы один параметр системы не будет иметь определенное значение для всего его объема.
При переходе из одного т. состояния системы в другое равновесие нарушается, значит, система проходит через последовательность неравновесных состояний. Нарушение равновесия тем сильней, чем быстрее проходит процесс перехода. Следовательно, при очень медленном переходе состояние системы в каждый момент является квазиравновесным. Значит, бесконечно медленный процесс перехода будет состоять из последовательности равновесных состояний. Такой процесс называется равновесным или квазистатическим.
Равновесный т. процесс может быть проведен в обратном направлении, при этом система будет проходить через те же состояния, что и при прямом переходе, но в обратной последовательности. Поэтому, равновесные процессы называют также обратимыми. Они могут быть изображены на координатной плоскости линией.
Процесс, при котором т. система после ряда изменений возвращается в исходное состояние, называется круговым процессом или циклом. Его графиком является замкнутая линия.
Все количественные выводы термодинамики применимы только к равновесным состояниям и обратимым процессам.
Б-2
-
Вектор перемещения, элементарное перемещение и путь, средняя и мгновенная скорость.
-
Уравнение динамики вращения твердого тела.
3. Температура. Шкала Цельсия, термодинамическая температурная шкала.
1. Перемещение, элементарное перемещение.
Вектором
перемещения
точки за промежуток от
 до
до
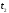 называется приращение радиус-вектора
называется приращение радиус-вектора
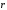 этой точки за этот промежуток
этой точки за этот промежуток
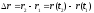 он направлен вдоль хорды стягивающий
соответствующий участок траектории
точки. Поэтому во всех случаях, кроме
премера, модуль перемещения меньше
длины пути за этот же
он направлен вдоль хорды стягивающий
соответствующий участок траектории
точки. Поэтому во всех случаях, кроме
премера, модуль перемещения меньше
длины пути за этот же
 .
На рисунке вектор перемещения
.
На рисунке вектор перемещения
 .
.
Однако,
по мере уменьшения длины пути разность
между хордой и перемещением уменьшается.
Следовательно, рассматривая элементарное
перемещение
 по траектории за достаточно малый
промежуток вреени
по траектории за достаточно малый
промежуток вреени
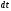 (от
(от
 до
до
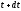 )
можно пренебречь отличием между
)
можно пренебречь отличием между
 и
и
 .
Значит, вектор
.
Значит, вектор
 направлени по касательной к траектории
в сторону движения точки. Также ка
единичный вектор касат.
направлени по касательной к траектории
в сторону движения точки. Также ка
единичный вектор касат.
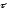 т.о.
т.о.
 вектор перемещения материальной точки
за любой
конечный промежуток времени от
вектор перемещения материальной точки
за любой
конечный промежуток времени от
 до
до
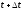 можно представить в виде:
можно представить в виде:
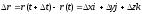
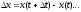 приращение
координат за
приращение
координат за
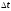 .
.
P.S.:
В математике
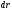 и
и
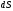 -
дифференциалы соответствующих функций
времени ??? т.е. линейные части приращений
этих функций при произвольном изменении
аргумента от
-
дифференциалы соответствующих функций
времени ??? т.е. линейные части приращений
этих функций при произвольном изменении
аргумента от
 до
до
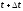 .
По определению в мтематике
.
По определению в мтематике

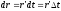 ,
,
а
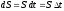 ;
;

 и
и
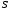 - производные т.е. приращение функций
- производные т.е. приращение функций
 и
и
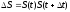 существует отличие от дифференциалов
этих функций. В физике различают
произвольное (конечное) приращение
аргумента
существует отличие от дифференциалов
этих функций. В физике различают
произвольное (конечное) приращение
аргумента
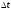 и дифференциала аргумента
и дифференциала аргумента
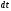 .
Под дифференциалом аргумента
.
Под дифференциалом аргумента
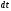 понимают столь малое его приращение
(элементарное), при котором разностью
между соответствующим приращением
функции
понимают столь малое его приращение
(элементарное), при котором разностью
между соответствующим приращением
функции
 и линейной частью её приращения
и линейной частью её приращения
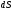 можно пренебречь т.е. ???
можно пренебречь т.е. ???
 .
Поэтому, в физике используют предложенные
Лейбницем обозначение производной
.
Поэтому, в физике используют предложенные
Лейбницем обозначение производной
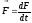
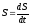 и трактуют эти выражения как отношения
не математической дифференциала функции
и аргумента, а малых (элеиентарных)
приращений функцмм м аргумента.
и трактуют эти выражения как отношения
не математической дифференциала функции
и аргумента, а малых (элеиентарных)
приращений функцмм м аргумента.
Скорость.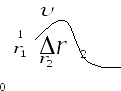
Для характеристики направления и быстроты движения точки вводится векторная физическая величина-скорость.
Пусть
за
 точка переместилась из т.1 в т.2. Вектор
перемещения
точка переместилась из т.1 в т.2. Вектор
перемещения
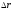 представляет собой приращение
радиус-вектора
представляет собой приращение
радиус-вектора
 за время
за время

 .
Отношение
.
Отношение
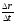 называется средней скоросью точки
называется средней скоросью точки
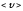 за время
за время
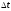 .
Направление
.
Направление
 совпадает с
совпадает с
 .
Скорость
.
Скорость
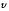 точки в заданный момент мремени
определяется как предел отношения
точки в заданный момент мремени
определяется как предел отношения
 при
при
 т.е.
т.е.
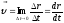
т.е.
производной от радиус-вектора
 по времени и направлению по касательной
к траектории в заданной точке в сторону
движения. Модуль
по времени и направлению по касательной
к траектории в заданной точке в сторону
движения. Модуль
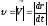 .
Вектор
.
Вектор
 можно разложить по базису
можно разложить по базису
 т.е. на три состояния по осям декартовой
системы координат
т.е. на три состояния по осям декартовой
системы координат
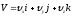 ;
;
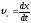 ;
;
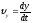 ;
;
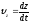 ;
;
 ;
;
2. Уравнение динамики вращения твердого тела.
Уравнение динамики твердого тела можно получить. Записав для производной момента импульса
 (уравнение
моментов)
(уравнение
моментов)
и
подставив значение
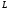 для твердого тела, вращающегося вокруг
произвольной оси
для твердого тела, вращающегося вокруг
произвольной оси
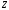 ;
;
 ;
;
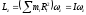


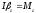 (*)
(*)
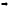
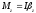 ;
;
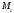 —суммарный
момент всех внешних сил относительно
оси вращения
—суммарный
момент всех внешних сил относительно
оси вращения
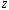 .
Отсюда видно, что (сравнивая с II-ым
законом Ньютона) во вращательном движении
тела роль массы играет
.
Отсюда видно, что (сравнивая с II-ым
законом Ньютона) во вращательном движении
тела роль массы играет
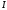 ,
а роль линейного ускорения
,
а роль линейного ускорения
 играет угловое ускорение
играет угловое ускорение
 ,
а роль результирующей силы —суммарный
момент внешних сил
,
а роль результирующей силы —суммарный
момент внешних сил
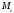 .
.
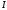 определяет инерциальные свойства. Если
масса не зависит от выбора С.О. то
определяет инерциальные свойства. Если
масса не зависит от выбора С.О. то
 зависит от оси. Относительно которой
определяется.
зависит от оси. Относительно которой
определяется.
Интегрирование
уравнения (*) с учетом начальных условий
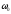 и
и
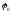 при
при
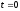 позволяет полностью решить задачу о
вращении твердого тела, т.е. найти
позволяет полностью решить задачу о
вращении твердого тела, т.е. найти
 ,
,
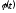 в любой момент времени в системе отсчета,
жестко связанной с осью вращения.
в любой момент времени в системе отсчета,
жестко связанной с осью вращения.
3. Температура
Температура системы, находящейся в равновесном состоянии, является мерой интенсивности теплового движения молекул, образующих систему. В этом состоит молекулярно-кинетическое истолкование температуры.
Если соприкасающиеся тела находятся в состоянии теплового равновесия, т.е., не обмениваются энергией путем теплопередачи, то им приписывают одинаковую температуру, а если при тепловом контакте одно из них передает энергию другому посредством теплопередачи, то первому приписывают большую температуру, второму – меньшую.
Средняя кинетическая энергия теплового движения частиц прямо- пропорциональна термодинамической температуре системы.
Для измерения температуры используется зависимость от температуры ряда физических свойств тела, называемого термометрическим, при прямом или косвенном измерении: длина, объем, сопротивление и др. Их изменение является основой для измерения температуры.
Для
практического измерения температуры
применяются температурные шкалы,
установленные с помощью термометрических
тел. В Международной стоградусной шкале
в качестве термометрического тела
берется вода и температура выражается
в градусах Цельсия. В термодинамической
температурной шкале температура
выражается в К и называется термодинамической
температурой. Связь между шкалами
 .
.
 К
называется абсолютный нуль температуры
или нуль по термодинамической шкале.
К
называется абсолютный нуль температуры
или нуль по термодинамической шкале.
Б-3
-
Ускорение, тангенциальное и нормальное ускорение.
-
Принцип работы гироскопа.
-
Уравнение состояния идеального газа. Уравнение Менделеева-Клапейрона.
1. Ускорение.
Движение точки характеризуется также ускорением—быстротой изменения скорости
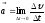 ;
;
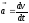
т.е.
вектор
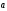 равен производной
равен производной
 по времени. Направление вектора
по времени. Направление вектора
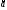 совпадает с направлением приращения
скорости
совпадает с направлением приращения
скорости
 за
за
 т.к.
т.к.
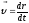 ,
то ускорение точки равно второй
производной по времени от радиус-вектора:
,
то ускорение точки равно второй
производной по времени от радиус-вектора:
 ;
;
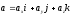 ;
;
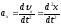 ;
;
где
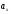 —проекция.
—проекция.
Если
траектории точки плоская кривая, то
можно выбрать два перпендикулярных
направления: касательная к траектории
(орт
 )
и нормали к ней
)
и нормали к ней
 .
Тогда
.
Тогда
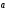 раскладывается по составляющим
раскладывается по составляющим
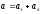 .
.
Т.к. вектор скорости направлен по касательной к траектории в сторону её движения, то
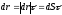 ;
;
 ;
;
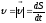 ;
;
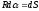
тогда
 ;
;
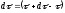 —приращение
орта касательной к траектории,
соответствующее элементарному пути
—приращение
орта касательной к траектории,
соответствующее элементарному пути
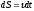 за
за
 .
.
Ввиду
малости
 его можно считать совпадающим с дугой
окружности радиуса
его можно считать совпадающим с дугой
окружности радиуса
 с центром в т.0 с центральным углом
с центром в т.0 с центральным углом
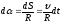 .
.
3. Уравнение состояния идеального газа
Состояние
данной массы газа определяется значением
трех параметров
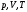 ,
изменение одного из них приводит к
изменению других. Соотношение, связывающее
эти параметры, представляет собой
уравнение состояния данной массы газа.
,
изменение одного из них приводит к
изменению других. Соотношение, связывающее
эти параметры, представляет собой
уравнение состояния данной массы газа.
Простейшим объектом, для которого рассмотрено уравнение состояния, является идеальный газ. Это газ, взаимодействием между молекулами которого можно пренебречь. Всякий реальный газ при достаточном разрежении близок к идеальному при комнатной температуре, особенно гелий и водород.
Экспериментально показано, что при небольших плотностях газы с хорошей точностью подчиняются уравнению:
 (1) -
уравнение состояния идеального газа.
(1) -
уравнение состояния идеального газа.
Согласно
закону Авогадро 1 моль любого газа
занимает при одинаковых условиях ( и
и
 )
одинаковый объем. В частности, при
нормальных :
)
одинаковый объем. В частности, при
нормальных :
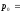 1
атм. и
1
атм. и
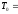 273К
объем одного моля газа
273К
объем одного моля газа
 равен
22,4 л. Значит, в формуле (1) для 1 моля любого
газа величина константы будет одной и
той же. Она обозначается как
равен
22,4 л. Значит, в формуле (1) для 1 моля любого
газа величина константы будет одной и
той же. Она обозначается как
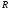 -
универсальная газовая постоянная,
-
универсальная газовая постоянная,
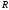
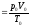 =
8,31Дж/моль К. Тогда уравнение состояния
1 моля газа:
=
8,31Дж/моль К. Тогда уравнение состояния
1 моля газа:
 (2).
(2).
Теперь
можно записать уравнение для произвольной
массы газа, учитывая, что при одинаковых
 и
и
 число молей
число молей
 газа будет занимать объем в
газа будет занимать объем в
 раз
больше:
раз
больше:
 ,
тогда умножив (2) на
,
тогда умножив (2) на
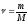 ,
получим:
,
получим:
 (3) – уравнение состояния для произвольной
массы газа. Оно называется также
уравнением Менделеева – Клапейрона.
(3) – уравнение состояния для произвольной
массы газа. Оно называется также
уравнением Менделеева – Клапейрона.
Если его правую часть умножить и разделить на число Авогадро, то получим:
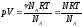 .
Или учитывая, что
.
Или учитывая, что
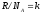 -
постоянная Больцмана, а
-
постоянная Больцмана, а
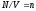 -
концентрация, получим окончательно:
-
концентрация, получим окончательно:
 -еще
одна форма уравнения состояния идеального
газа.
-еще
одна форма уравнения состояния идеального
газа.
Соответственно,
единичный вектор
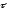 повор. на
повор. на
 .
Из равнобедренного треугольника
.
Из равнобедренного треугольника
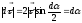 ,
ввиду малости
,
ввиду малости
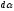 ;
по направлению
;
по направлению
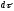 совпадает с
совпадает с
 (при
(при
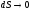
 )
)
0

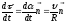 ;
;
и ускорение точки
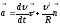 ;
;
 —
касательное(тангенциальное)
ускорение характеризует быстроту
изменения модуля скорости. При ускоренном
движении
—
касательное(тангенциальное)
ускорение характеризует быстроту
изменения модуля скорости. При ускоренном
движении
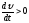 и
и
 совпадает с
совпадает с
 ,
при замедленном
,
при замедленном
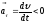 и
и
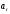 не совпадает с
не совпадает с
 .
.
Нормальное
ускорение
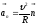 характеризует быстроту изменения
направления вектора скорости. Направлено
к центру кривизны траектории;
характеризует быстроту изменения
направления вектора скорости. Направлено
к центру кривизны траектории;
 ;
поэтому его называют центростремительным.
При прямолинейном движении
;
поэтому его называют центростремительным.
При прямолинейном движении
 .
.
Модуль
ускорения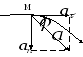
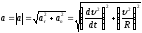 ;
;
При
ускоренном движении
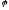 —
острый, при замедленном—тупой (
—
острый, при замедленном—тупой ( угол между
угол между
 и
и
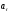 ).
Если
движение по окружности равномерное
).
Если
движение по окружности равномерное
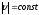 то
то
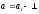 касательной.
касательной.
Б-4
-
Уравнение поступательного движения твердого тела.
-
Неинерциальные системы отсчета. Силы инерции.
3. Внутренняя энергия термодинамической системы. Внутренняя энергия идеального газа.
1. Динамика поступательного движения
2.1.
Простейшим видом механического движения
твердого тела является поступательное
движение. при котором прямая, соединяющая
любые две точки тела перемещается вместе
с телом, оставаясь || своему первоначальному
направлению (шарик на пружине относительно
Земли, поршень в цилиндре стационарного
двигателя, лифт, резец токарного станка
и др.). Траектории всех точек ела известны.
Радиус-вектор все точек тела за время
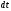 изменяется на одну и туже величину
изменяется на одну и туже величину
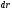 ,
скорости всех точек и ускорения одинаковы:
,
скорости всех точек и ускорения одинаковы:
 ;
;
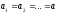
т.е. для
описания можно взять одну точку, если
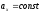 то
то

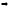
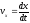
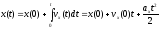
3.Внутренняя энергия системы
Полная
энергия т. системы равна сумме кинетической
энергии механического движения системы
как целого, потенциальной энергии
системы во внешнем поле ( гравитационном
или электромагнитном) и внутренней
энергии
 ,
зависящей только от внутреннего
состояния системы. Для неподвижных
систем, не подверженных действию внешних
сил, значение полной и внутренней энергий
совпадают.
,
зависящей только от внутреннего
состояния системы. Для неподвижных
систем, не подверженных действию внешних
сил, значение полной и внутренней энергий
совпадают.
Внутренняя энергия включает в себя энергии всевозможных видов движения и взаимодействия всех частиц (молекул, атомов, ионов и др.) системы, Например, для газа внутренняя энергия состоит из:
а) кинетической энергии теплового поступательного и вращательного движения молекул, а также колебательного движения атомов в молекулах;
б) потенциальной энергии, обусловленной силами межолекулярного взаимодействия;
в) энергии электронных оболочек атомов и ионов;
г) энергии движения и взаимодействия нуклонов в ядрах.
Внутренняя
энергия является однозначной функцией
состояния т.системы, Ее значение в каком
–либо произвольном состоянии системы
не зависит от того, каким образом пришла
система в это состояние. Т.е., изменение
внутренней энергии
 при переходе системы из состояния 1 в
состояние 2 не зависит от вида процесса
перехода и равно
при переходе системы из состояния 1 в
состояние 2 не зависит от вида процесса
перехода и равно
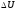
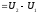 .
В частности, если система возвращается
в результате какого-либо перехода в
исходное состояние, то полное изменение
внутренней энергии равно нулю.
.
В частности, если система возвращается
в результате какого-либо перехода в
исходное состояние, то полное изменение
внутренней энергии равно нулю.
Подобно
потенциальной энергии в механике,
 определяется
с точностью до постоянной величины
определяется
с точностью до постоянной величины
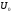 ,
зависящей от выбора отсчета внутренней
энергии, т.е., от выбора нуля. Так, как во
всех расчетах термодинамики находят
не абсолютное значение внутренней
энергии, а ее изменение
,
зависящей от выбора отсчета внутренней
энергии, т.е., от выбора нуля. Так, как во
всех расчетах термодинамики находят
не абсолютное значение внутренней
энергии, а ее изменение
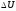 ,
то выбор
,
то выбор
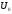 не играет роли.
не играет роли.
Составляющие внутренней энергии в) и г) не изменяются во всех процессах, не связанных с химическими реакциями и другими превращениями электронных оболочек атомов и ионов, а также ядерными реакциями и их можно не включать во внутреннюю энергию. Поэтому в дальнейшем под внутренней энергией в термодинамике будем понимать только сумму кинетической энергии теплового механического движения молекул и потенциальной энергии их взаимодействия. В идеальном газе последнее слагаемое равно нулю, значит его внутренняя энергия равна сумме кинетических энергий беспорядочного движения всех молекул.
Б-5
-
Закон инерции. Инерциальные системы отсчета.
-
Малые колебания. Диф. уравнение незатухающих колебаний и его решение.
3. Работа и теплота как два способа обмена энергией между термодинамической системой и внешними телами.
1. Закон инерции.
В основе классической механики лежит три закона Ньютона, сформулированные в сочинении «???», опубликованном в 1687г. Эти законы явились результатом гениального обобщения опытных данных и теоретических закономерностей в области механики, которые были установлены Ньютоном, а также Кеплером. Галилеем, Гюйгенсом. Гуком и др.
В качестве 1 закона динамики Ньютон принял закон, установленный еще Галилеем: Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит изменить это состояние.
Этот закон утверждает, что для состояния покоя или равномерно-прямолинейного движения не требуется внешних воздействий. В этом проявляется особое динамическое свойство тел, называемое инертностью. Поэтому 1 закон Ньютона называют законом инерции, а движение тела в отсутствии внешних воздействий, движение по инерции.
В этом законе считается, что тело не деформируется, т.е. оно абсолютно твердое, и что оно движется поступательно. Однако, твердое тело может еще вращаться по инерции. Необходимость во всех этих оговорках отпадает, если в законе Ньютона говорить не о теле, а о материальной точке, которая по определению не может ни деформироваться, ни вращаться.
Поэтому лучше пользоваться формулировкой:
материальная точка сохраняет состояние покоя или равномерно-прямолинейного движения до тех пор пока внешнее воздействие не выведет её из этого состояния.
Инерциальная система отсчета.
Известно что механическое движение относительно и его характер зависит от выбора системы отсчета. Первый закон выполняется не во всех системах отсчета. Например, тела, лежащие на гладком полу поезда, который идет равномерно и прямолинейно, могут прийти в движение относительно поезда по полу без всякого воздействия на них со стороны других тел. Для этого достаточно, чтобы поезд начал менять скорость хода, т.е. начал двигаться с ускорением.
Системы отсчета, по отношению к которым выполняется закон инерции, называются инерциальными системами отсчета.
Если бы такие системы нельзя было указать, то I-ый закон потерял бы смысл. Следовательно в I-ом законе имеется два утверждения: во-первых всем телам присуще свойство инертности, во-вторых можно указать системы отсчета, являющиеся инерционными.
Инерционной системой отсчета называют систему, в которой свободная от внешних воздействий материальная точка имеет равное нулю ускорение относительно нее, т.е. движется по инерции. Поэтому любые две инерционные системы отсчета либо неподвижны ??? либо движутся равномерно и прямолинейно.
Из опытов
известно, что с большой степенью точности
можно назвать инерционным гелиоцентр
системы отсчета. Начало координат – в
центре масс (практически в центре
Солнца), а оси взаимно
 и направлены ????. Земная система отсчета
неинерциальная из-за суточного вращения
Земли, однако это вращение медленное,
поэтому в большинстве практических
задач, эффекты связанные с вращением
Земли являются малыми и их можно не
учитывать, И Землю также можно считать
инерциальной системой отсчета.
и направлены ????. Земная система отсчета
неинерциальная из-за суточного вращения
Земли, однако это вращение медленное,
поэтому в большинстве практических
задач, эффекты связанные с вращением
Земли являются малыми и их можно не
учитывать, И Землю также можно считать
инерциальной системой отсчета.
Существует бесчисленное множество инерционных систем отсчета движущихся относительно друг друга прямолинейно и равномерно. Системы отсчета которые движутся с ускорением называются неинерциальными.
3. Работа и теплота
Обмен энергией между т.системой и внешними телами может происходить двумя качественно различными способами: путем совершения работы и путем теплопередачи. Первый способ, как известно из механики, осуществляется при силовом взаимодействии между телами. Энергия, передаваемая при этом т. системе внешними телами, называется работой, совершаемой над системой
Энергия, передаваемая внешними телами путем теплообмена, называется теплотой, получаемой т. системой от внешней среды.
Для совершения работы над неподвижной системой необходимо, чтобы перемещались внешние тела, т.е., чтобы изменялись внешние параметры состояния системы.
В
отсутствии внешних силовых полей обмен
энергией между неподвижной системой и
внешней средой путем совершения работы
происходит только при изменении объема
и формы системы. Например, работу над
газом производят силы давления на газ
со стороны внешней среды. При этом работа
внешних сил над системой
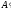 ,
численно равна и противоположна по
знаку работе
,
численно равна и противоположна по
знаку работе
 ,
совершаемой самой системой над внешней
средой, т.е., против внешних сил.
,
совершаемой самой системой над внешней
средой, т.е., против внешних сил.
В отличие от внутренней энергии системы, являющейся однозначной функцией состояния этой системы, понятие теплоты и работы имеют смысл только в связи с видом процесса изменения состояния системы. Они являются энергетическими характеристиками конкретного процесса.
Существует
качественное различие между совершением
работы и теплообменом, как способами
обмена энергией между макросистемами.
Совершение работы над системой может
изменить любой вид энергии системы.
Например, при неупругом соударении тел
часть совершенной работы идет на
изменение кинетической энергии, а часть
работы – на приращение внутренней
энергии. Если же энергия сообщается в
виде теплоты, то она идет только на
увеличение энергии теплового движения
молекул, т.е. на
 .
.
Б-6
-
Сила. Масса тела.
-
Центробежная сила инерции.
3. Первый закон термодинамики.
1. Сила. Ньютоновское определение.
Сила — мера механического воздействия одного тела на другое, векторная величина. Взаимодействие может осуществляться непосредственно в контакте или между удаленными телами, с помощью физических полей: гравитационное, электромагнитное. Сила задана, если указаны её модуль, направление и точка приложения.
Из опытов
следует что действие нескольких сил на
тело которые приложены в одной точке
можно заменить действием одной силы,
равной их геометрической сумме
 .
Приложенной в той же точке называется
результирующей. В основ механического
явления лежат гравитационное и
электромагнитное взаимодействия.
Однако,
для практических задач вводят следующие
силы:
.
Приложенной в той же точке называется
результирующей. В основ механического
явления лежат гравитационное и
электромагнитное взаимодействия.
Однако,
для практических задач вводят следующие
силы:
-
Сила тяжести
 ;
; -
Упругости сила
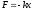 ;
; -
Сила трения
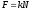 ;
; -
Сила сопротивления среды
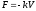 ;
;
2.5. Масса. 2-ой закон Ньютона.
Основная
задача механики заключается в определении
характеристик движения тел под действием
приложенных к ним сил. Из опыта известно,
что под действием силы
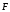 свободное твердое тело изменяет свою
скорость, приобретая ускорение
свободное твердое тело изменяет свою
скорость, приобретая ускорение
 ,
это ускорение пропорционально силе и
совпадает с ней по направлению.
,
это ускорение пропорционально силе и
совпадает с ней по направлению.
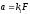 (*)
(*)
где
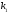 —
коэффициент пропорциональности;
—
коэффициент пропорциональности;
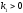 ,
постоянный для каждого конкретного
тела, разный для разных тел. Это
соотношение(*) отражает свойство
инертности тел, согласно которому тела
изменяют скорость не мгновенно, а
постепенно, приобретая под действие
,
постоянный для каждого конкретного
тела, разный для разных тел. Это
соотношение(*) отражает свойство
инертности тел, согласно которому тела
изменяют скорость не мгновенно, а
постепенно, приобретая под действие
 конечное
ускорение.
конечное
ускорение.
В качестве
меры инертности в механике вводится
положительная величина
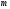 —масса
тела. Чем больше инертность, а следовательно,
его масса, тем меньше
—масса
тела. Чем больше инертность, а следовательно,
его масса, тем меньше
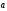 оно должно приобретаться под действием
одной и той же силы. Поэтому приняв в
(*)
оно должно приобретаться под действием
одной и той же силы. Поэтому приняв в
(*)
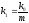 ;
;
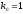 во всех системах ??? получим:
во всех системах ??? получим:
 —
второй
закон Ньютона;
—
второй
закон Ньютона;
Отсюда
следует, что
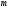 величина постоянная для данного тела
(по Ньютону масса количество материи),
не зависящая от состояния движения
тела. Ни от его положения в пространстве,
ни от действия других тел. Поэтому для
сравнения масс двух тел достаточно
сравнить ускорения
величина постоянная для данного тела
(по Ньютону масса количество материи),
не зависящая от состояния движения
тела. Ни от его положения в пространстве,
ни от действия других тел. Поэтому для
сравнения масс двух тел достаточно
сравнить ускорения
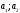 ,
приобретенные ими под действием
одинаковой силы;
,
приобретенные ими под действием
одинаковой силы;
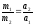 ;
;
Из опыта следует, что масса величина аддитивная, т.е. масса тела равна сумме масс всех составляющих его частей. Масса произвольной механической системы равна сумме масс материальных точек, на которые эту систему можно разбить.
Обычно
массу тела определяют сравнением её с
массой эталонных тел (гирь) путем
взвешивания на рычажных весах. Этот
метод основывается на том, что в одной
и той же точке земного шара все тела
падают с одним ускорением
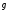 .
Свободное падение обусловлено действием
единственной силы—силы тяжести
.
Свободное падение обусловлено действием
единственной силы—силы тяжести
 ,
так что согласно (*):
,
так что согласно (*):
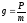 ;
;
и отношение масс:
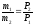 ;
;
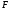
Инертность можно продемонстрировать: скатерть из-под накрытого стола, вертикальный шарик на нити тянуть за нитку.
3. Первый закон термодинамики
Равновесный
процесс перехода т. системы из начального
состояния 1 в другое – 2 можно рассмотреть
с точки зрения закона сохранения энергии.
Изменение внутренней энергии системы
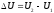 в таком процессе равно сумме работы,
совершенной внешними силами над системой
в таком процессе равно сумме работы,
совершенной внешними силами над системой
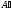 и теплоты, сообщенной системе,
и теплоты, сообщенной системе,
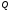 :
:
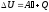 .
.
Работа
 численно
равна и противоположна по знаку работе
численно
равна и противоположна по знаку работе
 ,
совершаемой самой системой против
внешних сил в том же равновесном переходе:
,
совершаемой самой системой против
внешних сил в том же равновесном переходе:
 ,
тогда первый закон термодинамики можно
записать в виде:
,
тогда первый закон термодинамики можно
записать в виде:
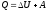 ,
,
т.е., теплота, сообщенная системе, идет на приращение внутренней энергии и на совершение системой работы над внешними телами.
Обычно
первый закон записывают для изменения
состояния системы при сообщении ей
малого количества теплоты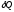 ,
совершением системой малой (элементарной)
работы
,
совершением системой малой (элементарной)
работы
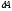 и элементарному изменению (приращению)
внутренней энергии
и элементарному изменению (приращению)
внутренней энергии
 :
:

Отличие
в записи малых величин теплоты и работы
и изменении внутренней энергии не
формальны, а отражают глубокое физическое
различие этих величин. Дело в том, что
внутренняя энергия системы является
однозначной функцией ее состояния. Ее
значение в каком-либо произвольном
состоянии не зависит от того, каким
способом система пришла в это состояние,
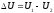 .
При совершении системой процесса, в
результате которого она вновь возвращается
в исходное состояние, полное изменение
энергии
.
При совершении системой процесса, в
результате которого она вновь возвращается
в исходное состояние, полное изменение
энергии
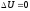 ,
т.е., интеграл:
,
т.е., интеграл:
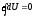
Это
тождество является необходимым и
достаточным условием для того, чтобы
выражение
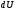 представляло
собой полный дифференциал. Ни работа,
ни теплота не являются функциями
состояния и поэтому
представляло
собой полный дифференциал. Ни работа,
ни теплота не являются функциями
состояния и поэтому
 и
и
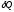 не являются полными дифференциалами.
По определению из математики полный
дифференциал функции:
не являются полными дифференциалами.
По определению из математики полный
дифференциал функции:
 ,
т.е., определяется значениями функции
в конечном и начальном состояниях и не
зависит от пути перехода.
,
т.е., определяется значениями функции
в конечном и начальном состояниях и не
зависит от пути перехода.
Все
физические величины, входящие в 1 закон
термодинамики могут быть больше нуля
или меньше нуля, возможно также, что
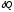 =
0 и
=
0 и
 = 0. Если теплота подводится,
= 0. Если теплота подводится,
 0,
если отводится, то
0,
если отводится, то
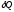
0. На одних участках перехода она может
быть положительна, на других –
отрицательна.
0. На одних участках перехода она может
быть положительна, на других –
отрицательна.
Общее
количество теплоты, сообщенное системе
в конечном процессе перехода 1 – 2 равно
алгебраической сумме теплот
 ,
сообщенных на всех участках процесса:
,
сообщенных на всех участках процесса:
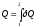 .
.
Работа,
совершаемая системой в конечном процессе
1 – 2 равна алгебраической сумме работ
 ,
т.е.,
,
т.е.,
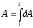
Изменение внутренней энергии в этом конечном переходе:
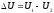 и
не зависит от вида перехода.
и
не зависит от вида перехода.
Б-7
-
Основное уравнение динамики материальной точки. Элементарный импульс силы и импульс силы.
-
Сила Кориолиса.
-
Работа идеального газа при расширении.
1. Основной закон динамики материальной точки.
Уравнение
 описывает изменение движения протяженного
тела под действием силы при отсутствии
деформации и оно движется. Для точки
оно справедливо всегда. поэтому его
можно рассматривать как основной закон
движения материальной точки: ускорение
материальной точки пропорционально
вызывающей его силе, совпадает с ней по
направлению и обратно пропорционально
массе материальной точки. В механике
Ньютона масса не зависит от характеристик
движения,
описывает изменение движения протяженного
тела под действием силы при отсутствии
деформации и оно движется. Для точки
оно справедливо всегда. поэтому его
можно рассматривать как основной закон
движения материальной точки: ускорение
материальной точки пропорционально
вызывающей его силе, совпадает с ней по
направлению и обратно пропорционально
массе материальной точки. В механике
Ньютона масса не зависит от характеристик
движения,
 ,
,
 ускорение
ускорение
 ;
;
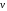 —скорость
точки, тогда
—скорость
точки, тогда
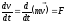 или
или
 (**).
(**).
Вектор
 называют импульсом материальной точки.
В теоретической механике(а раньше и в
физике) вектор
называют импульсом материальной точки.
В теоретической механике(а раньше и в
физике) вектор
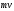 называют количеством движения. Импульс
одна из важнейших динамических
характеристик материальной точки
называют количеством движения. Импульс
одна из важнейших динамических
характеристик материальной точки
В форме (**) основной закон динамики материальной точки утверждает, что скорость изменения импульса материальной точки равна действующей на нее силе. В этом состоит (согласно современной терминологии) второй закон Ньютона.
Основной
закон динамики материальной точки
выражает принцип причин в классической
механике, т.к. устанавливает однозначную
связь между изменением со временем
состояния движения и положения
материальной точки в пространстве и
действия на нее силы. Закон позволяет
по начальному состоянию точки (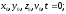 )
и действующей силы рассчитать состояние
материальной точки в любой последующий
момент времени.
)
и действующей силы рассчитать состояние
материальной точки в любой последующий
момент времени.
На основании обобщения опытных фактов был установлен важный принцип независимости действия сил: если на материальную точку одновременно действует несколько сил, то каждая из них, сообщает материальной точке такое же ускорение, как если бы других сил не было. Т.о.
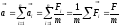 ;
;
 —результирующая
сила;
—результирующая
сила;
Основной закон можно переписать в виде:
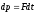 ;
;
вектор
 называется элементарным импульсом силы
за малый промежуток времени
называется элементарным импульсом силы
за малый промежуток времени
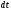 её действия. Т.о. из основного закона и
принципа независимости действия сил
следует, что изменение импульса
материальной точки за малый промежуток
времени
её действия. Т.о. из основного закона и
принципа независимости действия сил
следует, что изменение импульса
материальной точки за малый промежуток
времени
 равно элементарному импульсу результирующих
всех сил, действующих на эту точку за
тот же
равно элементарному импульсу результирующих
всех сил, действующих на эту точку за
тот же
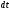 .
.
Изменение
импульса за конечный промежуток времени
от
 до
до

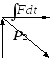
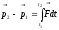 —импульс
силы;
—импульс
силы;

если
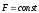 то
то
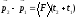 ,
,
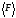 среднее значение силы за
среднее значение силы за
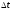 .
.
3. Работа при расширении или сжатии газа
Найдем
работу, которая совершается при расширении
или сжатии газа, заключенного в сосуде
с подвижным поршнем площадью
 .
Внешняя сила, действующая на поршень
.
Внешняя сила, действующая на поршень
 . При перемещении поршня вверх на малое
расстояние
. При перемещении поршня вверх на малое
расстояние
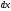 газ совершает элементарную работу
газ совершает элементарную работу
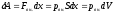 ,
где
,
где
 -
изменение объема газа. Если изменение
объема происходит квазистатически, то
в любой момент времени газ находится в
равновесном состоянии с внешней средой
и его давление
-
изменение объема газа. Если изменение
объема происходит квазистатически, то
в любой момент времени газ находится в
равновесном состоянии с внешней средой
и его давление
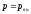 Элементарная работа газа в равновесном
(квазистатическом) процессе изменения
его объема:
Элементарная работа газа в равновесном
(квазистатическом) процессе изменения
его объема: .
Т.к.,
.
Т.к.,
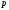
0, то при расширении газ совершает
положительную работу. При сжатии
0, то при расширении газ совершает
положительную работу. При сжатии
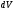
0, значит,
0, значит,
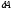
0 – работа газа отрицательна, положительную
работу в этом случае совершают внешние
силы.
0 – работа газа отрицательна, положительную
работу в этом случае совершают внешние
силы.
Если
давление постоянное, то работа
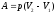 ,
при
,
при
 работа вычисляется как сумма элементарных
работ, т.е., путем интегрирования:
работа вычисляется как сумма элементарных
работ, т.е., путем интегрирования:
 .
Это численно равно площади под кривой
.
Это численно равно площади под кривой

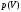 на
соответствующем графике, рис. Эти
выражения справедливы при любых
изменениях объема твердых, жидких и
газообразных тел.
на
соответствующем графике, рис. Эти
выражения справедливы при любых
изменениях объема твердых, жидких и
газообразных тел.
Б-8
-
Третий закон Ньютона.
-
Гармонические колебания. Уравнение гармонических колебаний.
Потенциальная и кинетическая энергия колебаний.
-
Изопроцессы идеального газа: изохорный.
1. наблюдения и опыты свидетельствуют, что механическое действие тел одного на другое всегда является взаимодействием. Если тело 2 действует на тело 1, то тело 1 обязательно действует на тело 2. на ведущие колеса автомобиля со стороны шоссе действует сила трения покоя в сторону движения автомобиля, а колеса действуют на шоссе с силами трения покоя в противоположные стороны.
Количественное
описание механического взаимодействия
было дано Ньютоном в его III-ем
законе динамики.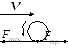
Действию всегда есть равное и противоположное противодействие, взаимодействия двух тел друг на друга равны между собой и направлены в противоположные стороны.
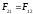
для точек: две материальные точки действуют друг на друга с силами равными по величине, направленные в противоположные стороны вдоль линий их соединения.
3.
Уравнение первого закона термодинамики
можно записать для равновесных процессов
изменения его состояния в ином виде,
используя выражения для теплоемкости
однородного тела, откуда
 или с учетом молярной теплоемкости:
или с учетом молярной теплоемкости:
 ,
а для одного моля
,
а для одного моля
 .
.
Тогда первый закон можно записать в виде:
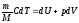
Применим его к различным изопроцессам идеального газа.
Изохорный
процесс,
 .(закон
Шарля).
.(закон
Шарля).
На
диаграмме
 это
вертикальная прямая: 1 – 2 нагрев , а 1 -
3 охлаждение. Практически этот процесс
проводят, изменяя температуру газа,
находящегося в толстостенном сосуде с
неизменным объемом. В этом процессе
работа не совершается:
это
вертикальная прямая: 1 – 2 нагрев , а 1 -
3 охлаждение. Практически этот процесс
проводят, изменяя температуру газа,
находящегося в толстостенном сосуде с
неизменным объемом. В этом процессе
работа не совершается:
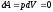 .
Вся теплота идет на изменение его
внутренней энергии.
.
Вся теплота идет на изменение его
внутренней энергии. ,
,
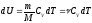 (1), где
(1), где
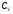 -
молярная теплоемкость при постоянном
объеме. Из опытов известно, что
-
молярная теплоемкость при постоянном
объеме. Из опытов известно, что
 зависит от химического состава газа и
его Т. Для не очень широкой области
температур можно считать, что
зависит от химического состава газа и
его Т. Для не очень широкой области
температур можно считать, что
 =const.
=const.
При изохорном конечном нагреве газа от температуры Т1 до температуры Т2 изменение внутренней энергии равно
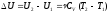 (2),
и теплота, сообщенная системе:
(2),
и теплота, сообщенная системе:
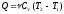 (3)
(3)
Для
идеального газа внутренняя энергия это
энергия теплового движения молекул,
непосредственно не зависящая от объема
(расстояния между молекулами), как в
реальных газах. При расширении и сжатии
газа его
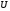 будет
изменяться только за счет изменения
кинетической энергии теплового движения,
т.е., за счет температуры. Таким образом,
соотношения (1) и (2) справедливы для
любого процесса изменения состояния
идеального газа, а не только изохорного.
Внутренняя энергия газа зависит только
от его массы, химического состава и
температуры. Это подтверждается опытами
Гей – Люссака и Джоуля.
будет
изменяться только за счет изменения
кинетической энергии теплового движения,
т.е., за счет температуры. Таким образом,
соотношения (1) и (2) справедливы для
любого процесса изменения состояния
идеального газа, а не только изохорного.
Внутренняя энергия газа зависит только
от его массы, химического состава и
температуры. Это подтверждается опытами
Гей – Люссака и Джоуля.
Значит, для любого равновесного процесса изменения состояния идеального газа уравнение первого закона термодинамики имеет вид:
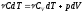 (4)
(4)
Б-9
1. Затухающие колебания. Период колебаний. Добротность.
2. Принцип относительности Галилея.
3. Изопроцессы идеального газа: изобарный.
2. Принцип относительности Галилея
Значит
ускорение какого-либо тела во всех
системах отсчета, движущихся друг
относительно друга прямолинейно и
равномерно одинаково. Тогда если одна
из систем инерциальная, то другая также
будет инерциальная
 .
.
А значит
и силы действующие на тела в разных
инерциальных системах одинаковы. Масса
в Ньютоновской механике также одинакова
во всех системах отсчета. Из сказанного
следует вывод, что уравнение динамики

 не изменяется при переходе от одной
инерциальной системы отсчета к другой
или как говорят они инвариантны по
отношению к преобразованию координат,
соответствующему переходу от одной
инерциальной системы отсчета к другой.
Это значит что, с механической точки
зрения все инерциальные системы отсчета
эквивалентны, ни одной из них нельзя
отдать предпочтение перед другими.
Практически ни какими опытами нельзя
установить находится ли данная ИСО в
покое или движется равномерно и
прямолинейно. Находясь, например, в
вагоне поезда, движущегося равномерно
и прямолинейно нельзя установить (не
выглянув в окно) движется ли он или
находится в состоянии покоя. Мяч в вагоне
поезда получит такое же ускорение, как
и на Земле при действии одинаковой силы.
Свободное падение тел и другие механические
процессы будут происходить в вагоне
также как если бы он покоился. подобное
наблюдение и опыты проводил еще Галилей,
поэтому положение о том, что все
механические явления в разных ИСО
протекают одинаковым образом это
называется принципом относительности
Галилея.
не изменяется при переходе от одной
инерциальной системы отсчета к другой
или как говорят они инвариантны по
отношению к преобразованию координат,
соответствующему переходу от одной
инерциальной системы отсчета к другой.
Это значит что, с механической точки
зрения все инерциальные системы отсчета
эквивалентны, ни одной из них нельзя
отдать предпочтение перед другими.
Практически ни какими опытами нельзя
установить находится ли данная ИСО в
покое или движется равномерно и
прямолинейно. Находясь, например, в
вагоне поезда, движущегося равномерно
и прямолинейно нельзя установить (не
выглянув в окно) движется ли он или
находится в состоянии покоя. Мяч в вагоне
поезда получит такое же ускорение, как
и на Земле при действии одинаковой силы.
Свободное падение тел и другие механические
процессы будут происходить в вагоне
также как если бы он покоился. подобное
наблюдение и опыты проводил еще Галилей,
поэтому положение о том, что все
механические явления в разных ИСО
протекают одинаковым образом это
называется принципом относительности
Галилея.
3.
Изобарный процесс,
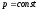 .
( Закон Гей -Люссака)
.
( Закон Гей -Люссака)
Он реализуется при нагревании газа в цилиндре с подвижным поршнем, на который действует постоянное внешнее давление.
На рис. изображены процессы изобарного расширения газа при его нагревании (1-2) и изобарного сжатия при его охлаждении (2-3).
Элементарная теплота, сообщенная газу в изобарном процессе:
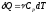 (5),
где
(5),
где
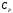 -
молярная теплоемкость при постоянном
давлении.
-
молярная теплоемкость при постоянном
давлении.
Элементарная работа, совершенная идеальным газом при этом:
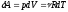 (6),
учитывая уравнение Менделеева
–Клапейрона.
(6),
учитывая уравнение Менделеева
–Клапейрона.
Из
последнего уравнения можно выяснить
смысл
 :
:
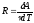 ,
т.е. универсальная газовая постоянная
численно равна работе, совершенной
одним молем идеального газа при его
изобарном нагревании на 1К.
,
т.е. универсальная газовая постоянная
численно равна работе, совершенной
одним молем идеального газа при его
изобарном нагревании на 1К.
Подставим
в первый закон выражения для
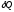 и
и
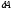 и найдем связь между
и найдем связь между
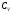 и
и
 :
:
 ,
откуда:
,
откуда:
 (7) – уравнение Майера для молярных
теплоемкостей. Отсюда видно, что при
изобарном нагревании газа к нему должна
быть подведена большая теплота, чем для
такого же изохорного нагревания, разность
их равна работе, совершенной газом при
изобарном расширении.
(7) – уравнение Майера для молярных
теплоемкостей. Отсюда видно, что при
изобарном нагревании газа к нему должна
быть подведена большая теплота, чем для
такого же изохорного нагревания, разность
их равна работе, совершенной газом при
изобарном расширении.
Работа газа при изобарном расширении при переходе из состояния 1 в состояние 2 , рис.
 (8).
(8).
Если
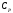 постоянная, то теплота, сообщенная газу
в изобарном процессе:
постоянная, то теплота, сообщенная газу
в изобарном процессе:
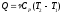 (9),
а изменение внутренней энергии в
процессе:
(9),
а изменение внутренней энергии в
процессе:
 (10).
(10).
Б-10
-
Преобразования Галилея.
-
Вынужденные колебания.
-
Изопроцессы идеального газа: изотермический.
3. Изотермический процесс, Т=const. (закон Бойля – Мариотта)
Может происходить в условиях, когда теплообмен между газом и внешней средой осуществляется при постоянной (конечной) разности температур. Для этого теплоемкость внешней среды должна быть велика и процесс расширения или сжатия должен идти весьма медленно (для квазиравновесия). Изотермическими являются процессы кипения, конденсации, плавления и кристаллизации химически чистых веществ, происходящих при постоянном давлении.
Для
идеального газа в этом процессе
выполняется закон Бойля – Мариотта:
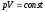 ,
графиком которого является гипербола,
рис. . Внутренняя энергия газа постоянна
в процессе, значит:
,
графиком которого является гипербола,
рис. . Внутренняя энергия газа постоянна
в процессе, значит:
 (11) , а
(11) , а
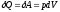 ,
,
т.е., вся теплота, сообщенная системе, идет на совершение газом работы против внешних сил:
 (12)
(12)
При
изотермическом расширении
 ,
к нему подводится теплота
,
к нему подводится теплота
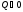 ,
газ совершает положительную работу,
,
газ совершает положительную работу,
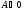 ,
рис. , процесс 1-2. При сжатии газа,
процесс 1-3, работа, совершенная газом
отрицательна, положительную работу при
этом выполняют внешние силы, От газа
отводится теплота
,
рис. , процесс 1-2. При сжатии газа,
процесс 1-3, работа, совершенная газом
отрицательна, положительную работу при
этом выполняют внешние силы, От газа
отводится теплота
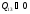 .
.
Теплоемкость
газа в изотермическом процессе

,
т.к.,
,
т.к.,
 .
.
Б-11
-
Закон сохранения импульса системы.
-
Резонанс.
-
Изопроцессы идеального газа: адиабатный.
1. . Закон сохранения импульса системы.
Импульсом
тела или материальной точки является
произведение,
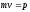 т.е. вектор. Если взять замкнуть или
изолировать систему тел или точек, то
импульс такой системы будет равен
геометрической сумме импульсов точек,
составляющих систему
т.е. вектор. Если взять замкнуть или
изолировать систему тел или точек, то
импульс такой системы будет равен
геометрической сумме импульсов точек,
составляющих систему
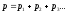 .
.
Импульс
является одной из важнейших физических
категорий (величин) по той причине, что
в замкнутой системе он (вектор
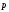 )
не изменяется, какие бы движения не
происходили внутри системы. Это положение
носит название закона
сохранения импульса.
)
не изменяется, какие бы движения не
происходили внутри системы. Это положение
носит название закона
сохранения импульса.
Закон сохранения импульса следует непосредственно из законов Ньютона. Для каждого из тел замкнутой системы можно записать основной закон
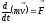 или
или
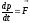 ;
;
Если
записать это уравнение для первого
тела, то в правой части будет стоять
сумма сил, действующих на него со стороны
остальных тел:
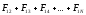 ;
для второго
;
для второго
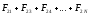 ;
;
И так
далее или в общей форме т.е. для
 тела
тела
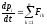 (
(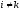 ),
),
а для всех тел
 (
(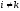 ).
).
По
третьему закону Ньютона силы взаимодействия
 и
и
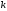 тел
равны по величине и противоположны по
направления
тел
равны по величине и противоположны по
направления
 так, что
так, что
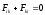 .
Эти силы являются внутренними в системе
и их сумма равна
.
Эти силы являются внутренними в системе
и их сумма равна
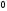 .
.
Левую часть по известному правилу дифференцирования суммы можно записать
 .
.
Т.о.
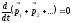 ;
т.е.
;
т.е.
 .
.
Т.е. величина и направление импульсов отдельных тел могут меняться, но их геометрическая сумма в замкнутой системе сохраняется. Если действуют внешние силы то
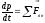 .
.
Т.е. можно сказать, что причина изменения импульса системы — действие внешних сил. Это справедливо. Разумеется, только по отношению к инерциальным системам отсчета.
Импульс может сохраняться и не у замкнутой системы, если результирующая внешних сил равна 0.
У
незамкнутой системы может сохраняться
не сам импульс
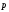 ,
а его проекция
,
а его проекция
 на некоторое направление
на некоторое направление
 .
Это бывает, если проекция результирующей
силы на это направление
.
Это бывает, если проекция результирующей
силы на это направление
 т.е.
т.е.
 .
Например, при движении системы в
однородном поле сил тяжести сохраняется
.
Например, при движении системы в
однородном поле сил тяжести сохраняется
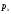 ,
что бы в системе не происходило.
,
что бы в системе не происходило.
Подчеркнем,
что закон сохранения импульса возможен
только в инерциальной системе. Это не
исключает случаев, когда
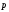 сохранялся бы и в неинерциальной системе
отсчета. Для этого достаточно в уравнении
сохранялся бы и в неинерциальной системе
отсчета. Для этого достаточно в уравнении
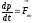 .
.
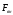 , которая включает и силы инерции была
равна 0. это может выполняться при
специальных условиях.
, которая включает и силы инерции была
равна 0. это может выполняться при
специальных условиях.
3.
Адиабатный процесс,
 .
.
Это процесс, при котором система не обменивается теплотой с окружающей средой. Практически процесс производят при достаточно быстром расширении или сжатии газа.
Тогда из первого закона следует:
 - система
совершает работу за счет убыли внутренней
энергии. Или, записывая более подробно,
получим:
- система
совершает работу за счет убыли внутренней
энергии. Или, записывая более подробно,
получим:
 (13)
(13)
Здесь
теплоемкость при адиабатном процессе
- ,
т.к.,
,
т.к.,
 .
.
Из (13)
видно, что
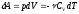 (14)
(14)
При
расширении
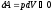 и
и
 ,
газ охлаждается, при адиабатном сжатии
,
газ охлаждается, при адиабатном сжатии
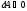 и
и
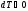 ,
газ нагревается.
,
газ нагревается.
Связь
между параметрами состояния адиабатного
процесса можно найти, взяв дифференциалы
от
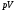 и от уравнения Менделеева - Клапейрона:
и от уравнения Менделеева - Клапейрона:
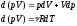 (15) , отсюда можно выразить
(15) , отсюда можно выразить
 , подставить в уравнение (14) и получить:
, подставить в уравнение (14) и получить:
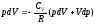 .
Заменив здесь
.
Заменив здесь
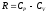 из уравнения Майера, получим после
простых преобразований:
из уравнения Майера, получим после
простых преобразований:
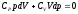 ,
далее разделим переменные, поделив
уравнение на
,
далее разделим переменные, поделив
уравнение на
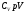 и обозначим
и обозначим
 -
показатель адиабаты или постоянная
Пуассона.
-
показатель адиабаты или постоянная
Пуассона.
Тогда 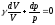 .
После интегрирования
.
После интегрирования
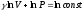 или:
или:

Это есть уравнение адиабаты или уравнение Пуассона. С помощью уравнения Менделеева – Клапейрона его можно записать через другие параметры:
 или
или
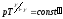 .
.
Из рис.
видно, что адиабата идет круче, чем
изотерма, поскольку
 для любого идеального газа. Это объясняется
тем, что при адиабатном сжатии увеличение
давления происходит не только из-за
уменьшения объема, как в изотермическом
процессе, но и из-за возрастания
температуры. При адиабатном расширении
газа его температура уменьшается и
давление падает сильнее, чем при
соответствующем изотермическом
расширении.
для любого идеального газа. Это объясняется
тем, что при адиабатном сжатии увеличение
давления происходит не только из-за
уменьшения объема, как в изотермическом
процессе, но и из-за возрастания
температуры. При адиабатном расширении
газа его температура уменьшается и
давление падает сильнее, чем при
соответствующем изотермическом
расширении.
Работа в адиабатном (конечном) процессе 1-2 ( на рис. площадь под кривой)
Б-12
-
Энергия и работа. Элементарная работа и работа.
-
Распространение волн в упругой среде. Волновой фронт. Волновая поверхность.
-
Характер теплового движения молекул.
