2. Построение эмпирической линии регрессии

Как указывалось в разделе 4.2 данная задача разбивается на 5 этапов. Рассмотрим реализацию каждого из них.

1. Нахождение минимального и максимального значений X

1) Перейти на лист с введенными табличными данными.

2) В ячейках под введенными табличными данными ввести текст max и min (см. рисунок).

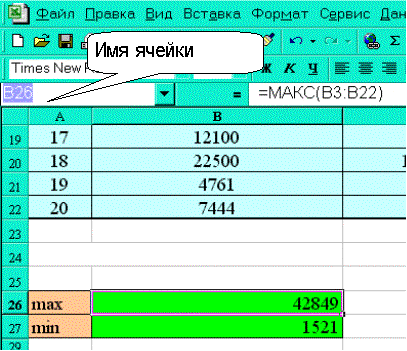
3) С использованием Мастера функций, функций МАКС и МИН в соответствующих ячейках вычислить максимальное и минимальное значение среди значений столбца Кол-во потребленных Ккал (X) (см. рисунок).

4) Переименовать ячейки, содержащие минимальное и максимальное значения, присвоив им соответственно имена max и min следующим образом:

• установить табличный курсор в ячейку, имя которой требуется изменить;

• щелкнуть левой клавишей «мыши» на имени ячейки (в поле «Имя») (см. рисунок);

• ввести новое имя;

• подтвердить ввод имени нажатием Enter (см. рисунок);

• проверить установку имени щелчками на ячейках В26 (в поле «Имя» появится «max») и В27 (в поле «Имя» появится «min»).

2. Разбиение отрезка экспериментальных значений на интервалы

Разбиение на интервалы заключается в нахождении начального и конечного значений каждого интервала. Эта процедура выполняется следующим образом:

1) Найти длину каждого интервала по формуле  длина интервала=(max- min)/5 

• ввести эту формулу в ячейку, расположенную под значениями max и min (см. рисунок);

• переименовать ячейку со значением длины каждого интервала, присвоив ей имя dx (см. рисунок).

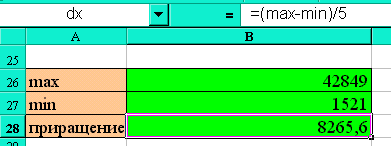
2) В ячейки, расположенные ниже вычисленного приращения, ввести текст x1, x2, x3, x4, x5, x6 (см. рисунок), исходя из следующих соображений:

1-й интервал – [x1, x2]

2-й интервал – [x2, x3]

3-й интервал – [x3, x4]

4-й интервал – [x4, x5]

5-й интервал – [x5, x6]

3) В строке, следующей за обозначениями границ интервалов, ввести формулы:

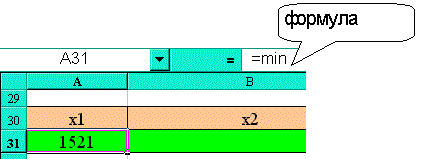
• в ячейку под x1 ввести =min (см. рисунок);

;

• в следующую справа ячейку ввести =А31+dx (см. рисунок);

• скопировать вправо последнюю введенную формулу; последнее значение должно находится под x6 (см. рисунок);

• переименовать ячейки с полученными значениями, присвоив им соответственно имена xx1, xx2, xx3, xx4, xx5, xx6 и проверить переименование.

4) В ячейки, расположенные ниже вычисленных границ интервалов, ввести обозначения средних точек интервалов x12, x23, x34, x45, x56 (см. рисунок), исходя из следующих соображений:

x12 – середина интервала [x1, x2]

x23 – середина интервала [x2, x3]

x34 – середина интервала [x3, x4]

x45 – середина интервала [x4, x5]

x56 – середина интервала [x5, x6]

5) В ячейки, расположенные ниже введенных обозначений, ввести формулы для вычисления середин интервалов:

• в ячейку под x12 ввести формулу вычисления среднего значения между x1 и x2 (см. рисунок);

• последовательно скопировать вправо в ячейки В34:Е34 введенную формулу; последнее значение должно находиться под x56 (см. рисунок).

3. Нахождение экспериментальных данных, попавших в каждый интервал

Идея нахождение точек , попавших в каждый из 5-ти определенных на предыдущем этапе интервалов, заключается в следующем: вводятся 5 колонок, соответствующих каждому из 5 интервалов; для каждой точки определяется значение в каждой из колонок, равное 1, если точка попала в соответствующий интервал, и равное 0 в противном случае. Для реализации приведенной идеи необходимо выполнить следующие действия:

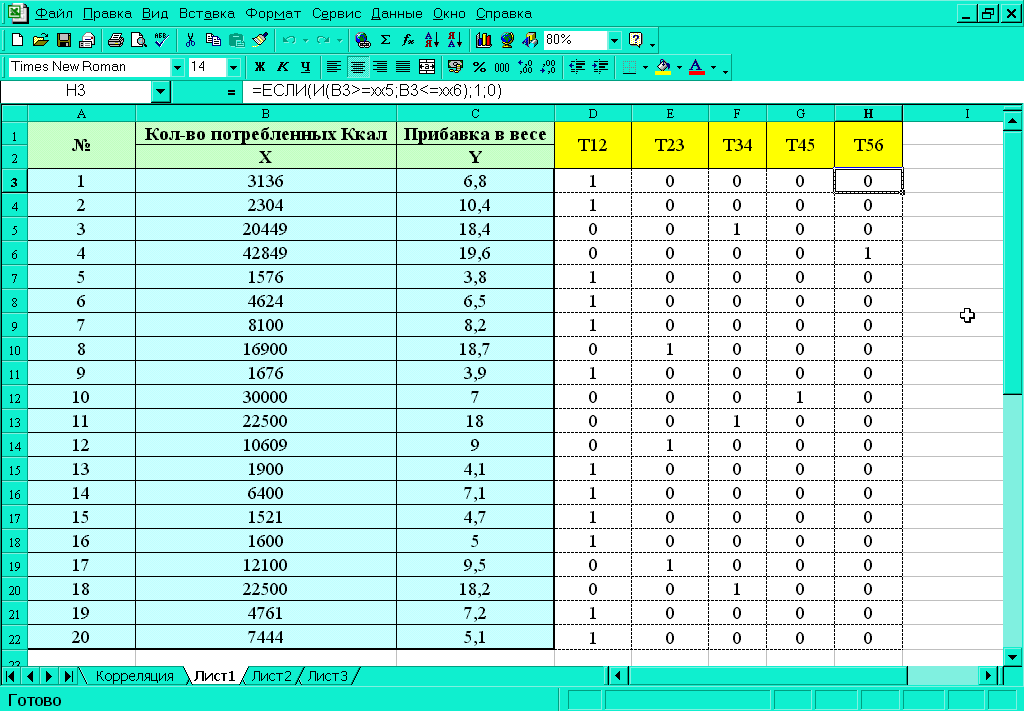
1) Ввести справа от колонки Прибавка в весе (Y) 5 колонок – Т12 (точки, попавшие в интервал [x1, x2]), Т23, Т34, Т45, Т56 (см. рисунок).

2) Заполнить колонку Т12 следующим образом:

• в ячейку, расположенную под Т12, ввести с использованием логических функций ЕСЛИ и И формулу, определяющую, попала ли точка 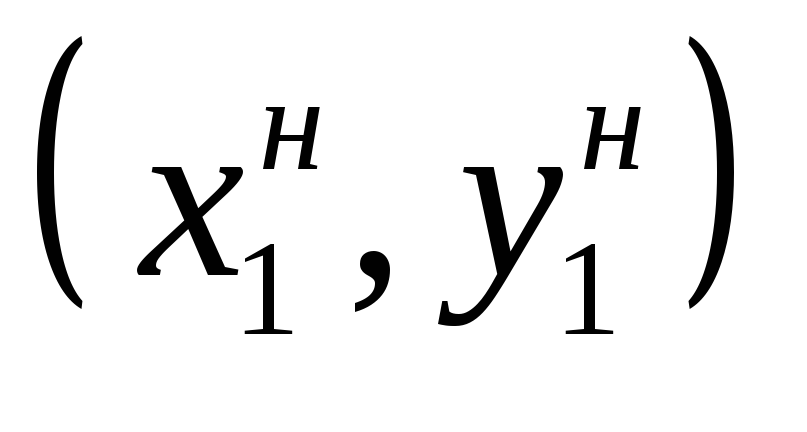в интервал [x1, x2]:

ЕСЛИ >=xx1 И <xx2, ТО Т12 = 1, ИНАЧЕ Т12 = 0

Вид набираемой формулы см. на следующем рисунке.

• скопировать введенную формулу в ячейки D4:D22, получив значения для всех точек 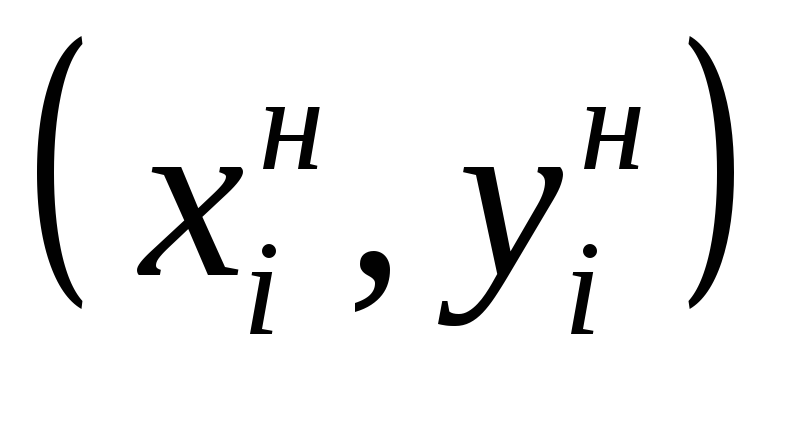; результат см. на рисунке в столбце D(Т12).

3) Аналогично колонке Т12 заполнить остальные колонки (Т23, Т34, Т45, Т56), изменяя только в формулах обозначения границ интервалов:

ЕСЛИ >=xx2 И <xx3, ТО Т23 = 1, ИНАЧЕ Т23 = 0

ЕСЛИ >=xx3 И <xx4, ТО Т34 = 1, ИНАЧЕ Т34 = 0

ЕСЛИ >=xx4 И <xx5, ТО Т45 = 1, ИНАЧЕ Т45 = 0

ЕСЛИ >=xx5 И <=xx6, ТО Т56 = 1, ИНАЧЕ Т56 = 0

Таким образом каждой точке соответствует только одно значение, равное 1, определяющее в какой интервал попала эта точка.