Лабораторная работа 6

Составление динамической модели простейшей механической колебательной системы методом электромеханических аналогий

Цель работы: усвоение методики и развитие навыков выполнения начальных процедур анализа акустических систем: составление динамической модели анализируемого устройства, составление его эквивалентных электрических схем.

Методические указания к выполнению работы

Изучив материал по теме, выполнить задания, ответы на которые представить для отчета в письменном виде.

Введение

П ростейшая механическая колебательная система, состоящая из массы m, подвешенной на пружине, с коэффициентом гибкости с и внутренним трением r, является составной частью всех электроакустических аппаратов – громкоговорителей, микрофонов, телефонов и др.

Масса m реализуется в виде жесткой конической или куполообразной диафрагмы с подклеенной к ней звуковой катушкой.

П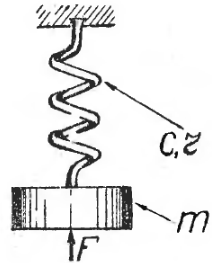 ружина имеет вид гофрированного кольца, называемого воротником, центрирующей шайбой или просто гофром.

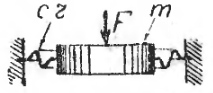
В упрощенном виде простейшую механическую колебательную систему в виде диска (поршня), подвешенного на гофрированной (а) или спиральной (б) пружине.

а) б)

Существует общность математических уравнений, которыми описываются колебания в механических системах и колебания тока в электрических цепях. Это ясно видно на примере уравнения напряжений, описывающего вынужденные колебания в одиночном линейном электрическим контуре, и уравнением сил для линейной механической колебательной системы с одной степенью свободы:

• электрическая цепь ,

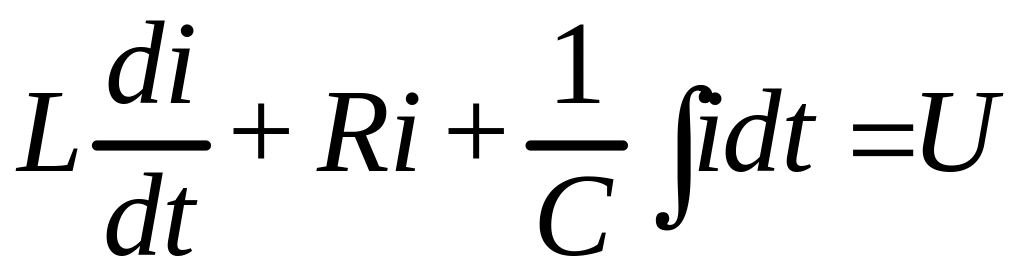• механическая система .

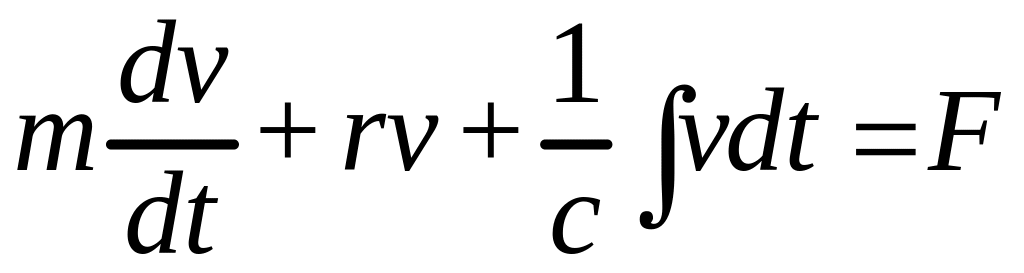С математической точки зрения эти уравнения ничем не отличаются. разница только в использованных обозначениях.

1 Механическая колебательная система с одной степенью свободы

Всякий акустический аппарат предста­вляет собой динамическую систему, в которой тем или иным способом возбуждаются колебания. Одним из таких способов, с которым чаще всего встречаются в технической акустике, является воздействие внешней периодической силы F.

Линейные колебательные системы ха­рактеризуются тем, что происходящие в них при этом вынужденные колебания имеют ча­стоту, совпадающую с частотой внешнего воз­действия. Такие системы называются линейными в силу того обстоятельства, что их поведение описывается линейными дифференциальными уравнениями. Значение линейных систем в тех­нической акустике связано с требованием не­искажённого преобразования колебаний из одних форм другие, а этому требованию могут удовле­творить только линейные системы.

П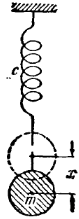 ростейший пример линейной механической колебатель­ной системы с одной степенью свободы – тело массой т, упруго связанное с положением равновесия, которое может перемещаться без тре­ния вдоль некоторой прямой представлен на рис. 1.

Такая система линейна, если возвращающая сила пропорциональна смещению тела х из положения равновесия:

возвр. сила = .

Знак «минус» указывает, что сила направлена противоположно смещению, поэтому она и называется возвращающей.

Рисунок 1

Коэф­фициенты и с характеризуют упругость и гибкость си­стемы. Упругость численно равна силе, вызывающей единич­ное смещение, измеряется в Н/м; гибкость с определяет смещение, вызываемое единичной силой, измеряется в м/Н.

Уравнение собственных (свободных) колебаний системы запишем в виде

, или (1)

где 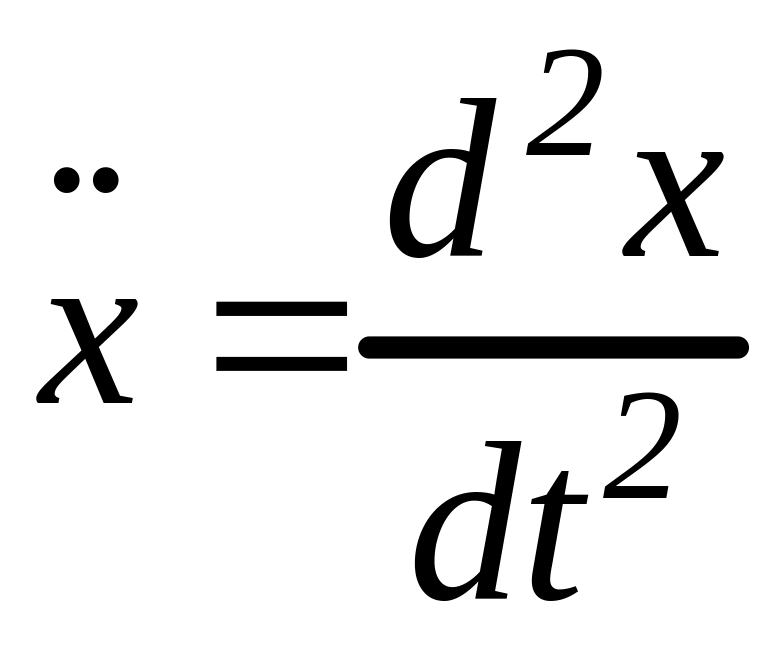– ускорение тела.

Уравнение движения (1) можно переписать иначе:

, (2)

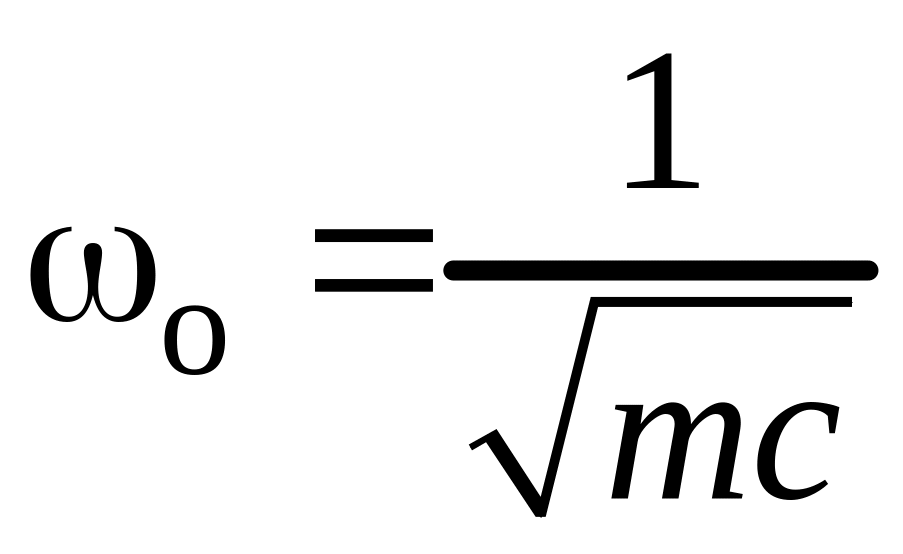где . (3)

Общее решение уравнения (2) записывается в комплексном виде как

, (4, а)

а в тригонометрическом виде как: , (4, б)

где – произвольные постоянные.

Решение по­казывает, что система, возбуждённая начальным толчком и затем предоставленная самой себе, совершает простое гар­моническое (незатухающее) колебание, круговая частота ( ) которого определяется по формуле (3) параметрами системы – её массой и гибкостью. Амплитуда колебания С и начальная фаза произвольны и зависят от начальных условий.

Практически свободные колебания будут, конечно, зату­хать благодаря неизбежному наличию рассеяния энергии. Желая подчеркнуть это обстоятельство, такую систему называют диссипативной.

В линейных системах диссипативные силы (силы сопротивления) пропорциональны скорости движения: , т.е. диссип. сила = – .

Знак минус указывает, что сила направлена к уменьшению скорости. Коэффициент r, численно равный диссипативной силе при единичной скорости, измеряется в Н·с/м и называется активным сопротивлением (физический смысл – коэффициент трения).

Уравнение свободных колебаний диссипативной системы имеет вид

– или = 0 . (6)

Разделив на m и введя дополнительные обозначения = , получим:

= 0 . (7)

Величина = называется коэффициент затухания.

Если линейная система совершает вынужденные колебания под действием внешней периодической синусоидальной силы F, уравнение движения можно представить в виде:

= . (10)

Общее решение уравнения (10) складывается из двух частей:

. (11)

Здесь – собственное затухающее колебание, прекращающееся через некоторый промежуток времени; – вынужденное (стационарное) колебание под действием внешней силы с частотой .

Если решение уравнения представить в виде , то подстановка в уравнение (10) даёт: . Отсюда

.

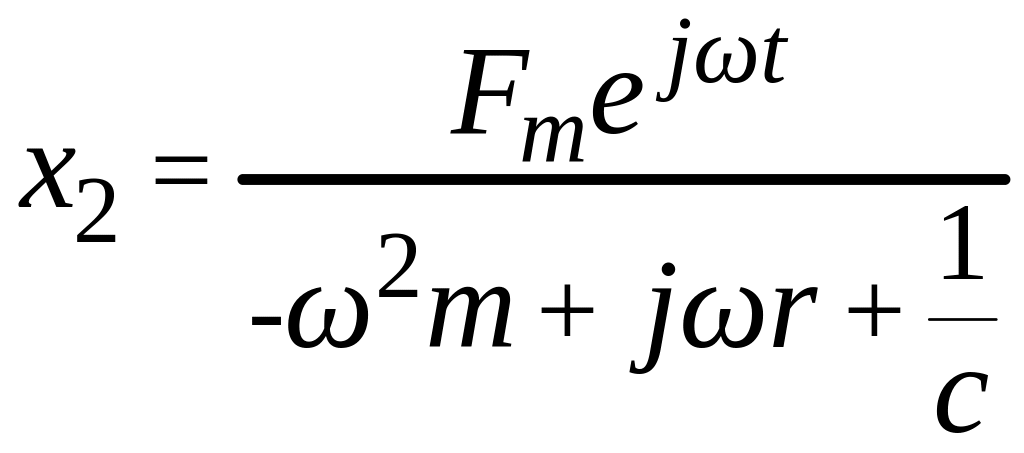Интересным является определение скорости вынужденного колебательного движения: 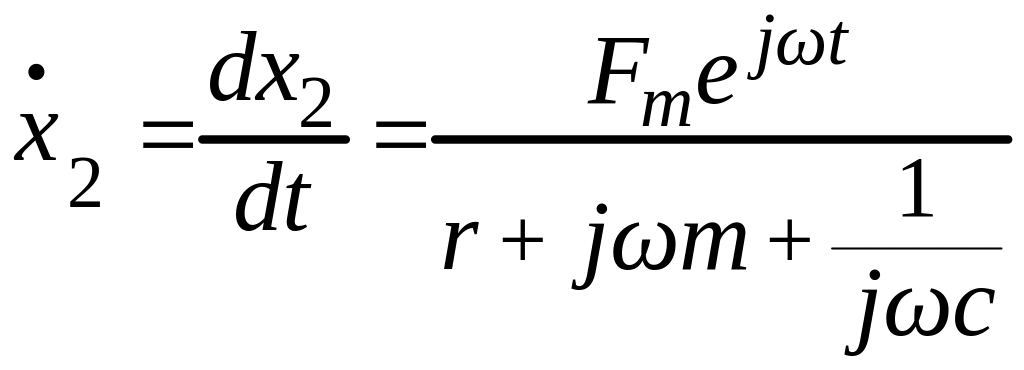. Амплитуда скорости вынужденных колебаний будет равна:

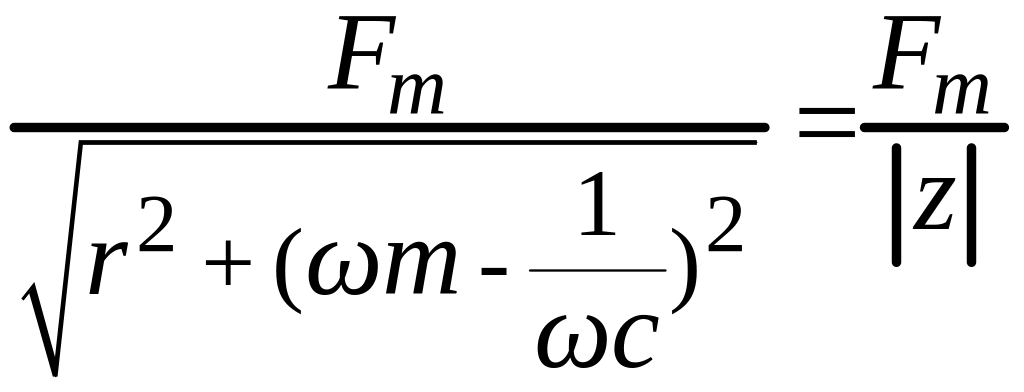= . (12)

Анализ полученного выражения показывает, что при заданной амплитуде внешней силы, амплитуда скорости вынужденных колебаний зависит от:

1. параметров системы m, c, r,

2. частоты внешнего воздействия.

Величина = = называется полным механическим сопротивлением системы.

В комплексной форме механическое сопротивление линейной системы с одной степенью свободы записывается в виде:

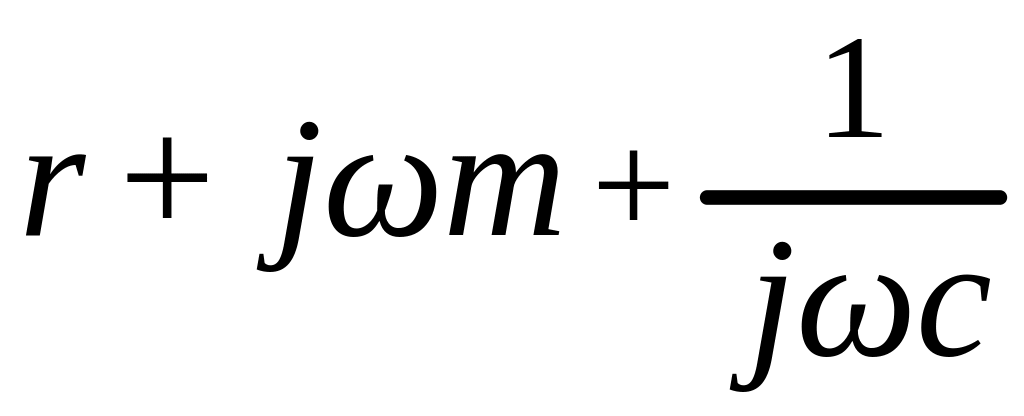= . (13)

Компонентами механического сопротивления линейной системы с одной степенью свободы являются:

- инерциальное сопротивление

- упругое сопротивление (14)

- активное сопротивление .

Частота , при которой инерциальное сопротивление полностью компенсируется упругим сопротивлением, т.е.

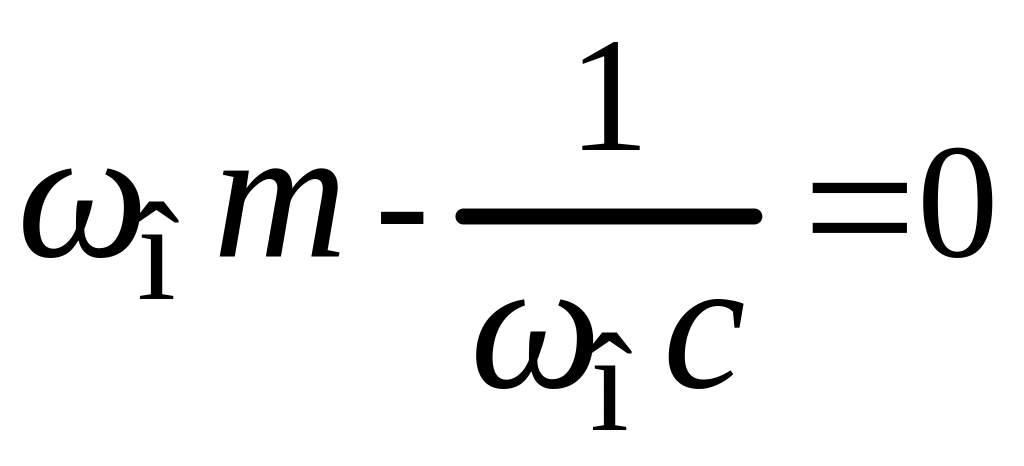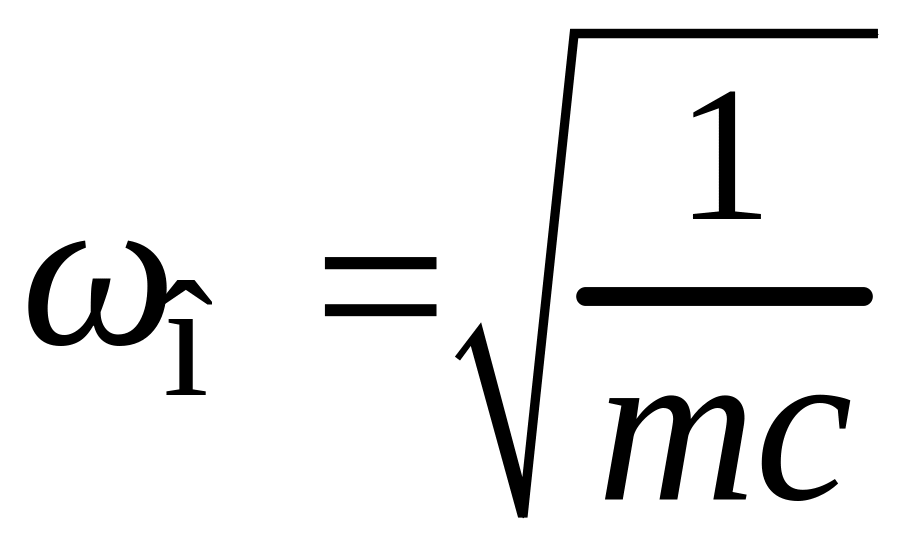, (15)

называется резонансной. На этой частоте скорость имеет наибольшее значение.

Выражения (12) позволяют построить частотные зависимости амплитуд смещения, скорости и ускорения простой колебательной системы. Эти зависимости удобно строить, пользуясь безразмерными представлениями, т.е. отнеся каждую из интересующих величин к какому-нибудь наиболее характерному её значению, или иначе говоря, пронормировав её по этому значению.

Например, вместо круговой частоты удобно пользоваться безразмерной величиной , для чего следует пронормировать по резонансной частоте : . При этом резонансу соответствует значение =1.

Механическое сопротивление также можно представить в безразмерном (нормированном) виде. На резонансной частоте инерциальное ( ) и упругое ( ) сопротивления имеют одинаковую величину. При этом каждое из них равно так называемому характеристическому сопротивлению колебательной системы: .

Действительно, воспользовавшись формулой (15), можно проделать следующее преобразование:

.

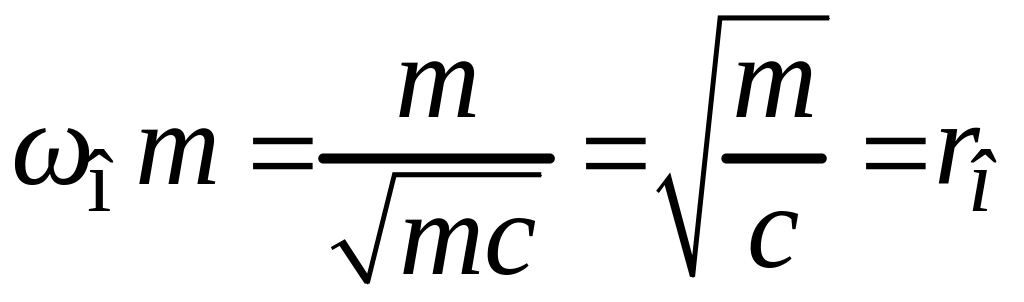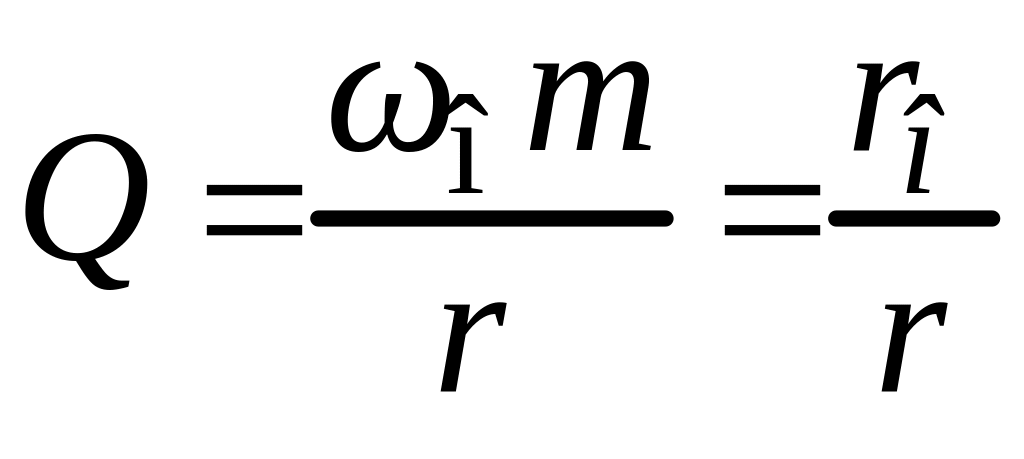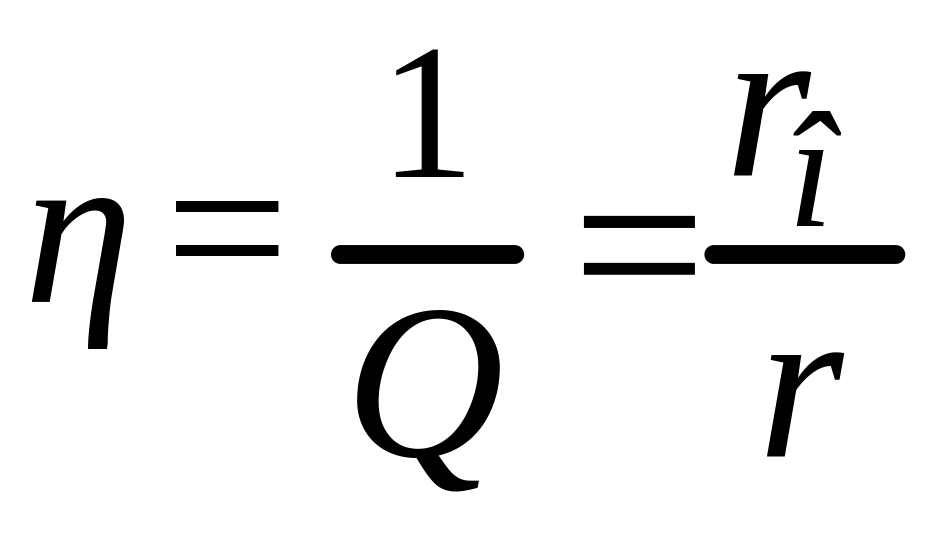Величина является удобным нормирующим коэффициентом для механического сопротивления. При нормировании по появляется отношение вида , называемое добротностью системы. Обратная ей величина, т.е. называется коэффициентом потерь.

Разбив диапазон изменения частоты на три области: ( >1), ( <1) и ( ~1) можно рассмотреть некоторые частные случаи механической системы с одной степенью свободы.

1) Система, управляемая массой. Получается в тех случаях, когда инерциальное сопротивление значительно преобладает над упругим и активным, т.е. ; .

С учетом (3) первое неравенство приводится к виду . С учетом (7) второе неравенство приводится к виду: .

Вывод. Если система имеет низкую собственную частоту и малое затухание, то из числа параметров системы преобладающее значение имеет масса. Полное сопротивление мало отличается от инерциального: ~ ,

; ; ,

т.е. в таком режиме частотно независимым является ускорение.

2) Система, управляемая упругостью. Реализуется при условиях

; ,

или, что то же самое, ; . Последнее неравенство означает, что постоянная времени мала по сравнению с периодом внешней силы. Характерной особенностью такой системы является независимость от частоты ее смещения; скорость и ускорение пропорциональны соответственно первой и второй степени частоты.

Вывод. В системе с высокой собственной частотой преобладающее значение имеет гибкость (или обратная ей величина – упругость). Полное сопротивление мало отличается от упругого: ~ .

3) Система, управляемая сопротивлением.. Характеризуется преобладанием активного сопротивления над реактивным: ~ .

Это случай либо апериодической системы ( , ), либо системы, возбуждаемой частотами, близкими к резонансной частоте, когда реактивное сопротивление мало благодаря взаимной компенсации инерциального и упругого сопротивления: – ~ 0.