
- •Компьютерный практикум
- •1. Типы роста и трендовые модели
- •2. Множественная регрессия
- •Independent variable list – независимые переменные )
- •3. Обобщенный регрессионный анализ
- •4. Регрессионные модели
- •5. Регрессионные модели
- •6. Авторегрессионные процессы и их модели
- •7. Адаптивные модели прогнозирования
- •Объем продаж новых автомобилей в сша, шт.
- •8. Прогнозирование сезонных колебаний
7. Адаптивные модели прогнозирования
Пример
11. В табл.
48 (см. также рис. 35) приведены данные о
ежемесячном спросе на бензин (![]() )
в компании Yukong
Oil
из Южной Кореи за период с января 1992г.
по июнь 1996г.2
Требуется построить предиктор Хольта
для расчета прогнозных оценок спроса
на бензин в ближайшие три месяца.
)
в компании Yukong
Oil
из Южной Кореи за период с января 1992г.
по июнь 1996г.2
Требуется построить предиктор Хольта
для расчета прогнозных оценок спроса
на бензин в ближайшие три месяца.
Т а б л и ц а 48
Ежемесячный спрос на бензин (тыс. баррелей/день) в компании Yukong Oil
|
Год |
Месяц |
|
Год |
Месяц |
|
Год |
Месяц |
|
|
1992 |
Январь |
82,3 |
1993 |
Июль |
113,5 |
1995 |
Январь |
145,8 |
|
Февраль |
83,6 |
Август |
120,4 |
Февраль |
144,4 |
|||
|
Март |
85,5 |
Сентябрь |
124,6 |
Март |
154,2 |
|||
|
Апрель |
91,0 |
Октябрь |
116,7 |
Апрель |
148,6 |
|||
|
Май |
92,1 |
Ноябрь |
120,6 |
Май |
153,7 |
|||
|
Июнь |
95,8 |
Декабрь |
124,9 |
Июнь |
157,9 |
|||
|
Июль |
98,3 |
1994 |
Январь |
122,2 |
Июль |
169,7 |
||
|
Август |
102,2 |
Февраль |
121,4 |
Август |
184,2 |
|||
|
Сентябрь |
101,5 |
Март |
125,6 |
Сентябрь |
163,2 |
|||
|
Октябрь |
98,5 |
Апрель |
129,7 |
Октябрь |
155,4 |
|||
|
Ноябрь |
101,1 |
Май |
133,6 |
Ноябрь |
168,9 |
|||
|
Декабрь |
102,5 |
Июнь |
137,5 |
Декабрь |
178,3 |
|||
|
1993 |
Январь |
102,7 |
Июль |
143,0 |
1996 |
Январь |
170,0 |
|
|
Февраль |
102,2 |
Август |
149,0 |
Февраль |
176,3 |
|||
|
Март |
104,7 |
Сентябрь |
149,9 |
Март |
174,2 |
|||
|
Апрель |
108,9 |
Октябрь |
139,5 |
Апрель |
176,1 |
|||
|
Май |
112,2 |
Ноябрь |
147,7 |
Май |
185,3 |
|||
|
Июнь |
109,7 |
Декабрь |
154,7 |
Июнь |
182,7 |
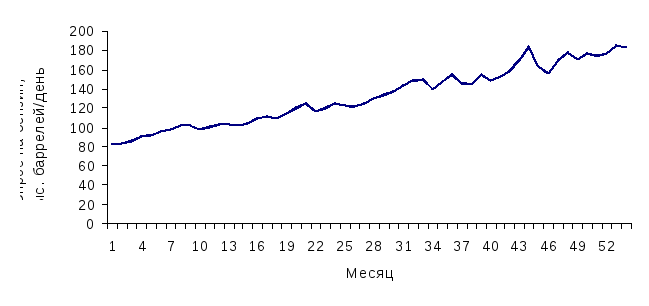
Рис. 35. Динамика спроса на бензин
Решение с помощью MS Excel
1.
Деление множества наблюдений на три
части: с 1 по 48 наблюдение будут использованы
для оценки параметров адаптивного
полинома первой степени; с 49 по 51 – для
настройки параметра
![]() ;
с 52 по 54 – для проверки предикторной
точности модели.
;
с 52 по 54 – для проверки предикторной
точности модели.
2. Определение начальных значений коэффициентов модели
![]() ,
,
![]()
и задание начальных значений параметров экспоненциального сглаживания
![]() ,
,
![]() .
.
3. Расчет текущих значений коэффициентов предиктора Хольта


Оформление результатов этих расчетов в виде табл. 49.
Т а б л и ц а 49
Текущие значения коэффициентов предиктора Хольта
|
|
|
|
|
|
|
|
|
|
|
1 |
82,30 |
1,30 |
17 |
109,94 |
1,63 |
33 |
141,47 |
2,04 |
|
2 |
83,60 |
1,30 |
18 |
111,39 |
1,62 |
34 |
143,11 |
2,00 |
|
3 |
84,96 |
1,31 |
19 |
113,05 |
1,62 |
35 |
145,37 |
2,03 |
|
4 |
86,74 |
1,35 |
20 |
115,24 |
1,68 |
36 |
148,13 |
2,10 |
|
5 |
88,49 |
1,39 |
21 |
117,69 |
1,75 |
37 |
149,79 |
2,06 |
|
6 |
90,48 |
1,45 |
22 |
119,17 |
1,73 |
38 |
151,10 |
1,98 |
|
7 |
92,57 |
1,52 |
23 |
120,87 |
1,72 |
39 |
153,19 |
1,99 |
|
8 |
94,90 |
1,60 |
24 |
122,82 |
1,75 |
40 |
154,53 |
1,93 |
|
9 |
96,99 |
1,65 |
25 |
124,33 |
1,72 |
41 |
156,18 |
1,90 |
|
10 |
98,63 |
1,65 |
26 |
125,59 |
1,68 |
42 |
158,06 |
1,90 |
|
11 |
100,36 |
1,65 |
27 |
127,10 |
1,66 |
43 |
160,93 |
1,99 |
|
12 |
102,06 |
1,66 |
28 |
128,85 |
1,67 |
44 |
165,05 |
2,21 |
|
13 |
103,62 |
1,65 |
29 |
130,83 |
1,70 |
45 |
166,85 |
2,17 |
|
14 |
104,96 |
1,62 |
30 |
133,03 |
1,75 |
46 |
167,66 |
2,03 |
|
15 |
106,39 |
1,60 |
31 |
135,60 |
1,83 |
47 |
169,61 |
2,02 |
|
16 |
108,08 |
1,61 |
32 |
138,59 |
1,95 |
48 |
172,30 |
2,09 |
4.
Определение оптимальных значений
параметров сглаживания, для чего
используется группа наблюдений, которые
были выделены для этих целей. С помощью
построенного адаптивного полинома
получим прогнозные оценки для
![]()
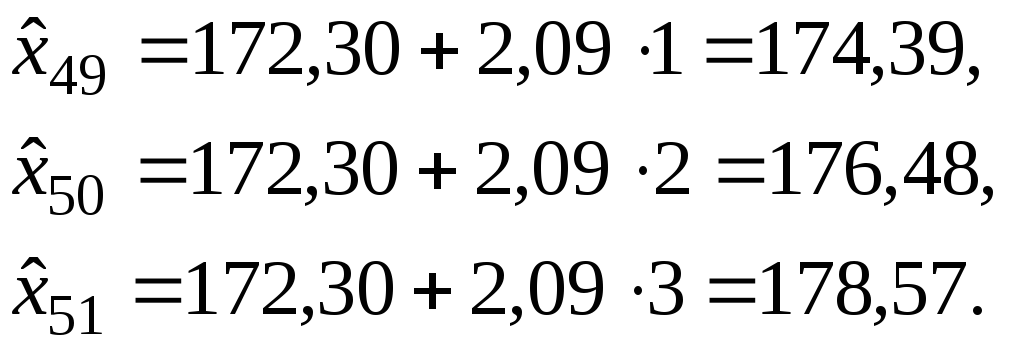
Вычислим относительные прогнозные ошибки

Путем
изменения параметров сглаживания
определим те его значения
![]() и
и
![]() ,
при которых максимальная относительная
ошибка станет минимальной. Оптимальными
значениями в нашем случае оказались
,
при которых максимальная относительная
ошибка станет минимальной. Оптимальными
значениями в нашем случае оказались
![]() и
и
![]() ,
при которых относительные ошибки
соответственно равны –1,29%; 1,27%; –1,00%.
,
при которых относительные ошибки
соответственно равны –1,29%; 1,27%; –1,00%.
5. Пересчет табл. 49 с использованием оптимальных значений параметров сглаживания (см. табл. 50).
Т а б л и ц а 50
Текущие значения коэффициентов предиктора Хольта
при оптимальных значениях параметров сглаживания
|
|
|
|
|
|
|
|
|
|
|
1 |
82,30 |
1,30 |
18 |
110,25 |
1,47 |
35 |
143,65 |
1,73 |
|
2 |
83,60 |
1,30 |
19 |
111,90 |
1,47 |
36 |
146,32 |
1,77 |
|
3 |
84,96 |
1,30 |
20 |
114,07 |
1,50 |
37 |
147,86 |
1,76 |
|
4 |
86,74 |
1,32 |
21 |
116,48 |
1,54 |
38 |
149,10 |
1,74 |
|
5 |
88,46 |
1,34 |
22 |
117,88 |
1,53 |
39 |
151,18 |
1,76 |
|
6 |
90,40 |
1,36 |
23 |
119,53 |
1,54 |
40 |
152,50 |
1,74 |
|
7 |
92,41 |
1,39 |
24 |
121,45 |
1,55 |
41 |
154,19 |
1,74 |
|
8 |
94,64 |
1,42 |
25 |
122,93 |
1,55 |
42 |
156,12 |
1,74 |
|
9 |
96,61 |
1,44 |
26 |
124,17 |
1,54 |
43 |
159,05 |
1,79 |
|
10 |
98,10 |
1,44 |
27 |
125,69 |
1,54 |
44 |
163,17 |
1,88 |
|
11 |
99,70 |
1,45 |
28 |
127,48 |
1,55 |
45 |
164,87 |
1,88 |
|
12 |
101,28 |
1,46 |
29 |
129,48 |
1,56 |
46 |
165,62 |
1,83 |
|
13 |
102,73 |
1,46 |
30 |
131,69 |
1,59 |
47 |
167,59 |
1,84 |
|
14 |
103,99 |
1,45 |
31 |
134,25 |
1,63 |
48 |
170,32 |
1,87 |
|
15 |
105,37 |
1,45 |
32 |
137,19 |
1,68 |
49 |
171,97 |
1,86 |
|
16 |
107,02 |
1,45 |
33 |
139,98 |
1,73 |
50 |
174,08 |
1,87 |
|
17 |
108,85 |
1,47 |
34 |
141,48 |
1,72 |
51 |
175,78 |
1,87 |
6. Проверка прогностических свойств модели на данных контрольной выборки

Таким образом, построенная модель позволяет получать прогнозные оценки достаточно высокой точности.
7. Получение модели для проведения прогнозных расчетов на три периода
![]() ,
,
![]() ,
,
для чего необходимо досчитать табл. 60, используя контрольные наблюдения.
8. Получение прогнозных оценок
![]()
![]()
![]()
и построение графиков фактических и расчетных значений (см. рис. 36).

Рис. 36. Прогнозирование спроса на бензин с помощью модели Ч. Хольта
Решение с помощью STATISTICA
-
Ввод исходных данных.
-
Вызов модуля «Прогноз/Серия времени» (Статистика / Дополнительные Линейные/Нелинейные модели / Прогноз/Серия времени).
-
Выбор переменной для анализа (Variables / Var1, см. рис. 37).

Рис. 37. Выбор переменных для анализа
-
Переход на вкладку Seasonal and Non-Seasonal Exponential Smoothing (Сезонное и несезонное экспоненциальное сглаживание, см. рис. 38). С целью получения результатов, идентичных результатам, полученным в MS Excel, необходимо выбрать: Linear Trend: Holt (Линейный тренд: Хольт); Alpha (Альфа) – 0,01; Gamma (Гамма) – 0,04; User-def. initial value (Начальное значение, выбираемое пользователем) – 82,3; Initial trend (Начальный тренд) – 1,3; Forecast (Прогнозировать) – 3 cases (наблюдения). Далее следует нажать на кнопку «Summary: Exponential smoothing» («Результаты анализа: Экспоненциальное сглаживание»), появится окно с таблицей, аналогичной табл. 51.

Рис. 38. Вкладка Seasonal and Non-Seasonal Exponential Smoothing
(Сезонное и несезонное экспоненциальное сглаживание)
Т а б л и ц а 51
Результаты анализа: Экспоненциальное сглаживание
|
№ |
Фактические значения |
Сглаженные значения |
Остатки |
№ |
Фактические значения |
Сглаженные значения |
Остатки |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1. |
82,3000 |
83,6000 |
-1,3000 |
30. |
137,5000 |
130,8102 |
6,6898 |
|
2. |
83,6000 |
84,7648 |
-1,1648 |
31. |
143,0000 |
133,0425 |
9,9575 |
|
3. |
85,5000 |
85,9385 |
-0,4385 |
32. |
149,0000 |
135,6414 |
13,3586 |
|
4. |
91,0000 |
87,1830 |
3,8170 |
33. |
149,9000 |
138,6339 |
11,2661 |
|
5. |
92,1000 |
88,8684 |
3,2316 |
34. |
139,5000 |
141,4622 |
-1,9622 |
|
6. |
95,8000 |
90,5081 |
5,2919 |
35. |
147,7000 |
142,9598 |
4,7402 |
|
7. |
98,3000 |
92,3750 |
5,9250 |
36. |
154,7000 |
145,1466 |
9,5534 |
|
8. |
102,2000 |
94,3290 |
7,8710 |
37. |
145,8000 |
147,8529 |
-2,0529 |
|
9. |
101,5000 |
96,5090 |
4,9910 |
38. |
144,4000 |
149,3904 |
-4,9904 |
|
10. |
98,5000 |
98,4210 |
0,0790 |
39. |
154,2000 |
150,6142 |
3,5858 |
|
11. |
101,1000 |
99,8421 |
1,2579 |
40. |
148,6000 |
152,7100 |
-4,1100 |
|
12. |
102,5000 |
101,3862 |
1,1138 |
41. |
153,7000 |
154,0197 |
-0,3197 |
Окончание табл. 51
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
13. |
102,7000 |
102,9202 |
-0,2202 |
42. |
157,9000 |
155,7072 |
2,1928 |
|
14. |
102,2000 |
104,3200 |
-2,1200 |
43. |
169,7000 |
157,6547 |
12,0453 |
|
15. |
104,7000 |
105,5214 |
-0,8214 |
44. |
184,2000 |
160,6356 |
23,5644 |
|
16. |
108,9000 |
106,8493 |
2,0507 |
45. |
163,2000 |
164,8627 |
-1,6627 |
|
17. |
112,2000 |
108,4726 |
3,7274 |
46. |
155,4000 |
166,5604 |
-11,160 |
|
18. |
109,7000 |
110,2785 |
-0,5785 |
47. |
168,9000 |
167,2638 |
1,6362 |
|
19. |
113,5000 |
111,6515 |
1,8485 |
48. |
178,3000 |
169,2533 |
9,0467 |
|
20. |
120,4000 |
113,2746 |
7,1254 |
49. |
170,0000 |
172,0201 |
-2,0201 |
|
21. |
124,6000 |
115,4539 |
9,1461 |
50. |
176,3000 |
173,6721 |
2,6279 |
|
22. |
116,7000 |
117,8718 |
-1,1718 |
51. |
174,2000 |
175,7994 |
-1,5994 |
|
23. |
120,6000 |
119,2533 |
1,3467 |
52. |
176,1000 |
177,4976 |
-1,3976 |
|
24. |
124,9000 |
120,8920 |
4,0080 |
53. |
185,3000 |
179,2104 |
6,0896 |
|
25. |
122,2000 |
122,8129 |
-0,6129 |
54. |
182,7000 |
181,6962 |
1,0038 |
|
26. |
121,4000 |
124,2692 |
-2,8692 |
Прогнозные значения |
|||
|
27. |
125,6000 |
125,4884 |
0,1116 |
55. |
|
183,6775 |
|
|
28. |
129,7000 |
127,0061 |
2,6939 |
56. |
|
185,5585 |
|
|
29. |
133,6000 |
128,7929 |
4,8071 |
57. |
|
187,4394 |
|
Как видно из табл. 51, прогнозные значения, полученные в STATISTICA, мало отличаются от значений, рассчитанных в Excel. Однако в STATISTICA предусмотрено больше возможностей по автоматическому оцениванию начальных значений и поиску оптимальных параметров. Чтобы ими воспользоваться необходимо:
-
перейти на вкладку Grid search (Поиск на сетке, см. рис. 39). Здесь надо задать узлы сетки, на которой происходит поиск параметров (Start parameter at – начать с параметра, Increment by – с шагом, Stop at – остановится на). Система переберет все значения параметров на заданной сетке и определит наилучшие значения, с которыми следует провести сглаживание;
-
щелкнуть по кнопке Perform grid search (Выполнить поиск на сетке). В результате появится таблица, представленная на рис. 40. В верхней строке таблица показаны лучшие значения параметров (Альфа = 0,1 и Гамма = 0,1) а также оцененные системой начальные значения S0 = 81,35 и T0 = 1,894. Кроме того, в таблице приведены значения шести критериев, по которым проводился поиск оптимальных параметров: Mean Error (Средняя ошибка), Mean Abs Error (Средняя абсолютная ошибка), Sum of Squares (Сумма квадратов), Mean Squares (Среднее квадратов), Mean % Error (Средний процент ошибки), Mean Abs % Error (Средний процент абсолютной ошибки). Заметим, что критерий («минимальное значение максимальной ошибки, в %»), который был использован при проведении расчетов в Excel, в системе STATISTICA не предусмотрен.

Рис. 39. Вкладка Grid search (Поиск на сетке)

Рис. 40. Таблица результатов поиска лучших параметров на сетке
3) вернуться на вкладку Seasonal and Non-Seasonal Exponential Smoothing (Сезонное и несезонное экспоненциальное сглаживание) и щелкнуть по кнопке «Summary: Exponential smoothing» («Результаты анализа: Экспоненциальное сглаживание»). В результате появится окно с таблицей, аналогичной табл. 52.
Т а б л и ц а 52
Результаты анализа: Экспоненциальное сглаживание
|
№ |
Фактические значения |
Сглаженные значения |
Остатки |
№ |
Фактические значения |
Сглаженные значения |
Остатки |
|
1. |
82,3000 |
83,2472 |
-0,9472 |
30. |
137,5000 |
133,1375 |
4,3625 |
|
2. |
83,6000 |
85,0373 |
-1,4373 |
31. |
143,0000 |
135,2433 |
7,7567 |
|
3. |
85,5000 |
86,7641 |
-1,2641 |
32. |
149,0000 |
137,7661 |
11,2339 |
|
4. |
91,0000 |
88,4955 |
2,5045 |
33. |
149,9000 |
140,7490 |
9,1510 |
|
5. |
92,1000 |
90,6289 |
1,4711 |
34. |
139,5000 |
143,6151 |
-4,1151 |
|
6. |
95,8000 |
92,6736 |
3,1264 |
35. |
147,7000 |
145,1134 |
2,5866 |
|
7. |
98,3000 |
94,9151 |
3,3849 |
36. |
154,7000 |
147,3078 |
7,3922 |
|
8. |
102,2000 |
97,2163 |
4,9837 |
37. |
145,8000 |
150,0567 |
-4,2567 |
|
9. |
101,5000 |
99,7273 |
1,7727 |
38. |
144,4000 |
151,5981 |
-7,1981 |
|
10. |
98,5000 |
101,9348 |
-3,4348 |
39. |
154,2000 |
152,7734 |
1,4266 |
|
11. |
101,1000 |
103,5873 |
-2,4873 |
40. |
148,6000 |
154,8254 |
-6,2254 |
|
12. |
102,5000 |
105,3096 |
-2,8096 |
41. |
153,7000 |
156,0500 |
-2,3500 |
|
13. |
102,7000 |
106,9716 |
-4,2716 |
42. |
157,9000 |
157,6386 |
0,2614 |
|
14. |
102,2000 |
108,4447 |
-6,2447 |
43. |
169,7000 |
159,4909 |
10,2091 |
|
15. |
104,7000 |
109,6580 |
-4,9580 |
44. |
184,2000 |
162,4401 |
21,7599 |
|
16. |
108,9000 |
110,9505 |
-2,0505 |
45. |
163,2000 |
166,7620 |
-3,5620 |
|
17. |
112,2000 |
112,5131 |
-0,3131 |
46. |
155,4000 |
168,5161 |
-13,1161 |
|
18. |
109,7000 |
114,2464 |
-4,5464 |
47. |
168,9000 |
169,1836 |
-0,2836 |
|
19. |
113,5000 |
115,5109 |
-2,0109 |
48. |
178,3000 |
171,1316 |
7,1684 |
|
20. |
120,4000 |
117,0088 |
3,3912 |
49. |
170,0000 |
173,8964 |
-3,8964 |
|
21. |
124,6000 |
119,0809 |
5,5191 |
50. |
176,3000 |
175,5158 |
0,7842 |
|
22. |
116,7000 |
121,4209 |
-4,7209 |
51. |
174,2000 |
177,6110 |
-3,4110 |
|
23. |
120,6000 |
122,6897 |
-2,0897 |
52. |
176,1000 |
179,2527 |
-3,1527 |
|
24. |
124,9000 |
124,2008 |
0,6992 |
53. |
185,3000 |
180,8886 |
4,4114 |
|
25. |
122,2000 |
125,9977 |
-3,7977 |
54. |
182,7000 |
183,3251 |
-0,6251 |
|
26. |
121,4000 |
127,3070 |
-5,9070 |
Прогнозные значения |
|||
|
27. |
125,6000 |
128,3462 |
-2,7462 |
55. |
|
185,2517 |
|
|
28. |
129,7000 |
129,6741 |
0,0259 |
56. |
|
187,2407 |
|
|
29. |
133,6000 |
131,2794 |
2,3206 |
57. |
|
189,2298 |
|
Заметим, что прогнозные значения в табл. 52 отличается от ранее полученных значений. Это объясняется тем, что расчеты проводились, во-первых, при разных начальных значениях, а во-вторых, при разных параметрах.
Пример 12. Требуется сравнить прогностические возможности предиктора Хольта с адаптивным полиномом Брауна. Для этого необходимо построим адаптивный полином по данным табл. 48.
Решение с помощью MS Excel
1.
Определение с помощью обычного МНК
коэффициенты
![]() и
и
![]() полинома
полинома
![]()
 ,
,
которые используются для расчета начальных значений экспоненциальных средних)
![]() ,
,
![]() .
.
Заметим,
что в качестве первоначального значения
параметра сглаживания было выбрано
![]() .
.
2. Расчет экспоненциальных средних первого и второго порядка


а также коэффициентов адаптивного полинома


Оформление результатов расчетов в виде табл. 53.
Т а б л и ц а 53
Экспоненциальные средние первого и второго порядка
и коэффициенты адаптивного полинома
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
77,87 |
73,47 |
82,28 |
1,89 |
25 |
120,53 |
117,08 |
123,99 |
1,48 |
|
2 |
79,59 |
75,31 |
83,88 |
1,84 |
26 |
120,79 |
118,19 |
123,39 |
1,11 |
|
3 |
81,36 |
77,12 |
85,61 |
1,82 |
27 |
122,23 |
119,40 |
125,07 |
1,21 |
|
4 |
84,25 |
79,26 |
89,25 |
2,14 |
28 |
124,47 |
120,93 |
128,02 |
1,52 |
|
5 |
86,61 |
81,47 |
91,75 |
2,20 |
29 |
127,21 |
122,81 |
131,61 |
1,89 |
|
6 |
89,37 |
83,84 |
94,90 |
2,37 |
30 |
130,30 |
125,06 |
135,54 |
2,25 |
|
7 |
92,05 |
86,30 |
97,79 |
2,46 |
31 |
134,11 |
127,77 |
140,44 |
2,72 |
Окончание табл. 53
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
8 |
95,09 |
88,94 |
101,25 |
2,64 |
32 |
138,58 |
131,01 |
146,14 |
3,24 |
|
9 |
97,01 |
91,36 |
102,67 |
2,42 |
33 |
141,97 |
134,30 |
149,64 |
3,29 |
|
10 |
97,46 |
93,19 |
101,73 |
1,83 |
34 |
141,23 |
136,38 |
146,08 |
2,08 |
|
11 |
98,55 |
94,80 |
102,31 |
1,61 |
35 |
143,17 |
138,42 |
147,93 |
2,04 |
|
12 |
99,74 |
96,28 |
103,19 |
1,48 |
36 |
146,63 |
140,88 |
152,38 |
2,46 |
|
13 |
100,63 |
97,58 |
103,67 |
1,30 |
37 |
146,38 |
142,53 |
150,23 |
1,65 |
|
14 |
101,10 |
98,64 |
103,56 |
1,05 |
38 |
145,79 |
143,51 |
148,07 |
0,98 |
|
15 |
102,18 |
99,70 |
104,66 |
1,06 |
39 |
148,31 |
144,95 |
151,67 |
1,44 |
|
16 |
104,19 |
101,05 |
107,34 |
1,35 |
40 |
148,40 |
145,98 |
150,81 |
1,03 |
|
17 |
106,60 |
102,71 |
110,48 |
1,66 |
41 |
149,99 |
147,18 |
152,79 |
1,20 |
|
18 |
107,53 |
104,16 |
110,90 |
1,44 |
42 |
152,36 |
148,74 |
155,99 |
1,55 |
|
19 |
109,32 |
105,71 |
112,93 |
1,55 |
43 |
157,56 |
151,39 |
163,74 |
2,65 |
|
20 |
112,64 |
107,79 |
117,50 |
2,08 |
44 |
165,55 |
155,64 |
175,47 |
4,25 |
|
21 |
116,23 |
110,32 |
122,14 |
2,53 |
45 |
164,85 |
158,40 |
171,30 |
2,76 |
|
22 |
116,37 |
112,14 |
120,61 |
1,82 |
46 |
162,01 |
159,48 |
164,54 |
1,08 |
|
23 |
117,64 |
113,79 |
121,49 |
1,65 |
47 |
164,08 |
160,86 |
167,30 |
1,38 |
|
24 |
119,82 |
115,60 |
124,04 |
1,81 |
48 |
168,35 |
163,11 |
173,58 |
2,24 |
3.
Определение оптимального значения
параметра сглаживания, для чего необходимо
использовать группу наблюдений, которые
были выделены для этих целей. Получение
с помощью построенного адаптивного
полинома прогнозных оценок для
![]()

и вычисление относительных прогнозных ошибок

Путем
изменения параметра сглаживания
определим то его значение
![]() ,
при котором максимальная относительная
ошибка станет минимальной. Оптимальным
значением оказалось
,
при котором максимальная относительная
ошибка станет минимальной. Оптимальным
значением оказалось
![]() ,
при котором относительные ошибки
соответственно равны –1,59%; 0,97%; –1,31%.
,
при котором относительные ошибки
соответственно равны –1,59%; 0,97%; –1,31%.
4. Пересчет табл.
53 для
![]() с целью контрольного прогнозного расчета
(см. табл. 54). Прогнозные расчеты на
контрольной выборке позволяют сделать
вывод, что прогностические возможности
предиктора Хольта и адаптивного полинома
Брауна практически не отличаются.
с целью контрольного прогнозного расчета
(см. табл. 54). Прогнозные расчеты на
контрольной выборке позволяют сделать
вывод, что прогностические возможности
предиктора Хольта и адаптивного полинома
Брауна практически не отличаются.
Т а б л и ц а 54
Экспоненциальные средние первого и второго порядка
и
коэффициенты адаптивного полинома при
оптимальном значении
![]()
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-104,27 |
-290,79 |
82,26 |
1,88 |
27 |
-55,48 |
-241,79 |
130,84 |
1,88 |
|
2 |
-102,39 |
-288,91 |
84,13 |
1,88 |
28 |
-53,62 |
-239,91 |
132,66 |
1,88 |
|
3 |
-100,51 |
-287,02 |
86,01 |
1,88 |
29 |
-51,75 |
-238,03 |
134,52 |
1,88 |
|
4 |
-98,59 |
-285,14 |
87,95 |
1,88 |
30 |
-49,86 |
-236,15 |
136,43 |
1,88 |
|
5 |
-96,69 |
-283,25 |
89,88 |
1,88 |
31 |
-47,93 |
-234,26 |
138,40 |
1,88 |
|
6 |
-94,76 |
-281,37 |
91,85 |
1,88 |
32 |
-45,96 |
-232,38 |
140,46 |
1,88 |
|
7 |
-92,83 |
-279,48 |
93,82 |
1,89 |
33 |
-44,00 |
-230,50 |
142,49 |
1,88 |
|
8 |
-90,88 |
-277,60 |
95,84 |
1,89 |
34 |
-42,17 |
-228,61 |
144,28 |
1,88 |
|
9 |
-88,96 |
-275,71 |
97,80 |
1,89 |
35 |
-40,27 |
-226,73 |
146,19 |
1,88 |
|
10 |
-87,08 |
-273,83 |
99,66 |
1,89 |
36 |
-38,32 |
-224,85 |
148,21 |
1,88 |
|
11 |
-85,20 |
-271,94 |
101,54 |
1,89 |
37 |
-36,48 |
-222,96 |
150,01 |
1,88 |
|
12 |
-83,32 |
-270,05 |
103,41 |
1,89 |
38 |
-34,67 |
-221,08 |
151,74 |
1,88 |
|
13 |
-81,46 |
-268,17 |
105,24 |
1,89 |
39 |
-32,78 |
-219,20 |
153,63 |
1,88 |
|
14 |
-79,63 |
-266,28 |
107,03 |
1,89 |
40 |
-30,97 |
-217,31 |
155,38 |
1,88 |
|
15 |
-77,78 |
-264,40 |
108,83 |
1,88 |
41 |
-29,12 |
-215,43 |
157,19 |
1,88 |
|
16 |
-75,92 |
-262,51 |
110,68 |
1,88 |
42 |
-27,25 |
-213,55 |
159,05 |
1,88 |
|
17 |
-74,04 |
-260,63 |
112,56 |
1,88 |
43 |
-25,28 |
-211,67 |
161,11 |
1,88 |
|
18 |
-72,20 |
-258,74 |
114,35 |
1,88 |
44 |
-23,19 |
-209,78 |
163,41 |
1,88 |
|
19 |
-70,34 |
-256,86 |
116,18 |
1,88 |
45 |
-21,32 |
-207,90 |
165,25 |
1,88 |
|
20 |
-68,43 |
-254,98 |
118,11 |
1,88 |
46 |
-19,56 |
-206,01 |
166,90 |
1,88 |
|
21 |
-66,50 |
-253,09 |
120,08 |
1,88 |
47 |
-17,67 |
-204,13 |
168,79 |
1,88 |
|
22 |
-64,67 |
-251,21 |
121,86 |
1,88 |
48 |
-15,71 |
-202,25 |
170,83 |
1,88 |
|
23 |
-62,82 |
-249,32 |
123,68 |
1,88 |
49 |
-13,85 |
-200,36 |
172,66 |
1,88 |
|
24 |
-60,94 |
-247,44 |
125,55 |
1,88 |
50 |
-11,95 |
-198,48 |
174,57 |
1,88 |
|
25 |
-59,11 |
-245,56 |
127,33 |
1,88 |
51 |
-10,09 |
-196,60 |
176,41 |
1,88 |
|
26 |
-57,31 |
-243,67 |
129,06 |
1,88 |
|
||||
5.
Построение графиков фактических и
расчетных значений ежемесячного спроса
на бензин (см. рис. 41). Заметим, что график
модели Р. Брауна, настроенной на получение
прогнозных оценок для
![]() ,
имеет вид прямой.
,
имеет вид прямой.

Рис. 41. Прогнозирование спроса на бензин с помощью модели Р. Брауна
Пример 13. Предположим, что президента холдинга «ВТД», интересует динамика числа акционеров. В частности, ему необходимо по данным предыдущих лет (см. табл. 55) построить модель для прогнозирования количества владельцев акций в зависимости от стоимости акции и размера дивидендов.
Т а б л и ц а 55
Динамика числа владельцев акций холдинг «ВТД» и влияющих на нее факторов
|
Год |
Количество владельцев акций, чел. |
Стоимость акции, тыс. руб. |
Дивиденды на одну акцию, тыс. руб. |
|
1995 |
26470 |
1,6 |
1,21 |
|
1996 |
28770 |
1,73 |
1,28 |
|
1997 |
29481 |
1,85 |
1,32 |
|
1998 |
31682 |
1,76 |
1,36 |
|
1999 |
30121 |
1,91 |
1,39 |
|
2000 |
31052 |
2,02 |
1,45 |
|
2001 |
30845 |
2,06 |
1,43 |
|
2002 |
32012 |
2,23 |
1,51 |
|
2003 |
32134 |
2,56 |
1,58 |
|
2004 |
32813 |
2,64 |
1,62 |
|
2005 |
33180 |
2,69 |
1,65 |
Решение с помощью MS Excel
1.
Определение начальные значения для
построения адаптивной регрессионной
модели
![]() и
и
![]() по первым восьми наблюдениям. Для этого:
по первым восьми наблюдениям. Для этого:
1) вычислим матрицу
![]() и найдем к ней обратную
и найдем к ней обратную
![]()
 ,
,
 .
.
2) сформируем вектор
![]() и получим начальные значения вектора
оценок коэффициентов адаптивной
регрессионной модели
и получим начальные значения вектора
оценок коэффициентов адаптивной
регрессионной модели
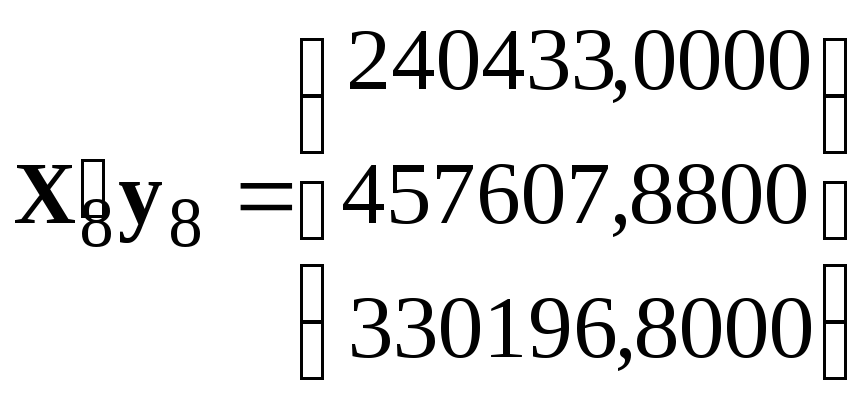 ,
,
 .
.
Таким образом, регрессионная модель с начальными значениями коэффициентов записывается в следующем виде:
![]() .
.
2. Осуществление
адаптивной корректировки коэффициентов
регрессионной модели в предположении,
что значение параметра сглаживания
![]() .
Для этого:
.
Для этого:
1) получим прогнозную
оценку
![]()
![]() ;
;
2) рассчитаем
![]()
 ;
;
3) вычислим
![]()
![]() ;
;
4) сформируем корректирующий вектор
 ;
;
5) рассчитаем прогнозную ошибку для вновь поступившего наблюдения
![]()
и умножим на эту ошибку корректирующий вектор
 ;
;
6) получим скорректированный по вновь поступившему наблюдению вектор коэффициентов адаптивной регрессионной модели
 .
.
Таким образом, регрессионная модель с обновленными коэффициентами имеет вид
![]() .
.
3. Настройка
параметра
![]() ,
для чего:
,
для чего:
-
рассчитаем прогнозную оценку
![]()
и соответствующую ошибку предсказания
![]() .
.
-
подберем параметр сглаживания таким образом, чтобы минимизировать ошибку. Минимальная по абсолютной величине ошибка
 была получены при
была получены при
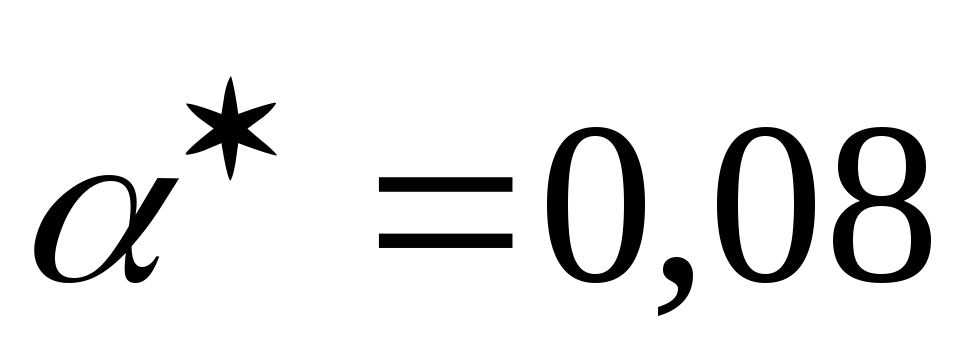 .
Оценки коэффициентов модели при таком
значении параметра сглаживания равны
.
Оценки коэффициентов модели при таком
значении параметра сглаживания равны
 .
.
4. Пересчет обратной матрицы

5. Корректировка
коэффициентов модели по 10-му наблюдению
с использованием полученной обратной
матрицы![]()

6. Пересчет обратной матрицы с учетом значения факторов 10-го наблюдения
 .
.
7. Корректировка
вектора оценок коэффициентов модели
таким же образом, как и на предыдущих
шагах, с использованием обратной матрицу
![]() и последнее (11-е) наблюдение.
и последнее (11-е) наблюдение.
В окончательном виде модель для прогнозирования количества владельцев акций холдинга записывается следующим образом:
![]() .
.
Пример 14. Предположим, что требуется разработать новый тариф на электроэнергию. Для этого необходимо построить модель для прогнозирования расходов населения на оплату электроэнергии в зависимости от размера потребления электроэнергии, цены 1 кВт/ч и количества потребителей. Данные для расчетов представлены в табл. 56.
Т а б л и ц а 56
Динамика расходов населения на электроэнергию и факторов на нее влияющих
|
Год |
Расходы на электро- энергию (млн. долл.) |
Потребление электроэнергии (кВт/ч) |
Цена электроэнергии (в центах за кВт/ч) |
Количество потребителей |
|
1974 |
25,8 |
12857 |
1,21 |
166588 |
|
1975 |
30,5 |
13843 |
1,29 |
170317 |
|
1976 |
33,3 |
14223 |
1,33 |
175536 |
|
1977 |
37,2 |
14427 |
1,42 |
181553 |
|
1978 |
42,5 |
14878 |
1,52 |
188325 |
|
1979 |
48,8 |
15763 |
1,59 |
194237 |
|
1980 |
55,4 |
15130 |
1,84 |
198847 |
|
1981 |
64,3 |
14697 |
2,17 |
201465 |
|
1982 |
78,9 |
15221 |
2,55 |
203444 |
|
1983 |
86,5 |
14166 |
2,97 |
205533 |
|
1984 |
114,6 |
14854 |
3,7 |
208574 |
|
1985 |
129,7 |
14997 |
4,1 |
210811 |
|
1986 |
126,1 |
13674 |
4,34 |
212865 |
|
1987 |
132,0 |
13062 |
4,71 |
214479 |
|
1988 |
138,1 |
13284 |
4,82 |
215610 |
|
1989 |
141,2 |
13531 |
4,81 |
217164 |
|
1990 |
143,7 |
13589 |
4,81 |
219968 |
|
1991 |
149,2 |
13800 |
4,84 |
223364 |
|
1992 |
146,1 |
13287 |
4,83 |
227575 |
|
1993 |
153,9 |
13406 |
4,91 |
233795 |
|
1994 |
146,9 |
12661 |
4,84 |
239733 |
|
1995 |
156,8 |
12434 |
4,98 |
253364 |
|
1996 |
158,2 |
12753 |
4,97 |
255771 |
|
1997 |
163,4 |
13678 |
5,1 |
258890 |
Решение с помощью MS Excel
1. Деление множества наблюдений на три части: с 1 по 18 наблюдение будем использовать для определения начальных значений; с 17 по 22 – для настройки параметра адаптации модели; 23 и 24 – для проведения контрольных прогнозных расчетов. Группу наблюдений для одновременной обработки будем формировать путем комбинирования наблюдений, которые уже участвовали в построении модели, и тех, которые еще не использовались, т.е. на первом шаге адаптации будут обрабатываться с 17 по 20 наблюдение, а на втором – с 19 по 22.
2. Определения начальных значений по первым 18 наблюдениям
 ,
, .
.
3. Проведение
промежуточных расчетов по корректировке
коэффициентов модели при
![]()
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;
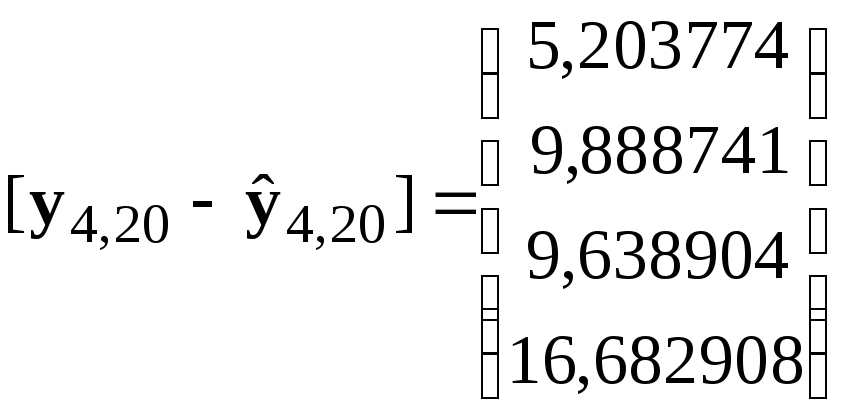 .
.
Получим окончательные значения корректирующего вектора:
 .
.
После первого шага адаптации вектор оценок коэффициентов модели выглядит следующим образом:
 .
.
4. Расчет постпрогнозных оценок
![]() ,
,
![]() ,
,
и их относительных ошибок
![]() ,
,
![]() .
.
5. Настройка
параметра адаптации
![]() ,
руководствуясь критерием «минимум
максимальной относительной ошибки», и
пересчет коэффициентов модели с этим
оптимальным значением
,
руководствуясь критерием «минимум
максимальной относительной ошибки», и
пересчет коэффициентов модели с этим
оптимальным значением
 .
.
6. Пересчет обратной
матрицы
![]() , используя 17 – 20 наблюдения
, используя 17 – 20 наблюдения

7. Выполнение расчетов, аналогичных тем, которые были проведены выше, но для наблюдений 19–22 и пересчитанной обратной матрице и получение скорректированного вектора оценок коэффициентов модели,

а также новой обратной матрице
 .
.
8. Проведение контрольных прогнозных расчетов, используя значения факторов в 23-м и 24-м наблюдениях
![]() ;
;
![]() .
.
Результаты расчетов свидетельствую о достаточно хороших прогностических свойствах модели.
9. Корректировка
вектора оценок коэффициентов модели
уже известным нам образом, используя
обратную матрицу
![]() и группу из последних четырех (с 20 по
24) наблюдений, в которую включена
контрольная выборка.
и группу из последних четырех (с 20 по
24) наблюдений, в которую включена
контрольная выборка.
В окончательном виде модель для прогнозирования расходов на оплату электроэнергии записывается следующим образом:
![]() .
.
Задание 12.
По данным табл. 57 для автомобиля марки
Ford
построить две модели: модель Хольта и
модель Брауна. Для обеих моделей провести
оптимальную настройку параметров
адаптации. Сравнить на контрольной
выборке из последних трех наблюдений
точность предсказания по этим моделям.
Осуществить прогнозные расчеты (![]() ),
используя более точную модель.
),
используя более точную модель.
Задание 13.
По данным табл. 57 для автомобилей Nissan
построить
прогнозную модель Хольта с адаптивным
механизмом Брауна и сравнить ее по
точности предсказания на контрольной
выборке из пяти последних наблюдений
с моделью в виде адаптивного полинома
Брауна первого порядка. Предусмотреть
оптимальную настройку параметров
сглаживания. По лучшей модели осуществить
прогноз объема продаж автомобилей этой
марки для
![]() .
.
Т а б л и ц а 57
