3 Исследование импульсной системы
3.1 Техническое задание
Wпг2(p)
Wгцн2(p)
Wпг2(p)
Wгцн2(p)
Wпг3(p)
Wгцн3(p)
Wпг4(p)
Wгцн4(p)
Wкд(p)
Рисунок 17 – Функциональная схема система
Из первоначальной линейной системы сделаем импульсную, для этого предположим, что передаточная функция первого элемента системы равна 1
3.2 Преобразование структурной схемы.
Преобразование структурной схемы:
Здесь и далее для расчетов и построения графиков воспользуемся программой MathCad.
Далее найдем выражение для общей передаточной функции:
Используя программу MathCAD, подставив значения функций, получим выражение общей передаточной функции:
3.3 Проведение z – преобразования
Для импульсных систем характерно построение решетчатых функций.
Для решетчатых функций времени может быть введено понятие дискретного преобразования Лапласа.
Для исследования импульсных систем большое распространение получило так называемое z-преобразование, которое связано с дискретным преобразованием Лапласа и вытекает из него.
Z-преобразование проведем по формуле:
(9)
где
и
- показатели аналого-цифрового
преобразователя и цифро-аналового
преобразователя. В рамках курсовой
работы принимает эти показатели равными
1;
-
передаточная функция импульсной системы.
3.4
Проведение
– преобразования
Для
проведения
– преобразования проведем замену.
Запишем передаточную функцию:
Построим весовую функцию.
Рисунок 18 – Весовая функция непрерывно-дискретной системы
3.5 Проведение λ- преобразования
Для проведения λ- преобразования введем замену.
где λ – псевдочастота.
Запишем передаточную функцию с учетом замены.
3.6 Построим ЛАЧХ и ЛФЧХ непрерывной дискретной части
Рисунок 19 – ЛАЧХ непрерывной дискретной системы
Рисунок 20 - ЛФЧХ непрерывно-дискретной системы
3.7 Определение устойчивости по Шур Кону
Определим устойчивость полученной импульсной системы по Шур Кону. Данный критерий позволяет анализировать устойчивость дискретных и дискретно-непрерывных систем по характеристическому уравнению замкнутой системы, записанному в форме z – преобразования. В нашем случае характеристическое уравнение имеет седьмую степень:
По уравнению запишем коэффициенты в виде определителя. Корни характеристического уравнения будут находиться внутри единичной окружности, если коэффициенты уравнения удовлетворяют всем определителям.
Проверим условия устойчивости по критерию Шур Кона для системы автоматического управления реакторной установки В – 320, рассматриваемой в данной курсовой работе.
Составим матрицу Шур Кона.
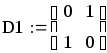
Посчитаем нечетные миноры матрицы. Для того, что бы система была устойчивой, чтобы нечетные миноры матрицы Шур Кона были меньше нуля, либо четные миноры матрицы были больше нуля.
Посчитав миноры в MathCAD, получили, что, нечетные миноры положительны, а четные миноры отрицательны.
Таким образом, получаем, что импульсная система неустойчива.