2. Моделирование аналоговой сау.

Для составления программы переходного процесса необходимо сначала промоделировать систему, применив различные методы.

Моделирование аналоговой САУ будем проводить последовательным моделированием начиная с первого звена и кончая последним при этом будем учитывать входные выходные сигналы а так же цепь обратной связи..

Для моделирования каждого звена из его передаточной функции выведем дифференциальное уравнение. Полученное дифференциальное уравнение приведём к нормальной форме Коши. Для решения дифференциальных уравнений воспользуемся методом приближённого интегрирования – методом трапеций (модифицированным методом Эйлера-Хьюна).

2.1. Алгоритм составления модели инерционного звена.

Передаточная функция инерционного звена имеет вид:

из принципа пропускания сигнала приравняем данное звено к отношению сигналов выхода к входу.

,

где - сигнал на выходе;

- сигнал на входе.

Представим выражение в следующем виде:

Получим следующее дифференциальное уравнение:

,

где - производная выходного сигнала по времени.

Проинтегрируем дифференциальное уравнение:

.

Представим решение в нормальной форме Коши:

.

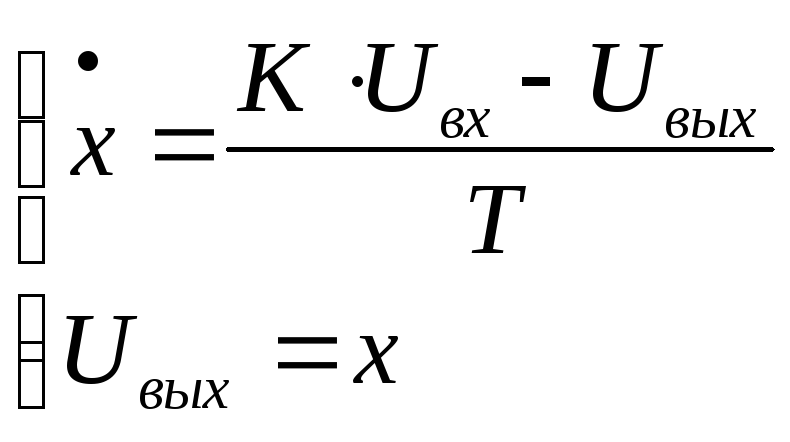При моделировании системы непрерывное течение процессов в реальной системе заменяется дискретным течением процессов в её модели. Значения функций вычисляются в моменты времени, кратные шагу времени.

Чтобы получить значение функции x, которая является фазовой координатой звена(промежуточным состояние системы), воспользуемся методом трапеций (модифицированным методом Эйлера).

2.2. Моделирование изодромного звена.

Передаточная функция изодромного звена имеет вид:

.

Приравняем передаточную функцию к отношению сигналов на входе и на выходе:

,

где - сигнал на выходе;

- сигнал на входе.

Представим выражение в следующем виде:

Получим следующее дифференциальное уравнение:

где - производная выходного сигнала по времени.

- производная входного сигнала по времени.

Проинтегрируем дифференциальное уравнение:

.

Представим решение в нормальной форме Коши:

Используя полученные модели напишем программу, используя среду Turbo Pascal, для построения переходного процесса.

3. Построение переходного процесса.

Для проверки правильности работы программы(Приложение) сравним результаты работы моделирующей программы с результатами моделирования в Simulink.

Аналоговая система и результаты её моделирования в пакете MatLab-Simulink.

Схема модели

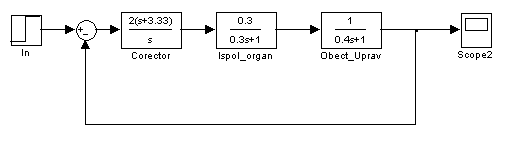
Аналоговая САР TurboPascalШаг времени Т=0,015

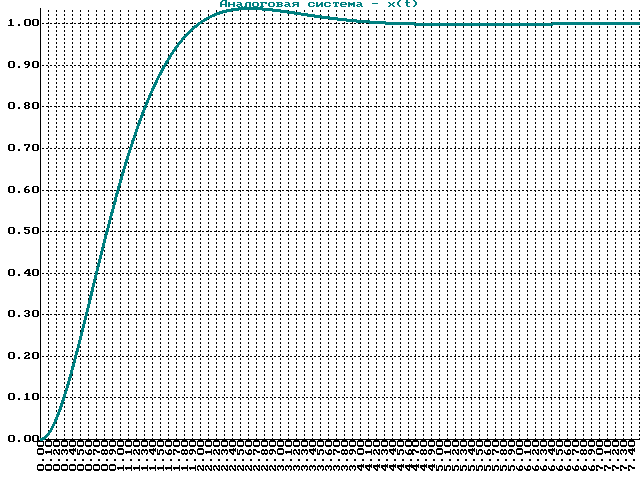
Simulink

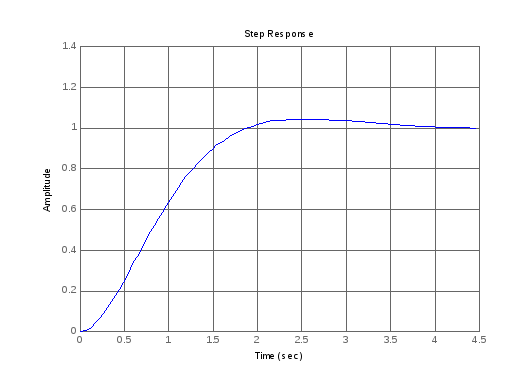
4. Исследование цифровой .Сау способом дискретизации непрерывного регулятора

4.1. Исследование сау с дискретизацией регулятора по способу Тастина.

Для этого найдем передаточную функцию цифрового корректирующего устройства, воспользовавшись преобразованием Тастина для дискретизации непрерывного регулятора.

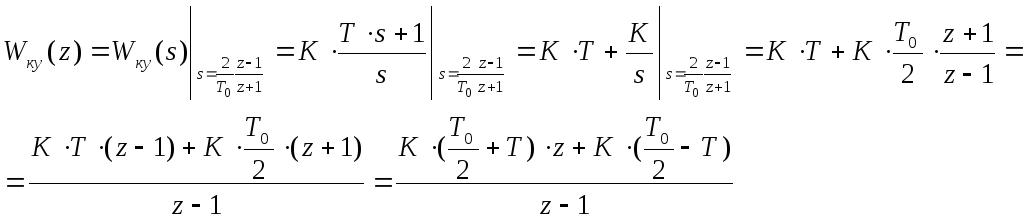
Приравняем передаточную функцию к отношению сигналов на входе и на выходе:

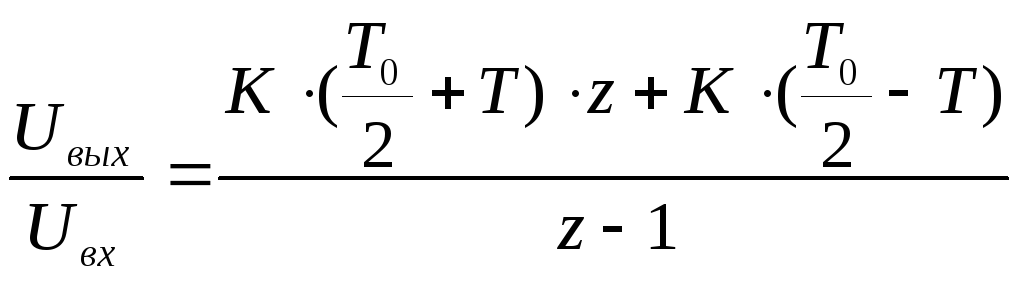
где - сигнал на выходе;

- сигнал на входе.

Выведем формулу необходимую для расчета выходного сигнала цифрового звена.

Где ,

Получаем формулу в которой для расчета выходного сигнала достаточно знать текущее значение сигнала на входе, предыдущее значение входного сигнала и предыдущее значение выходного сигнала. Расчеты по данной формуле реализуем с помощью языка программирования Turbo Pascal

Сравним результаты работы программы Turbo Pascal (приложение) с результатами моделирования в пакете MatLab(Simulink.)

TurboPascalШаг времени – 0,001 с. Диапазон времени моделирования - 0..6 с.

T₀=0,0008 преобразование Тастина

Simulink