3. Получение дифференциальных уравнений отдельных элементов системы и их передаточных функций

3.1 Измерительное устройство

Процессы в измерительном устройстве во временной области можно описать алгебраическим уравнением

Найдём отсюда передаточную функцию электронного усилителя

3.2 Электронный усилитель

Процессы в электронном усилителе во временной области можно описать алгебраическим уравнением

Переходя в Лапласову область и учитывая, что

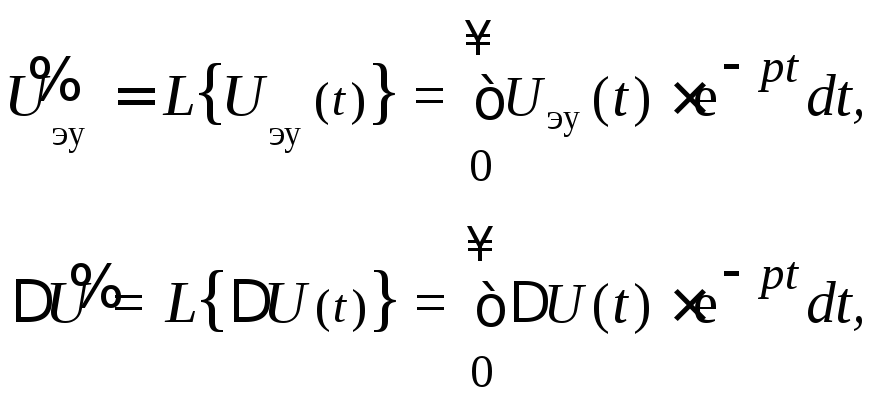
получим

=.

Найдём отсюда передаточную функцию электронного усилителя

3.3 Электромашинный усилитель

Известно, что динамика электромашинного усилителя (ЭМУ) описывается следующим дифференциальным уравнением

,

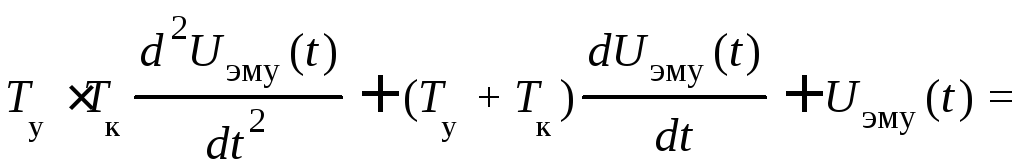
или в изображениях

=.

Это уравнение легко преобразуется к виду

.

тогда передаточная функция

3.4 Двигатель постоянного тока с независимым возбуждением

Из курса ТАУ известно, что дифференциальное уравнение двигателя постоянного тока с независимым возбуждением с углом поворота вала в качестве выходной величины, записывается следующим образом

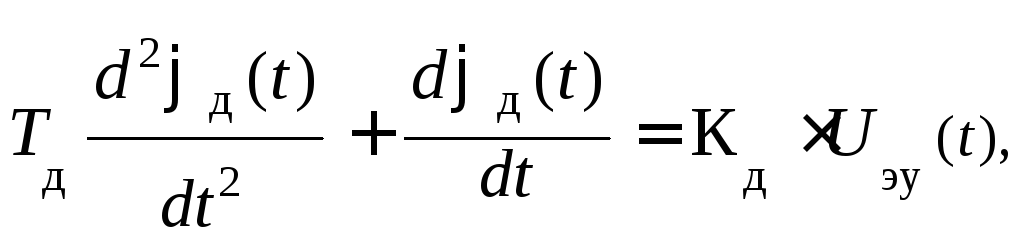
где - угол поворота выходного вала двигателя.

Введя соответствия между оригиналами ,и изображениямиианалогично предыдущему, получим в области Лапласа

,

и, следовательно,

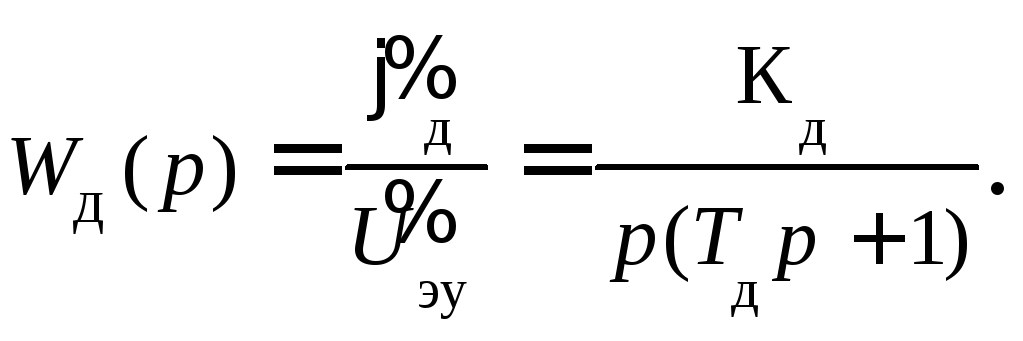
3.5 Редуктор

В следящей системе с ЭМУ редуктор задан своим передаточным числом I_ред . Соответствующее математическое описание редуктора будет иметь вид

Теперь подставим в найденные выражения для дифференциальных уравнений и передаточных функций элементов числовые значения параметров, заданных для данного варианта в таблице 1.

Измерительное устройство

Электронный усилитель

В задании на курсовое проектирование коэффициент передачи электронного усилителя не указан, его нам ещё предстоит определить, поэтому уравнение и передаточная функция ЭУ пока остаются в буквенном виде.

Электромашинный усилитель

.

Двигатель постоянного тока

Редуктор

Теперь, зная математическое описание отдельных элементов САР, можно получить структурную схему системы. Для этого в функциональной схеме (рис.3) в каждом прямоугольнике вместо обозначения функционального элемента (ЭУ, Д, ЭМУ и т.д.) надо записать его передаточную функцию либо дифференциальное уравнение.

4. Получение передаточной функции и дифференциального уравнения разомкнутой исходной системы

Передаточная функция разомкнутой системы определяется как произведение передаточных функций всех звеньев системы

Отсюда получим дифференциальное уравнение разомкнутой исходной системы

5. Определение общего коэффициента усиления (добротности) системы

Добротность системы К может быть определена из выражения

В правой части дифференциального уравнения разомкнутой исходной системы сомножитель и есть добротность системы, поэтому

Отсюда

6. Получение передаточной функции замкнутой исходной системы

С учётом полученного значения =1137.23 передаточная функция исходной разомкнутой системы примет вид

Отсюда видно, что поскольку в знаменателе имеется сомножительр, то рассматриваемая исходная САР – астатическая с первым порядком астатизма.

Дифференциальное уравнение исходной разомкнутой системы при = 1137.23 будет выглядеть так

Передаточная функция исходной замкнутой системы в случае отрицательной единичной обратной связи определится из выражения

В нашем случае

Значит, дифференциальное уравнение исходной замкнутой системы будет