1 Синтез линейной системы

1.1 Получение линеаризованной модели

Объект описывается нелинейным уравнением

(1.1)

Пусть заданному режиму соответствуют

m=;h=;=;=. (1.2)

Обозначим отклонения реальных значений m, h, ,от требуемых через Δm, Δh, Δи Δ, то есть Δm=m-, Δh=h-, Δ=-, Δ=-. Тогдаm=+ Δm; h=+ Δh; =+ Δ;=+Δ. Подставим эти выражения в (1.1) и, рассматриваяF как функцию от независимых переменных m, ,h, ,,,,, разложим ее в ряд Тейлора в точке (1.2) и отбросим малые члены более высокого порядка, чем отклонения. Тогда (1.1) примет вид

+∙Δh+∙Δ+∙Δ+∙Δm=0. (1.3)

Здесь звездочка сверху обозначает, что соответствующие функции и производные вычисляются при значениях аргумента, определяемых соотношениями (1.2). Когда в системе устанавливается заданный режим, уравнение (1.1) принимает вид =0. Вычтя это уравнение из (1.3), получим искомое уравнение звена в отклонениях:

*Δh+*Δ+*Δ+*Δm=0, (1.4)

где

=;

=;

=;

== 0.15

- значения частных производных в точке линеаризации:

=0,02;=0,05;= 0;

Поделив обе части уравнения (1.4) на и оставив в левой части только Δ, получим:

Δ= -20 Δh -196 Δm+3.1 Δ. (1.5)

1.2 Запись модели в форме структурной схемы, передаточной функции и уравнений состояния

Построим структурную схему системы (рис. 3): (здесь и далее все отклонения от величин обозначаются как сами эти величины)

U

U_ЭМ

iэм

Рис. 3 Структурная схема исходной системы

Передаточная функция по управлению имеет вид

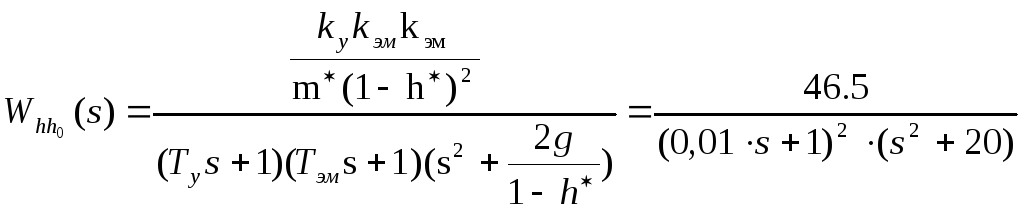. (1.6)

Передаточная функция по возмущению (массе m):

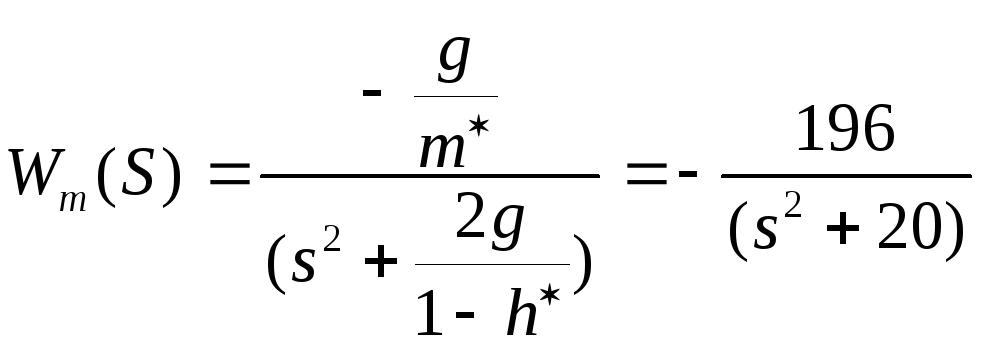. (1.7)

Для получения модели в форме уравнений состояния введем переменные состояния, приняв за них выходы интеграторов (рис. 4).

u

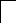
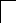
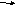
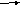
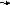
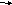
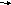
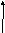
Рис.4 Структурная схема для составления уравнений состояния

Используя структурную схему (рис.4), запишем уравнения состояния:

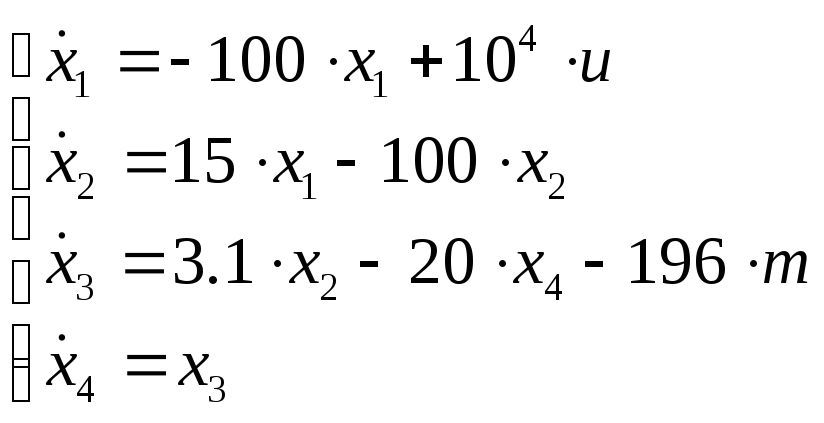(1.8)

Систему уравнений (1.8) запишем в матричном виде:

, (1.9)

где

1.3 Синтез системы стабилизации положения ферромагнитного тела

Смоделируем полученную линейную систему при помощи пакета Classic. Корневая плоскость и переходный процесс в системе изображены на рисунках 5 и 6 соответственно.

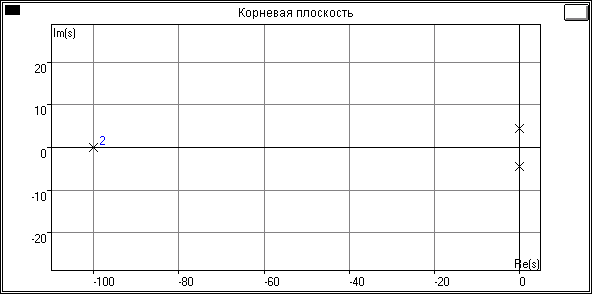
Рис.5 Корневая плоскость исходной модели

Корни характеристического уравнения исходной системы:

p_1,2 = -100; p₃ =4.472j; p₄ = -4.472j.

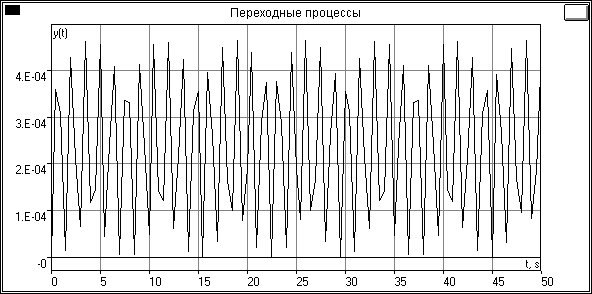
Рис.6 Переходный процесс в исходной системе

Корни p₃ и p₄ находятся на мнимой оси, т.е. система находится на границе устойчивости (процесс колебательный).

Для обеспечения заданного качества переходного процесса в системе используем процедуру модального синтеза. В данной системе необходимо перенести полюсы в левую полуплоскость, учитывая требования к качеству переходного процесса.

Время переходного процесса t_п и перерегулирование σ,% связаны со степенью устойчивости η и колебательностью μ следующими соотношениями[1]:

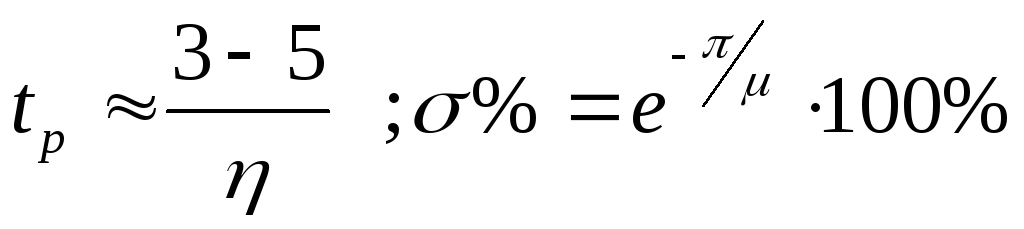, (1.10)

где ,

α и β – вещественная и мнимая части корня, при котором их отношения

максимальны.

Поскольку система колебательная, то ближайшие корни к мнимой оси должны быть комплексно - сопряженные. Из соотношения (1.10) ближайший корень (вещественная часть) α должен иметь величину < -(300 -500), а β → ± (420 -700).

С помощью пакета Classic выбираем желаемое расположение корней, моделируя исходную передаточную функцию и меняя параметры системы, подбираем корни, которые отвечают указанным требованиям:

p_1,2 = -2700; p₃ = -350+480j; p₄ = -350 -480j.

Характеристическое уравнение желаемой передаточной функции имеет вид:

. (1.11)

Время переходного процесса t_p= 0.0096 с и перерегулирование σ = 9.53 %, что удовлетворяет заданным условиям. Комплексная плоскость и переходный процесс желаемой системы представлены на рисунках 7 и 8 соответственно.

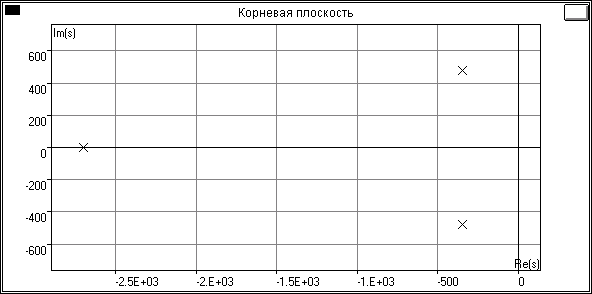
Рис.7 Корневая плоскость желаемой передаточной функции

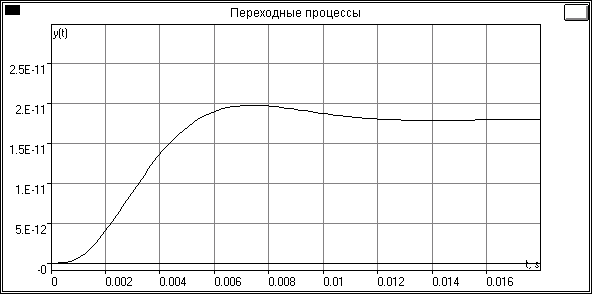
Рис.8 Переходный процесс в желаемой системы (tп=0.0096с.;σ=9.53%)

Для того чтобы сдвинуть полюса нашей системы в точки p₁ – p₄ , необходимо на вход системы завести обратные связи от всех четырех состояний системы как показано на рисунке 9.

Определим матрицу коэффициентов (К) из следующего матричного уравнения:

(1.12)

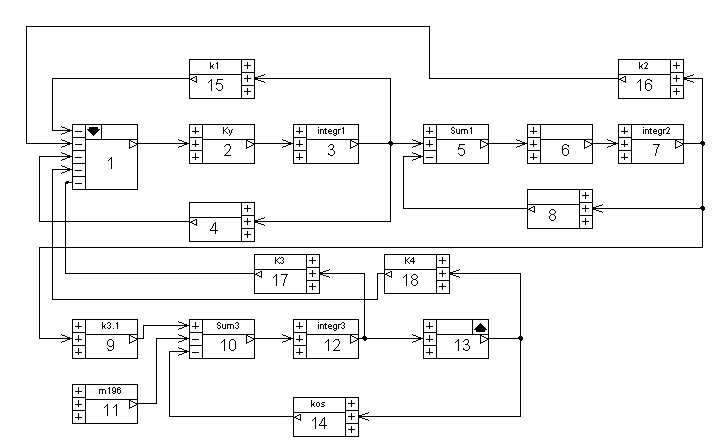
Рис.9 Модель замкнутой САР.

где

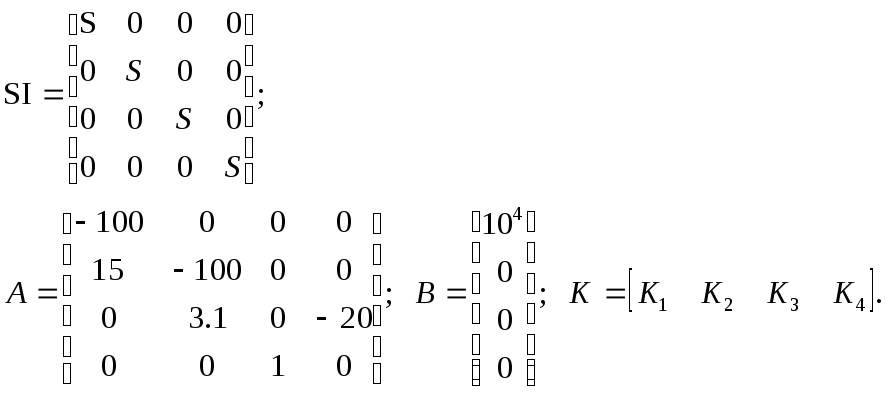
Тогда