ВСТУП

Для реалізації стенда для дослідження структурно-нестабільних механічних систем використаємо як приклад – обернений маятник. Надалі розглядатимемо питання дослідження та стабілізації структурно-нестабільної системи в основі якої лежить обернений маятник.

У теорії управління існує ряд класичних об'єктів, на яких перевіряють як відомі методи розрахунку регуляторів, так і ті що розробляються. До таких об'єктів відносяться коливальні системи, окремим випадком яких є маятникові установки.

В даний час значно розширився клас реальних об'єктів управління, що мають аналогічну математичну модель (наприклад, ракета при злеті, сонячні батареї супутників, управління швидкістю реакції в ядерному реакторі). Це робить актуальним завдання стабілізації маятникових установок.

Питанням стабілізації перевернутого математичного маятника присвячено багато досліджень . У ряді робіт синтез дії, що управляє, виконаний по лінеаризованій моделі об'єкту і отриманий лінійний по координатах стану алгоритм управління, що дозволяє забезпечити стійкість системи при малих кутах відхилення від положення рівноваги . Застосування кусочно-лінійної апроксимації нелінійного маятника і методів оптимального управління дає рішення задачі для великих початкових збурень. В цьому випадку потрібний великий об'єм обчислень, крім того, складно одночасно забезпечити стійкість рішення і надійність системи. Розглянуто завдання розгойдування і стабілізації маятника у верхньому положенні з одночасною стабілізацією рухомої платформи, на якій закріплена вісь маятника. Отримані релейні закони управління на основі диференціальної і кінцевої форм алгоритму швидкісного градієнта. У багатьох роботах завдання управління однозвенним маятником вирішується шляхом переміщення точки підвісу маятника, як в маятнику Капіци.

І. ОСОБЛИВОСТІ ПОВОДЖЕННЯ ДИНАМІЧНИХ СИСТЕМ

Р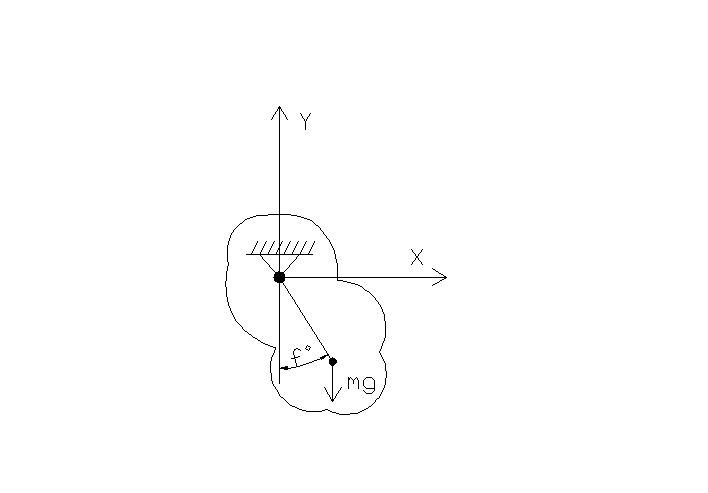озглянемо основні особливості поводження динамічних систем на прикладі систем з одним ступенем вільності. Як відомо, кількість ступенів вільності дорівнює кількості координат, необхідних і дос­татніх для однозначного опису положення системи в просторі. Так, абсолютно тверде тіло, яке може коливатися під дією сил тяжіння нав­колонерухомої горизонтальної осі, має один ступінь вільності, ос­кільки для визначення положення тіла досить знати один параметр - кут його відхилення від вертикалі /рис 1/.

Схема фізичного маятника

1. Вільні коливання

Розглянемо математичний маятник, який здійснює коливання у вертикальній площині навколо точки 0 /рис. 1/. При відхиленні маятника на кут φ від вертикалі на нього як на матеріальну точку масою т у напрямку дотичної до траєкторії центру мас С діє відновлювальна сила, яка залежить від узагальненої координати φ /рис. 2/:

1.1

С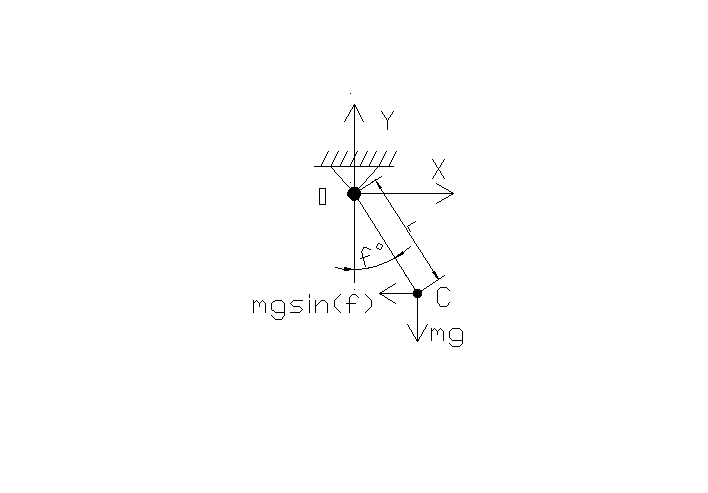хема математичного маятника

Очевидно, ця сила відноситься до позиційних. Дуга, яку опи­сує в своєму русі матеріальна точка, має довжину , дотичне прискорення точки дорівнює а дотичні сила інерції

. 1.1

Підстави вам значення цих сил у рівняння Д’аламбера, одержимо рівняння:

, 1.2

або позначаючи

, 1.3

перетворимо його до вигляду

. 1.4

Рівняння виявляється нелінійним через те що другий доданок /1.4/ залежить від невідомої координати нелінійно.

Оскільки крім тяжіння на маятник не діють ніякі інші зовнішні навантаження, рівняння /1.4/ описує вільні, або власні, вливання маятника.

Якщо розглядати лише малі кути відпилення маятника від вертикалі, тобто <<1 радіану, то вираз /1.4/ можна спростити. Для цього є розкладі функції sin у ряд за степенями :

необхідно залишити тільки перший член (інші члени за цієї умови утворюватимуть набагато менший доданок).

Рівняння /1.4/ за цієї умови перетворюється у лінійне рівняння:

1.5

в якому величина визначає власну частоту малих коливань маятника.

Рівняння /1.5/ - найпростіше лінійне рівняння системи з од­ним ступенем вільності - лінійного осцилятора.

Покажемо, що до рівняння /1.5/ зводяться рівняння руху багатьох інших нелінійних /у загальному випадку/ систем.

Розглянемо, наприклад, рух матеріальної точки на горизонтальній площині, зв’язаної двома пружинами а з жорсткістю С/2 з двома нерухомими точками і/рис. 3/. Рівняння руху вздовж осі цієї системи одержимо з умови рівноваги сил що прикладені до маси т.Обидві пружини при знаходженні иси т у точці рівноваги 0 попередньо натягнуті. Силу цього попереднього натягу позчимо . При відхиленні маси т /точки С / від положення рівноваги О на величину y довжина пружини дорівнюватиме .

При цьому сила натягу пружини, пружини, спрямована вздовж осі пружини /линії 0. С лівої пружини/, зросте на величину

1.6

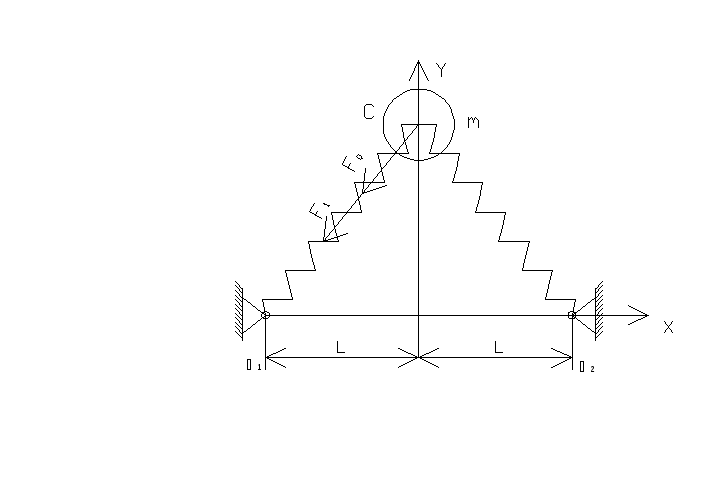
Рис. 3. Схема коливальної системи

До неї слід додати сулу попереднього натягу , яка зараз також буде спрямована вздовж осі пружини.

Таким чином, з боку однієї пружини на масу т у напрямку осі у діятиме відновлююча сила:

1.7

Така сама сила діятиме з боку іншої пружини. В іцлому

1.8

Додаючи до /1.8/ силу інерції , одержеємо

1.9

Як видно, це рівняння також виявилося нелінійним, його можна спростити, якщо обмежитися тільки малими відхиленнями маси т , тобто припустити, що у < L. При цьому приблизний вираа /1.8/ набуває вигляду:

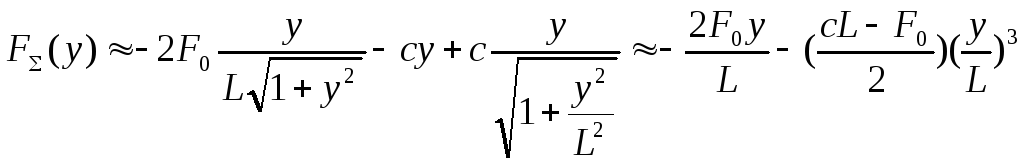1.10

Тут використана приблизна рівність:

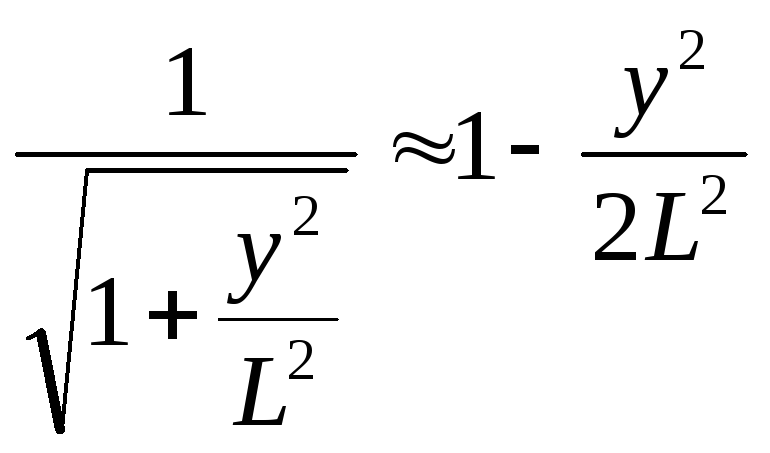1.11

Що справедлива при малому значенні y/L, яке припускалося раніше.

3 точки зору одержання рішення рівняння /1.9/ степенева нелінійність значно простіша початкової трансцендентної нелінійності /1.8/.

Далі, при великому попередньому натягу пружин і малих відхиленнях у у виразі /1.10/ можна знехтувати другим членом. І Тоді рівняння /1.9/ стає лінійним і приймиає вигляд рівняння /1.4/:

,. 1.12

Зауважимо, що при відсутності попереднього натягу пружин навіть при малих відхиленнях точкиО від положення рівноваги неможливо користуватися наближеними лінійними виразами. Відновлююча сила в околі положення рівноваги буде при цьому пропорційна третьому ступеню відхилення у /1.12/. Лінійне диференціальне рівняння /1.12/ з нелінійним коефіцієнтом має рішення, яке можна подати в двох формах:

1.13

де ;.

Довільні сталі ,(абоа, φ) можна знайти з початкових умов.

Якщо при t=0 на початку руху у(0)=;то при підстановці цих умов у (1.13) і випливаючого з нього

знайдемо

1.14

Тайм чином, при вільних /власних/ коливаннях рух маси описується синусоїдальшм законом іа частотою , амплітудою а і початковою фазою φ, Можна стверджувати, що будь-яка система, рух якої описується рівняннями /1.5/ чи /1.12/, коливається згідно, із законом /1.13/ з параметрами /2.14/, власною частотою і періодом

. При цьому коливвння системи є стаціонарними, періодичними і мають гладку /без зламів/ форму залежності від ча­су. Такі коливання називають гармонійними.

ІІри складанні рівнянь /1.5/ і /1.12/ припускалася відсутність якого-небудь опору руху маси т. Наявність такого опору призводить до розсіювання (дисипації) енергії коливальної системи і назива­ється демпфіруванням коливань.

Залежність сил опору від швидкості руху коливальної системи в кожному конкретному випадку визначається фізичною природою коли­вального процесу, що розглядається, найбільш простою й поширеною моделлю тертя є в"язке тертя, при якому сила опору припускається пропорційною швидкості руху: . В"язке тертя виникає наприклад, у гідравлічних амортизаторах, які працюють при ламінарному режимі течії рідини; внутрішнє тертя у матеріалі елемента, що деформується, також іноді моделюється в"язким тертям.

При наявності в"язяого тертя у системі рівняння /1.12/ записуеться у вигляді

1.15

де .

Згідно з правилом знаходження загального рішення однорідних лінійних диференціальних рівнянь з незмінними коефіцієнтами рішен­ня рівняння /1.15/ запишемо у вигляді і підставимойого в /1.15/. Унаслідок цього одержимо характеристичне рівняння

1.16

звідки при

тобтобто корені ікомплексно спряжені.

У цьому разі загальне рішення y(t) буде визначатися формулою

,

або

1.17

де , а амплітуда і фаза обчислюється згідно з /1.13/.

Позначивши зміщення і швидкість системи /1.15/ у початкову мить t=0 відповіноі, знайдемо;звідки випливає що;.

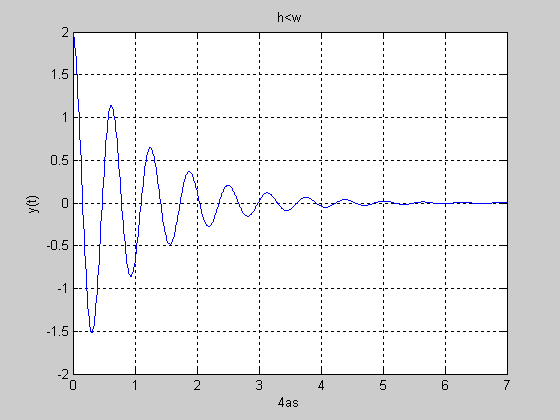
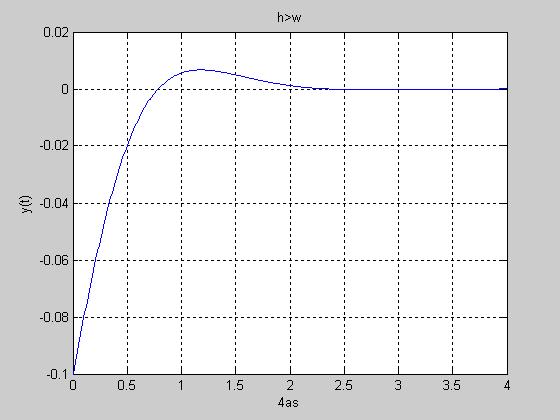Таким чином, принаявності в"язкого опору рух системи описуеться неперіодичним законои /1.17/, який для наведено графічно на рис.4.

Рис. 4.

Період згасаючих коливань, який визначається часом між двома максимальними зміщеннями маси,

.

У випадку великого опору / /обидва корені характеристичного рівняння /1.16/ дійсні й від’ємні:

.

Загальний інтеграл рівняння /1.15/ набувае вигляду

. 2.18

З початкових умов знайдемо сталі:

; ;

де .

2. Вимушені коливання

При вимушених коливаннях до рівняння руху /1.12/ або /1.15/ входить залежний тільки від часу член f(t). Тому рівняння ру­ху набуває вигляду:

2.1

Значний практичний інтерес викликають періодичні збурюючі функції, які в багатьох випадках можна зобразити за допомогою гармонічного закону

де відповідноамплітуда і частота збурення.

Розглянемо різні типи збурення для одномасової моделі /1.5/, яка складається з маси т пружини та демпферу.

У першому випадку /рис.5,а/ збурення системи здійснюється за рахунок періодичного руху точки підвісу пружини. Видовжувіння пружини виражається різницею тому рівнянняруну матиме вид

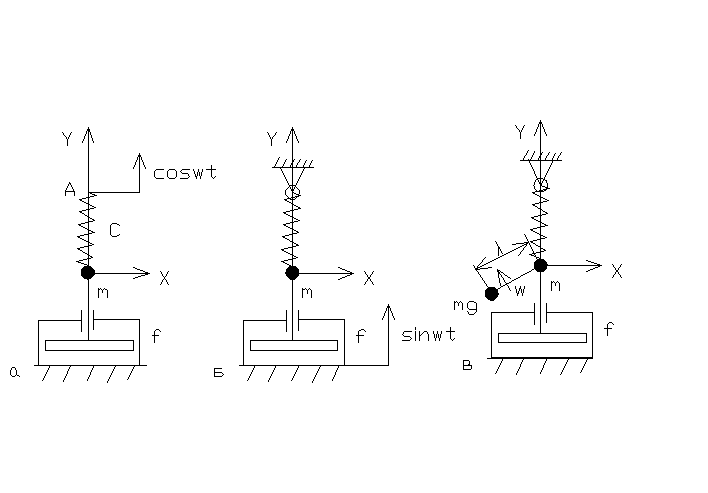
Рис. 5. Варіанти збурення механічної системі: а - кінематичне

через пружини; б - кінематичне через демпфер: в - інерційне через ексцентрик

Приводячи це рівняння до стандартного вигляду, одержуемо

2.2

Для осцилятора, схема якого зображена на рис.5,б, сили демпфірування пропорційні швидкості переміщення маси корпусу демпфера, який здійснює коливання згідно з законом .

У цьому разі рівняння руху має вигляд

або

2.3

У випадку збурення осцилятора через ексцентрик, який обертається /рис.5,б/, виникає сила інерції врахування якої при рівномірному обертанні ексцентрику призводить до рівняння руху

Для загальної маси осцилятора рівняння руху набуває вигляду

2.4

Причому тут

Очевидно, рівняння /2.2/-/2.4/ відрізняються лише коефіці­єнтом при функції косинуса. Отже, у загальному випадку можна записати

2.5

де вираз р у кожному з трьох випадків має відповідно такий вигляд:

а) б)в)2.6

Оскільки коефіцієнти р не залежать від часу, то рішення для ножного з трьох розглянутих виразів зовнішнього збурення можна шукати з рівняння /2.5/.Знайдемо часткове ріщення цього рівняння, яке описує стаціо­нарний періодичний рух із періодом збурюючої сили (рух, що залежить від початкових умов, з часом затухає й найчастіше не становить практичного інтересу).

Шукане часткове рішення запишено у вигляді

2.7

Підставивши /2.6/ у /2.4/ і приводячи подібні члени, одержимо

Це співвідношення є слушним у будь-яку мить лише тоді, коли вирази у квадратних дужках водночас дорівнюватимуть нулю. З цієї умови визначаються:

2.8

Фізично вираз /2.7/ означає, до гармонічні коливання здійснються з амплітудою і відстають за фазою відносно збурюючої дії на кут φ. При цьому є мірою величини збурення,а а коефіцієнт динамічності, який показує, у скільки разів амплітуда коливання більша за амплітуду збурюючого навантаження . Графіки залежності амплітуди а і зсуву фаз від частоти збурюючої дії називаються відповідно амплітудними (АЧХ) і фазовими /ФЧХ/ частотними характеристиками і дають можливість судити про найважливіші властивості систем, що здійснюють вимушені коливання.

Із співвідношення /2.8/ випливає, що зсув фаз φ не залежить від р тому ФЧХ однакова для всіх трьох випадків зовнішнього збурення. Зауважимо, що у другому випадку кут φ має зміст фазово­го куту між відхиленням у та швидкістю зсуву корпуса демпфера. На рис.6 зображено фазову частотну характеристику для різних значень демпфірування. При цьому використані більш зручні відносні позначення:

2.9 відносне значення частоти зовнішньої дії (відношення цієї частотм до частоти власних коливань системи);

2.10

відносний коефіцієтн згасання.

Рис.6

Співвідношення /2.8/ набуває вигляду

2.11

Коефіціенти динамічності визначаються з /2.8/ з урахуванням /2.10/ і /2.11/:

а) ;

б) 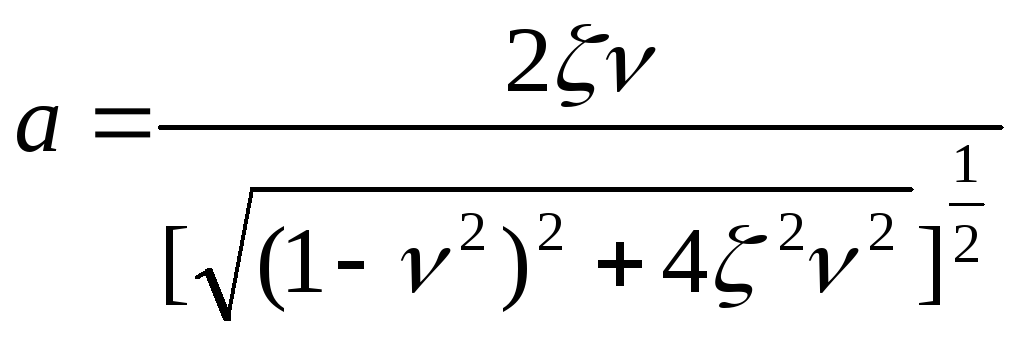; 2.12

в) .

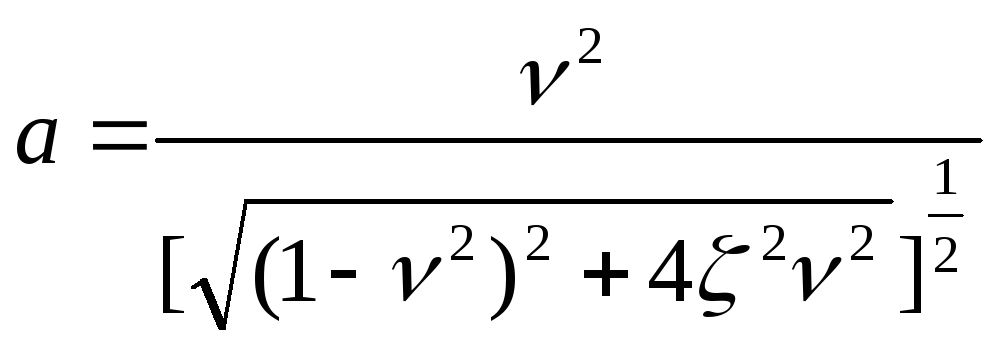3. Коливання оберненого маятника.

Далі розглянемо параметри динамічних систем фізичною основою яких є обернений маятник, стабілізація верхнього положення якого досягається різними методами.

Впраці Т.Г. Стрижак під назвою «Методи дослідження динамічних систем типу маятник» приводиться кілька способів стабілізації верхнього положення оберненого маятника.

Зокрема такі:

а) коливання точки підвісу по вертикалі

Рівняння руху маятника матиме вигляд:

,

де періодична чи квазіперіодична функція за якою рухається точка підвісу.

Тоді умова стійкості матиме вигляд

де а ω амплітуда і частота збурюючої сили відповідно

б) коливання точки підвісу по еліпсу

Рівняння руху маятника матиме вигляд:

Тоді умова стійкості матиме вигляд

в) коливання точки підвісу по петлі витягнутій в вертикальному положенні

Рівняння руху маятника матиме вигляд:

Тоді умова стійкості матиме вигляд

II. СТАБІЛІЗАЦІЯ ОБЕРНЕНОГО МАЯТНИКА СИСТЕМОЮ З СИГНАЛЬНОЮ НАСТРОЙКОЮ.

Синтез адаптивної системи виконаний на основі методів еталонного рівняння, вектора швидкості, другого методу Ляпунова. Приведені результати пасивного експерименту, рекомендації по вибору параметрів системи.

Згідно вибраному методу в системі організовуються різнотемпові рухи - так, щоб неконтрольовані збурення локалізувалися в контурі швидких рухів, а властивості контура повільних рухів задовольняли бажаним динамічним вимогам. Такий ефект досягається за допомогою зворотного зв'язку по вектору перших похідних координат стану або по похідним вихідний змінної.

Структура регулятора отримана методом еталонного рівняння. Нелінійний об'єкт представлений у вигляді двох підсистем - «маятник» і «платформа». Бажані динамічні властивості системи задаються еталонним диференціальним рівнянням, коефіцієнти якого розраховані за вибраними показниками якості. Для стабілізації маятника у верхньому положенні і рухомої платформи пропонується використовувати алгоритм управління з сигнальною настройкою, який також можна віднести до виду астатичних законів управління із старшою похідною вихідний змінної. Використання інформації про кутове прискорення дозволяє підвищити швидкість відгуку регулятора на зміну стану системи.

Для оцінки необхідних похідних використовуються два малоінерційні лінійні фільтри першого і другого порядку. Присутність в системі малоінерційних фільтрів оцінки похідних і «швидкого» адаптера, що реалізовує сигнальну настройку, приводять до виникнення різнотемпових процесів. Одній з проблем, що виникають при розрахунку параметрів системи, є визначення постійних часу фільтрів оцінки похідних і еталонних моделей підсистем, коефіцієнта передачі адаптера. Ці величини зв'язані між собою і, крім того, залежать від кута відхилення маятника, що виникає через дію зовнішніх сил.

Постановка задачі

Модель системи маятник-платформа

Розглядається модель перевернутого маятника, вісь якого закріплена на рухомій платфомі. Переміщення платформи характеризуеться функцією s(t), а кутове відхилення маятника – функцією φ(t). Маса маятника дуже мала порівняно з масою платформи . На маятникдіє сила прикладена в центі мас маятника.

Математична модель такої системи має вигляд:

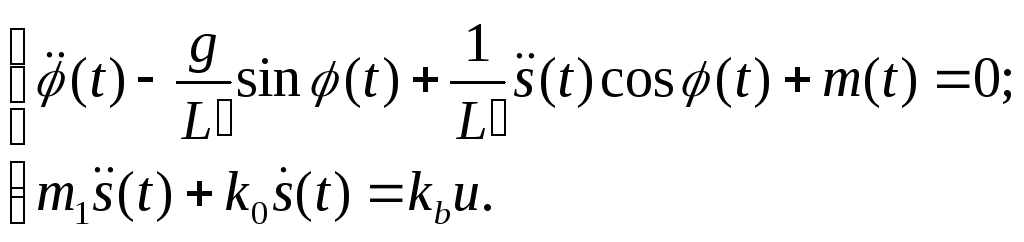3.1

де - ефективна довжина маятника,

J – момент інерції відносно центра мас;

L – відстань між осю та центром мас;

- коефіціент тертя ;

- коефіціент передачі ;

u – управляючий крутячий мометн.

Особбливість моделі полягає в тому що при малих кутах відхилення її динаміка може бути описана лінійними диференційними рівняннями, а при великих кутах – нелінійними. Задаємось обмеженням переміщення платформи:

обмеженням амплітуди та темпа зовнішнього впливу

, ,,,

Припускаємо що тертя осі маятника мале, а такожож що відхилення маятника та переміщення каретки відомі.

Мета функціонування системи полягає в стабілізації маятника у верхньому положенні рівноваги і в стабілізації платформи незалежно від початкових умов в підсистемі «маятник» і обмежених зовнішніх збуреннях, тобто повинні виконуватися умови: Величина кута відхилення маятника від вертикальної осі, яку система зможе «відпрацювати», залежить від ресурсу управління і допустимого пробігу платформи. Надалі вважаємо, що кут відхиленнямаятника не перевищує ±60°.

Опис системи стабілізації з сигнальною настройкою

Нелінійний об'єкт /3.1/ представлений у вигляді двох підсистем другого порядку: «маятник» і «платформа». Перепишемо модель об'єкту, використовуючи позначення вихідних змінних:

. 3.2

Тоді рівняння /3.1/ матимуть вигляд:

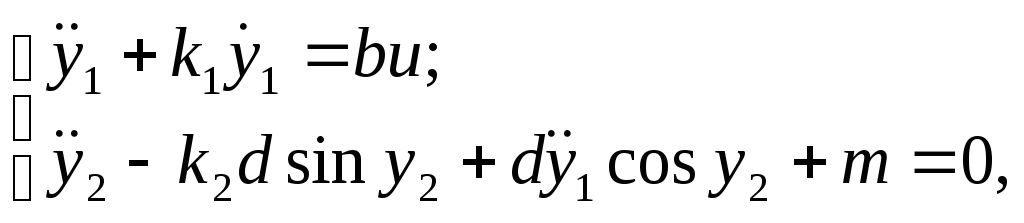3.3

де

Перетворим /3.3/ виключивши з другого рівняння :

3.4

У відповідності до вимог по швидкодії системи задамо еталонні процеси управління системою:

3.5

де - постійні додатні коєфіціенти.

Керуючий сигнал представимо у вигляді суми двох складових:

де івизначимо з рівності правих частей рівнянь /3.4/ та /3.5/.

В результаті закон керування набуде вигляду:

3.6

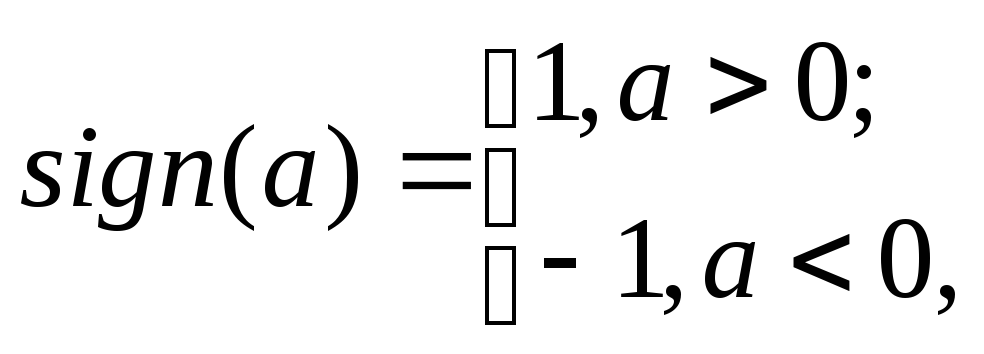де 3.7

- коефіцієнт передачі, значення якого задовольняє умовам <.

Рівняння /3.6/, /3.7/ описують алгоритм управління з сигнальною настройкою, який також можна віднести до виду астатичних законів управління із старшою похідною вихідний змінної.

У системі /3.4/, /3.6/, /3.7/ дія, що управляє, і змінна сигнальної настройки формуються на основі інформації про похідних вихідних змінних Оцінка похідних здійснюється за допомогою лінійних малоінерційних ланок, які прийнято називати диференціюючими фільтрами або фільтрами оцінки похідних (ФОП).

Швидкість руху платформи оцінюється фільтром першого порядку:

3.8

де мала постійна часу;

, оцінкитавідповідно.

Перша і друга похідні від кута відхилення маятника оцінюються інерційною ланкою другого порядку з відповідною постійною часу () і коефіцієнтом демпфування ():

3.9

Враховуючи змінні отримані за допомогою ФОП, рівняння регулятора мпримуть вигляд:

Приклад чисельного моделювання

Моделювання системи стабілізації з сигнальною настройкою виконане при наступних параметрах об'єкту управління: , , , .

Обмеження на переміщення платформи прийняте рівним 5 м. Коефіцієнти еталонних рівнянь /3.5/ визначені на основі показників якості, що характеризують швидкодію системи ()і перерегулювання (%).

В результаті еталонні функції і мають вигляд:

Інерційності ФОП /3.8/, /3.9/ в контурах керування платформи та маятника приймалися рівними: - на порядок менші за мінімальні постійні часу еталонних моделей.

Процеси що відбуваються в системі при відпрацюванні кута відхилення маятника від положення рівноваги в 30 градусів показані на рис. 8.

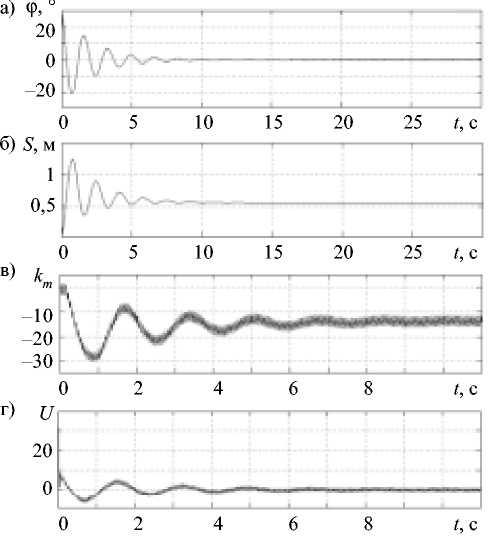
Рис. 8. Графіки процесів в системі стабілізації при відпрацюванні кута 30º

а) зміна кута нахилу; б) переміщення платформи;

в) вихідна змінна адаптера; г) управляючий сигнал

Маятник повертається у вертикальне положення, а платформа зупиняється, але її положення зміщене щодо початкового положення.

Максимальне відхилення платформи від початкового положення і значення її кінцевої координати істотно залежать від кута відхилення маятника (рис. 9,а), який також впливає і на максимальну величину дії, що управляє (рис. 2,б). Властивості системи залежать від співвідношення між постійними часу ФОП (), еталонних моделей () і коефіцієнтом передачі адаптера ().Чим менше інерційність ФОП, тим більше повинен бути коефіцієнт передачі адаптера, чим більше кут, тим ближче по значеннях повинні бути і постійна часу ФОП.

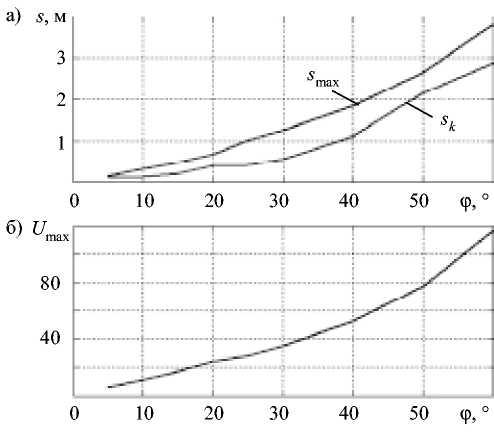
Рис. 9. Вплив кута відхилення маятника на максимальне відхилення і кінцеве положення платформи (а), на максимальне значення керуючого сигналу (б).

Визначено, що платформа може повернутися в початковий стан, якщо =0,025. Одночасна стабілізація маятника і платформи на початку координат при кутах відхилення, що не перевищують ±60°, можлива, якщо відношення між та рівне 0,125.

ІІІ. МОДЕЛЮВАННЯ СИСТЕМИ КЕРКВАННЯ З СИГНАЛЬНОЮ НАСТРОЙКОЮ В СЕРЕДОВИЩІ MATLAB.

Використовуючи методику наведену вище, моделювання системи методами MatLab, не вдається досягнути бажаних результатів. Система керування виявляється нестійкою.

Нижче будуть представлені три моделі що відрізнятимуться методом побудови системи керування та фільтрами оцінювання похідних.

В першому наближенні модель системи підтримує стійке положення оберненого маятника в невеликому діапазоні початкових кутів відхилення з невеликим розходженням коливань.

Модель системи 1

Ефективна довжина маятника - 0.3 м.

Маса маятника – 0.05 кг.

Маса візка – 0.8 кг.

Початковий кут відхилення – 0.2 рад.

Графік зміни кута відхилення від положення рівноваги зображений на рис. 10

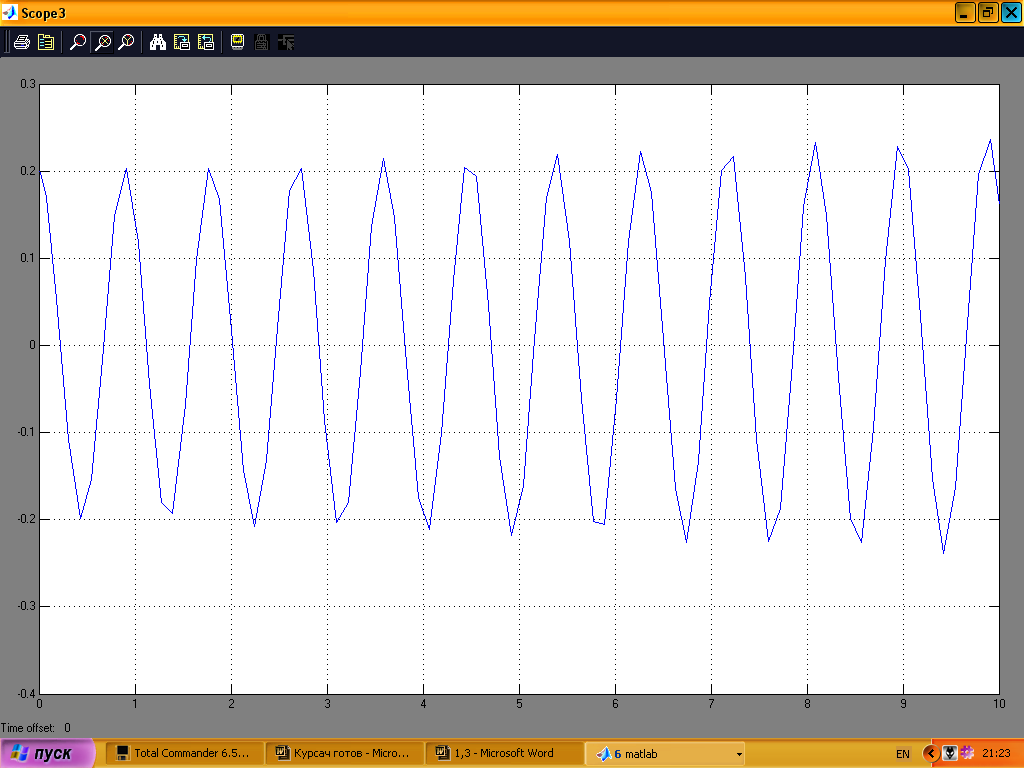
Рис. 10.

Графік переміщення платформи рис. 11

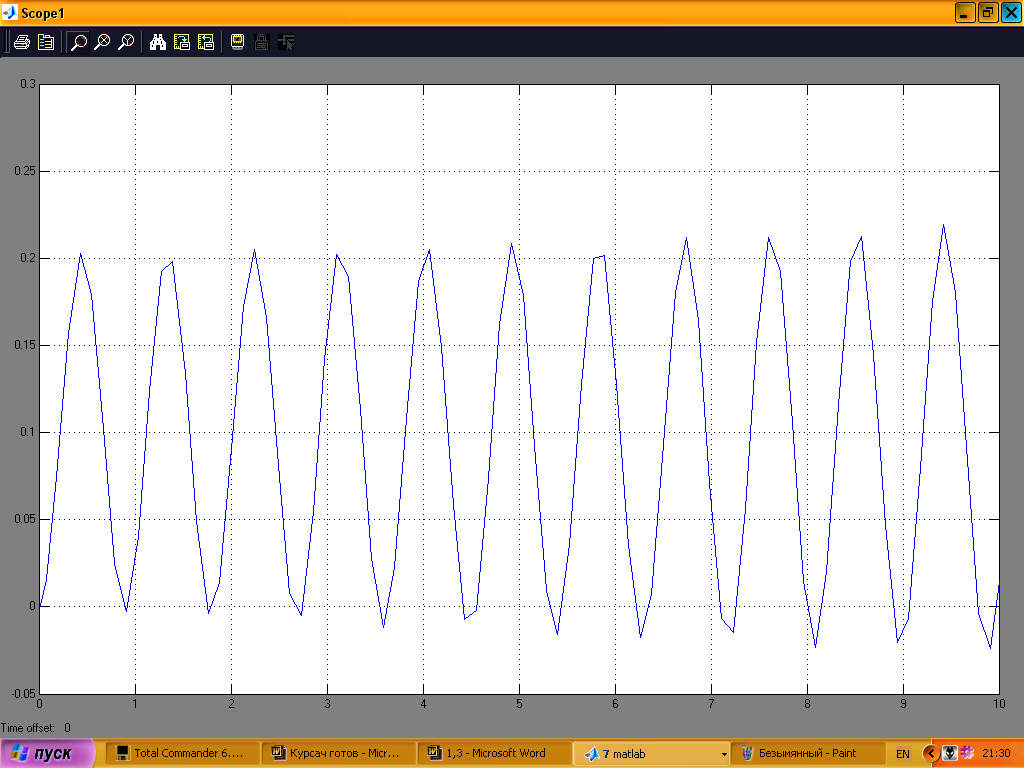
Рис. 11

Як бачимо система нестійка. Методом її стабілізації можна використати введення коефіцієнтна демпфування в підсистемі «маятник». Однак це призводить до постійного дрейфу системи «платформа».

На рис. 12 показана зміна початкового кута нахилу, на рис.13 переміщення платформи. Параметри установки такі ж самі.

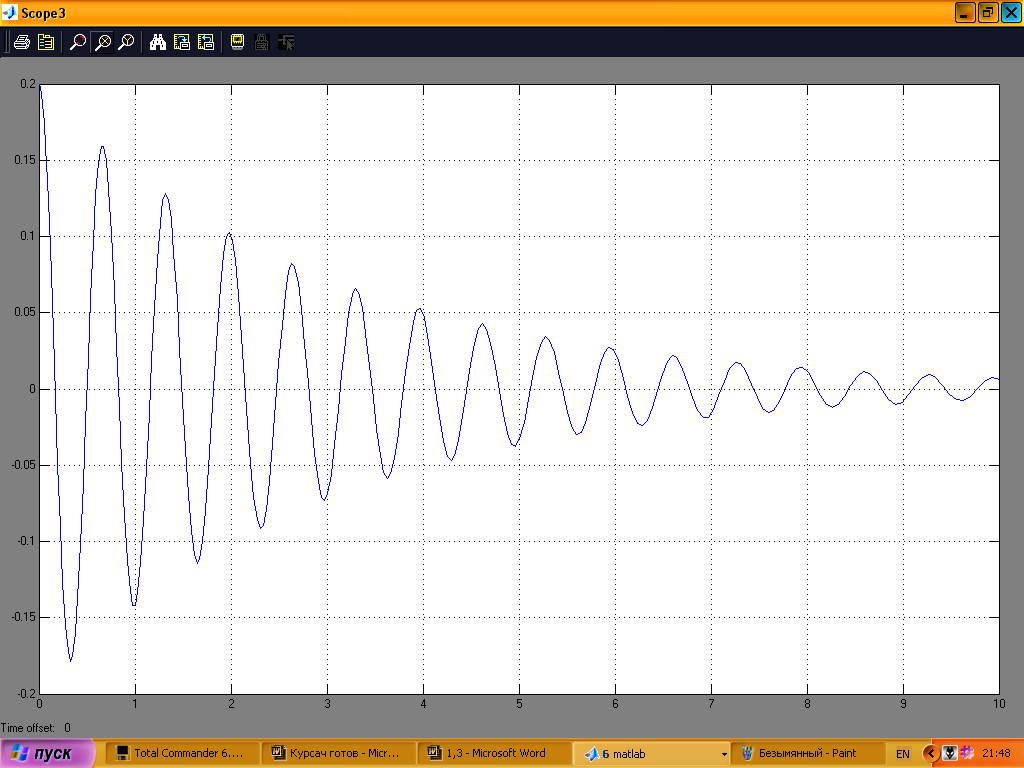
Рис. 12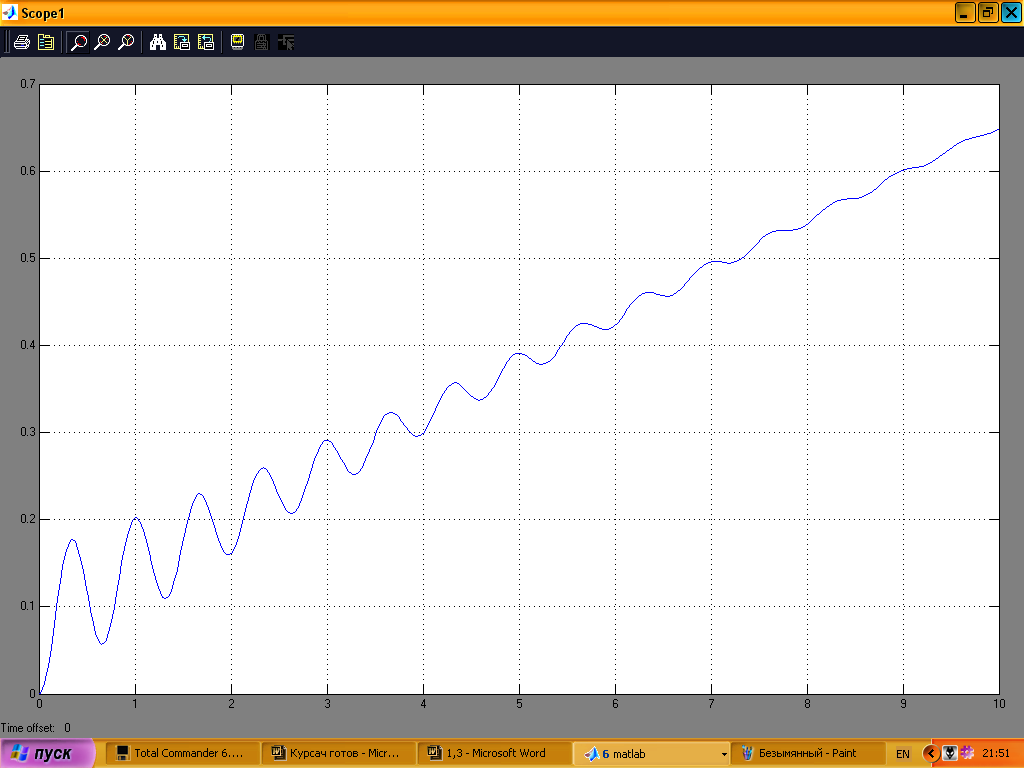

Рис. 13

Зміна коефіцієнтів передачі, параметрів самого об’єкта керування не приносить значних змін. Система залишається нестійкою. Тому наступний крок це ускладнення системи стабілізації еталонними системами та двома фільтрами оцінювання похідних .

В другому наближенні модель системи підтримує стійке положення оберненого маятника в невеликому діапазоні початкових кутів та виявляється стійкою на невеликому проміжку часу. Приблизно 2.3 секунди. Потім з’являється дрейф по куту та відхилення платформи.

Модель системи 2

Ефективна довжина маятника - 0.67 м.

Маса маятника – 0.05 кг.

Маса візка – 0.8 кг.

Початковий кут відхилення – 0.2 рад.

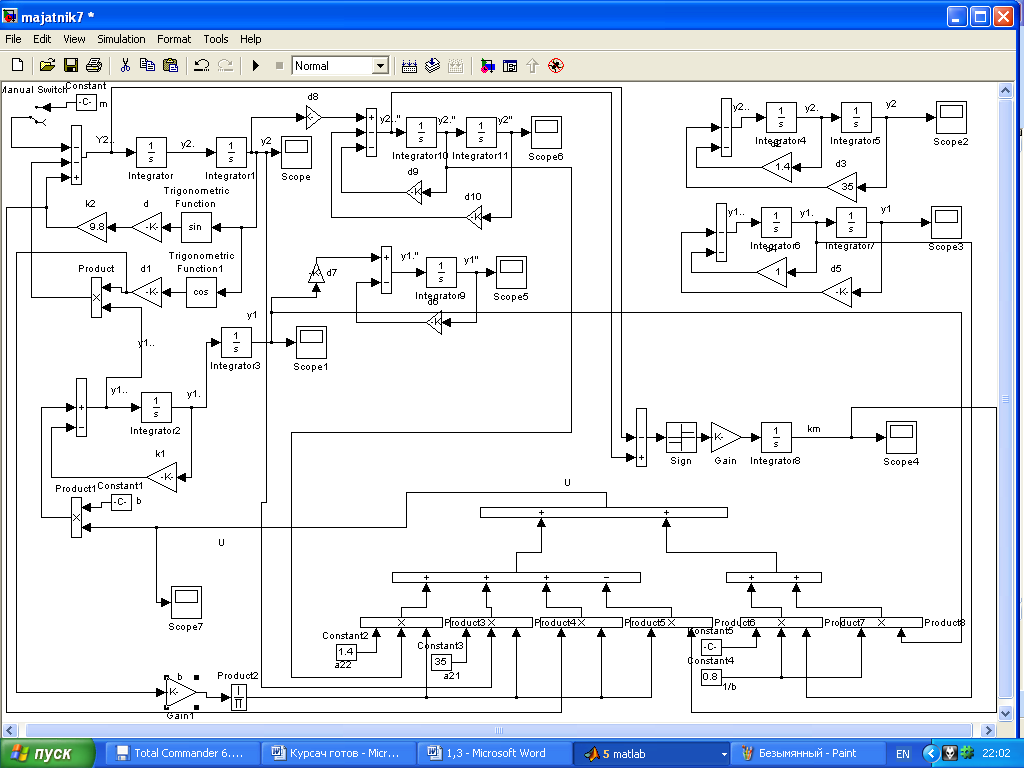
В даній моделі керування параметри всіх складових аналогічні параметрам системи описаній в розділі ІІ наведеному вище.

Однак, як видно з графіків (рис.14, рис.15), керуюча підсистема не відпрацьовує початковий кут відхилення як це описувалось в розділі ІІ.

На рис. 14 показана зміна початкового кута нахилу, на рис.15 переміщення платформи, на рис.16 керуючий сигнал; графіки подані дня проміжку часу 0–2с.

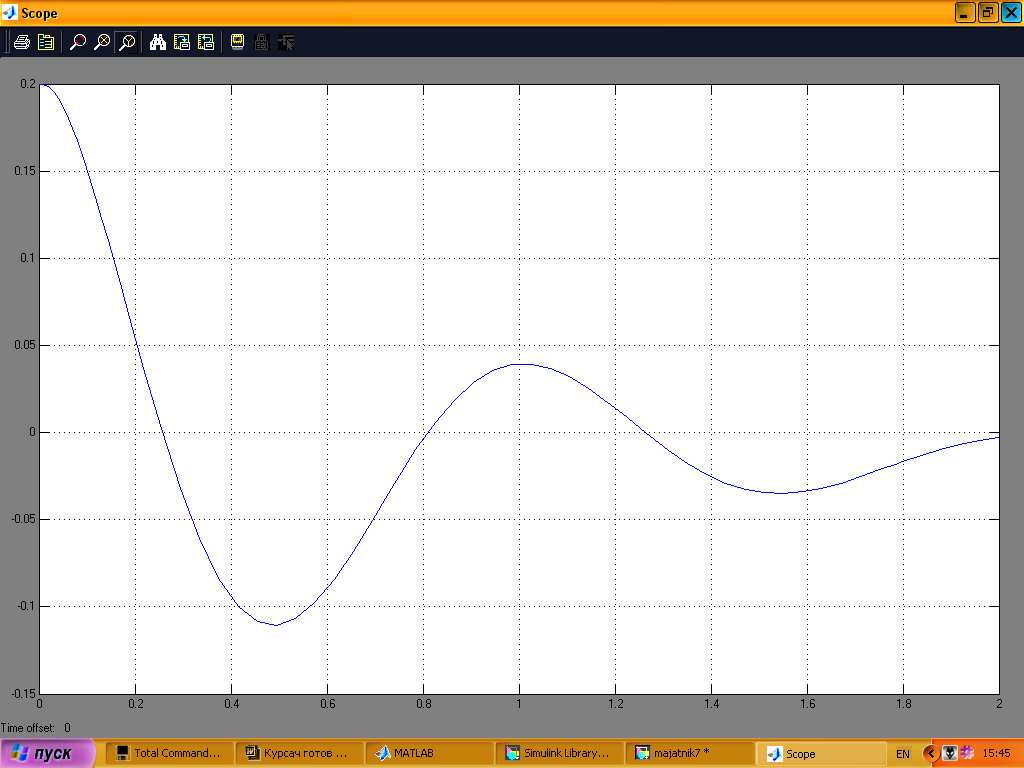
Рис. 14

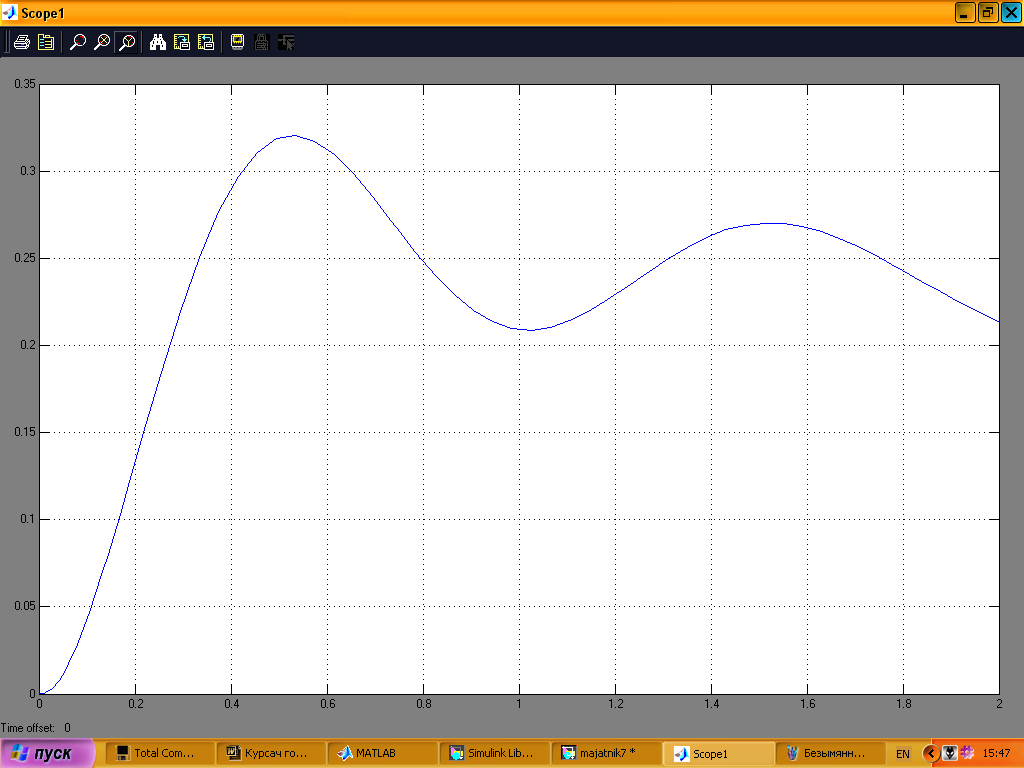
Рис. 15

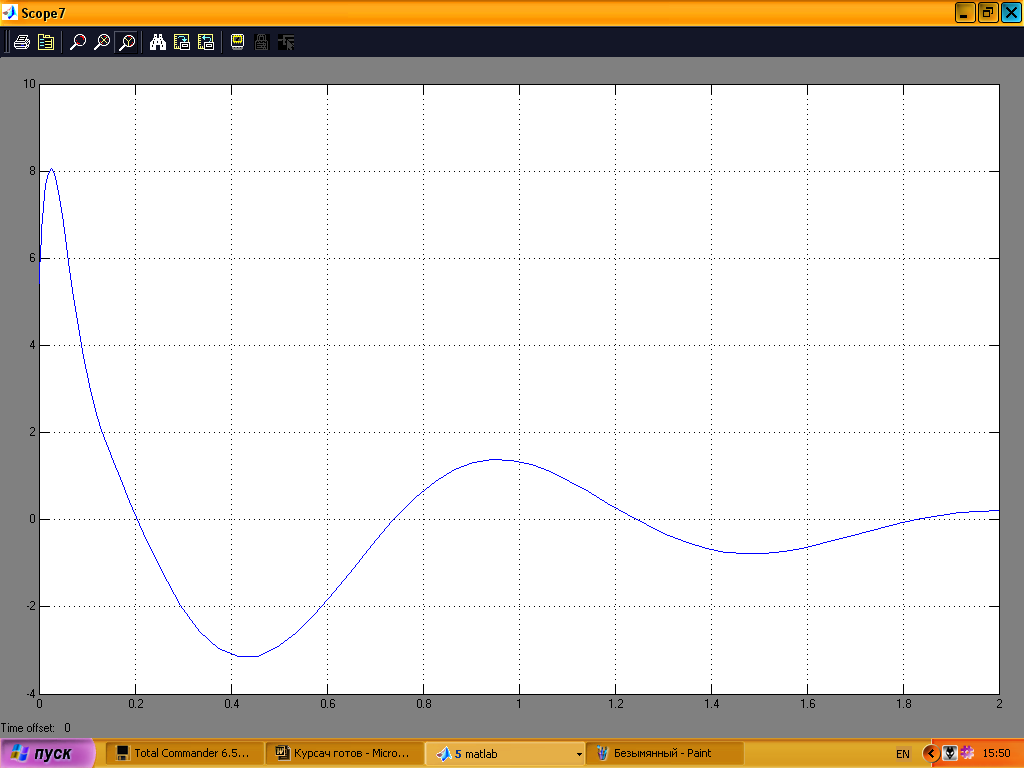
Рис. 16

Система втрачає стійкість після 2-ї секунди роботи.

На рис.17 показана зміна початкового кута нахилу, на рис.18 переміщення платформи, на рис.19 керуючий сигнал; графіки подані дня проміжку часу 0–30с.

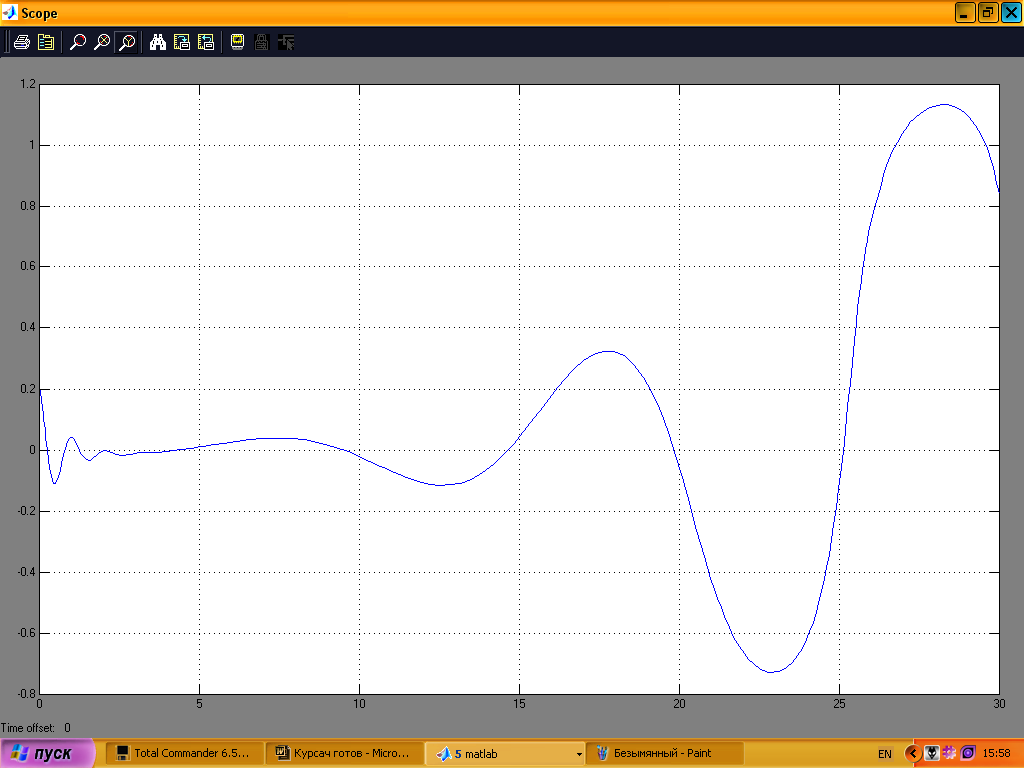
Рис. 17

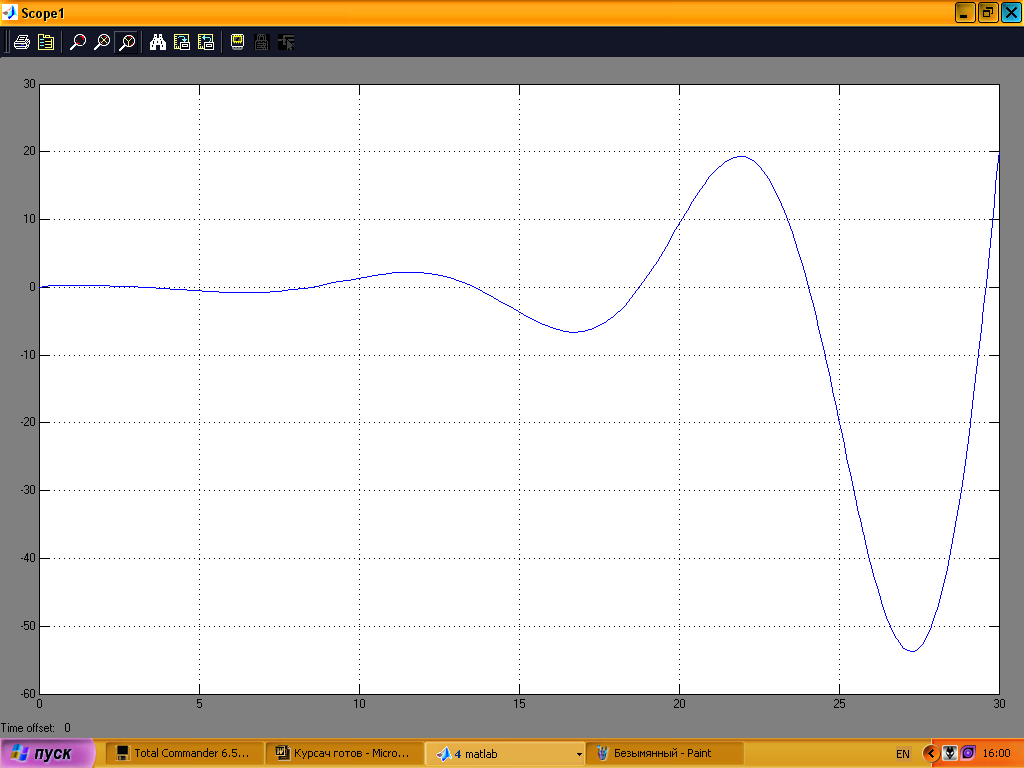
Рис. 18

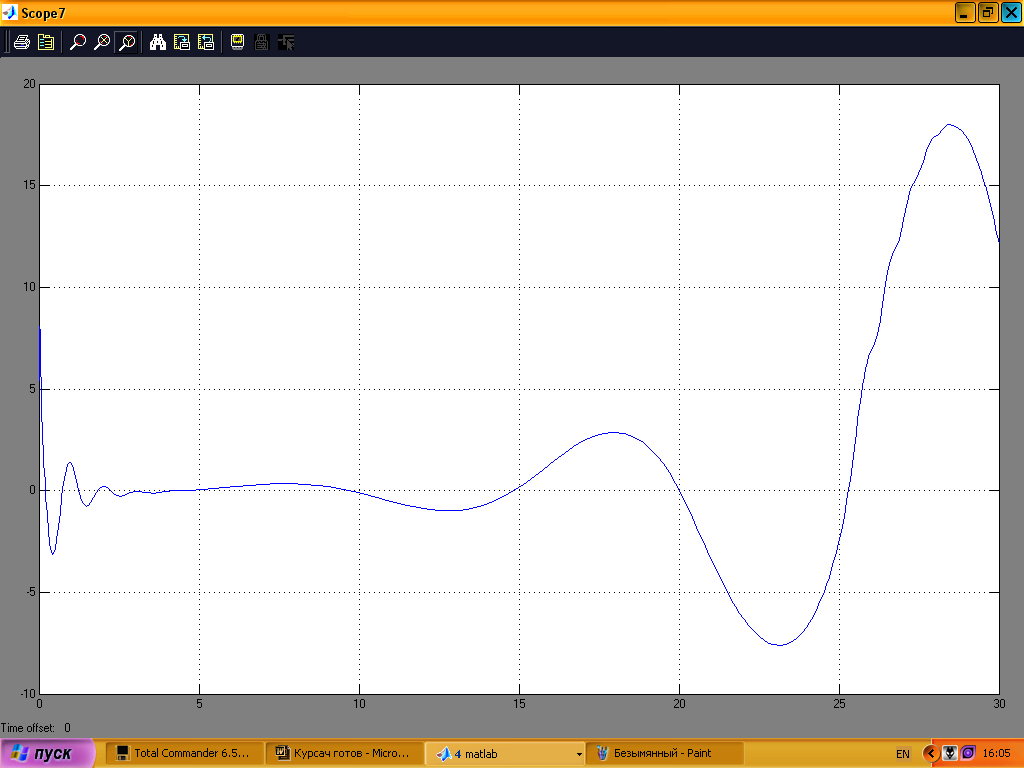
Рис. 19

В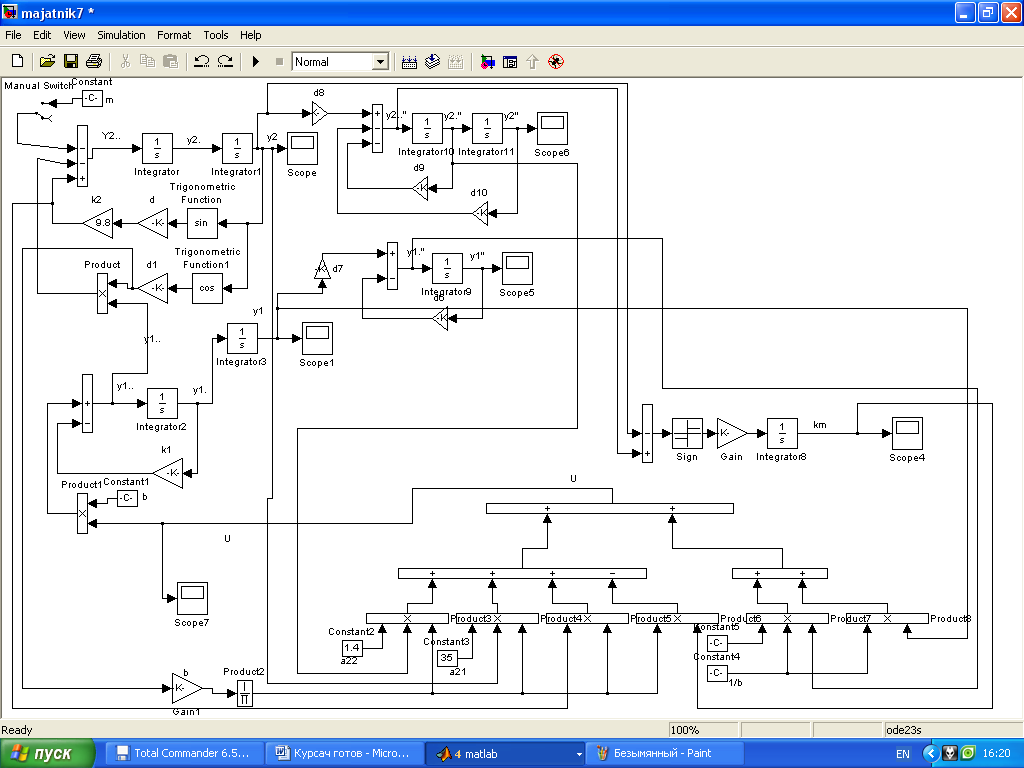третьому наближенні модель системи підтримує стійке положення оберненого маятника в невеликому діапазоні початкових кутів та виявляється стійкою по куту відхилення, але платформа постійно дрейфує з невеликою швидкісю незмінною за напрямом.

Модель системи 3

Ефективна довжина маятника- 0.67 м.

Маса маятника – 0.05 кг.

Маса візка – 0.8 кг.

Початковий кут відхилення – 0.2 рад.

На рис.20 показана зміна початкового кута нахилу, на рис.21 переміщення платформи, на рис.22 керуючий сигнал; графіки подані дня проміжку часу 0–10с.

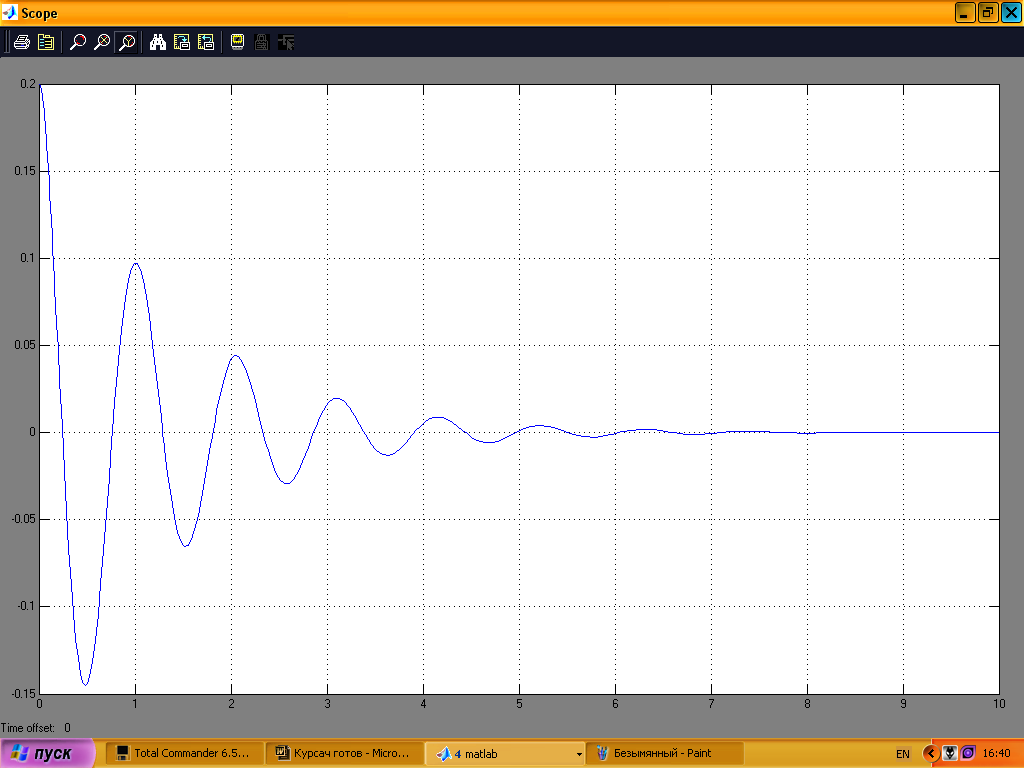
Рис. 20

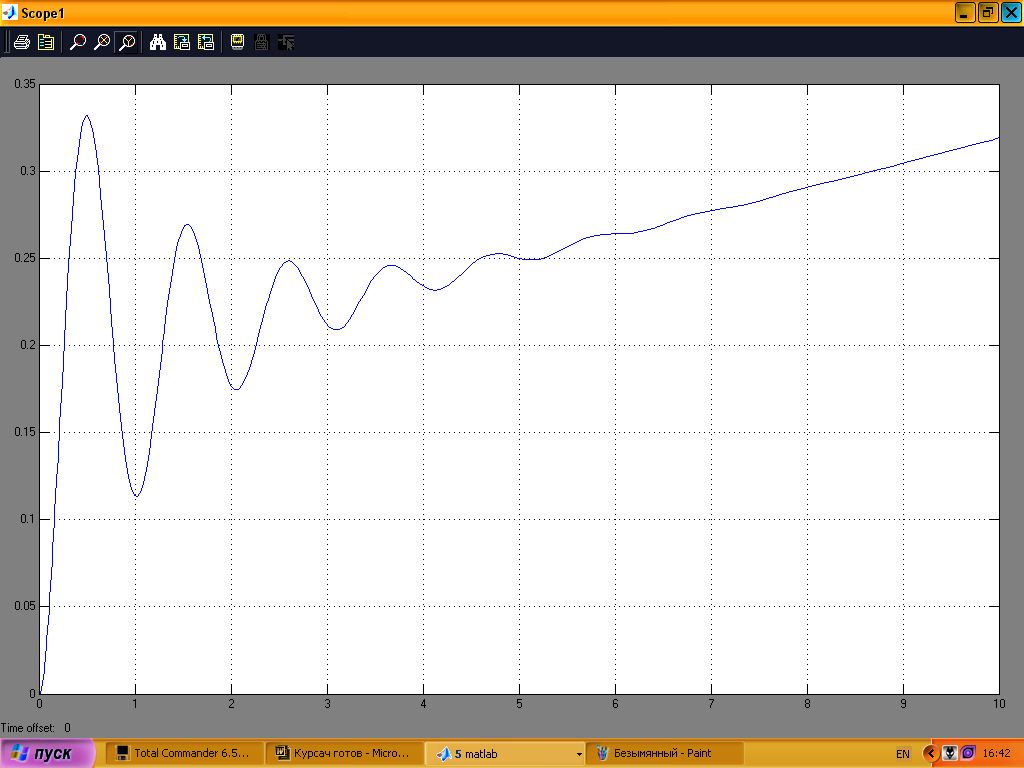
Рис. 21

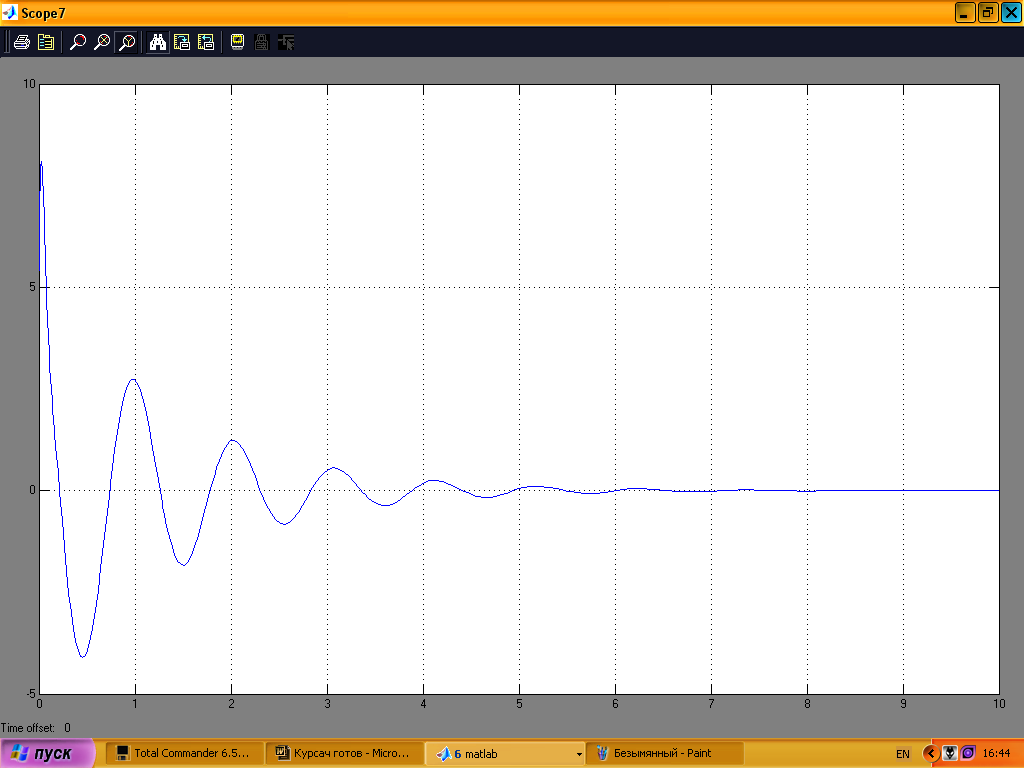
Рис. 22

IV. СТАБІДІЗАЦІЯ ОБЕРНЕНОГО МАЯТНИКА ЗА ДОПОМОГОЮ

ПД-РЕРУЛЯТОРА

С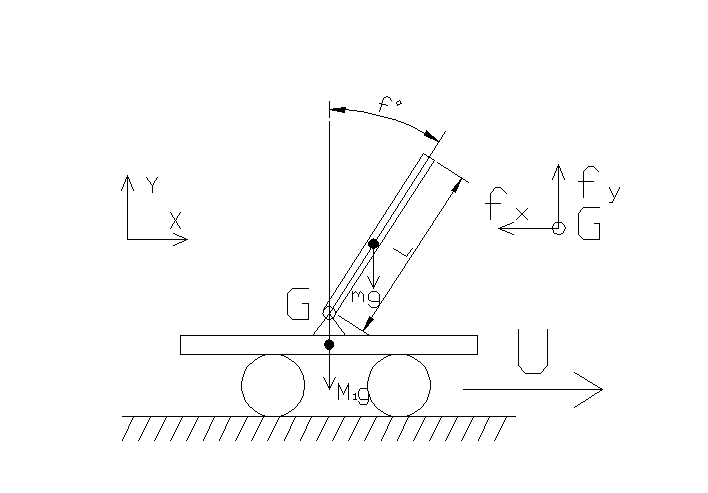истема маятник-візок

Для постановки задачі керування скористаємось системою маятник-візок наведеною вище.

f= – кут відхилення маятника;

М – маса платформи;

м – маса візка;

U – управляюча сила ()

L – довжина маятника;

g – прискорення вільного падіння;

Запишемо рівняння руху використовуючи наведені вище позначення:

4.1

де .

Запишемо проекції сил на осі х та у в точціG:

4.2

Проекція управляючої сили на вісь х:

4.3

Для спрощення задачі стабілізації побудуємо систему з урахуванням наближення:

п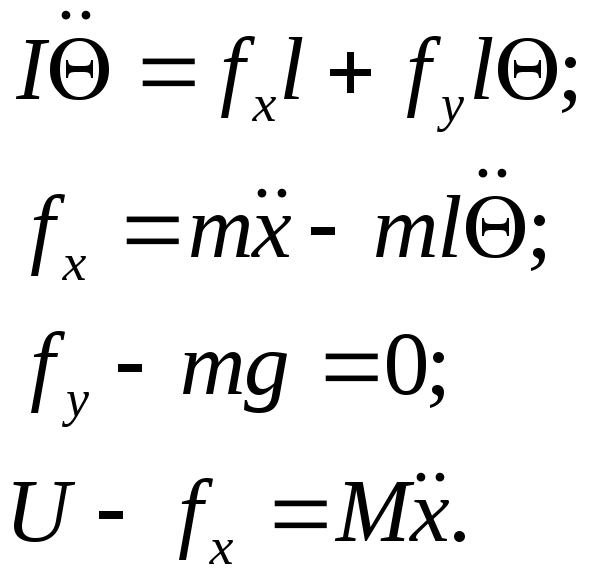ри малих кутах відхилення маятника, виконується .

4.4

Підставимо значення /4.4/ в рівняння /4.1/:

4.5

Управляючий сигнал:

4.6

Як бачимо рівняння /4.6/ функція ПД-регулятора.

Можна вибрати , це достатня умова для того щоб корені характеристичного рівняння /4.7/ були від’ємні.

4.7

За таких умов підставимо в рівняння /4.5/:

Даний алгоритм керування на основі ПД-регулятора дозволяє за короткий проміжок часу повністю стабілізувати систему. Це легко показати за допомогою моделювання.

V. МОДЕЛЮВАННЯ СИСТЕМИ КЕРУВАННЯ ПД-РЕГУЛЯТОРА В СЕРЕДОВИЩІ MATLAB.

Ефективна довжина маятника - 1 м.

Маса маятника – 0.035 кг.

Маса візка – 0.7 кг.

Початковий кут відхилення – 0.15 рад.

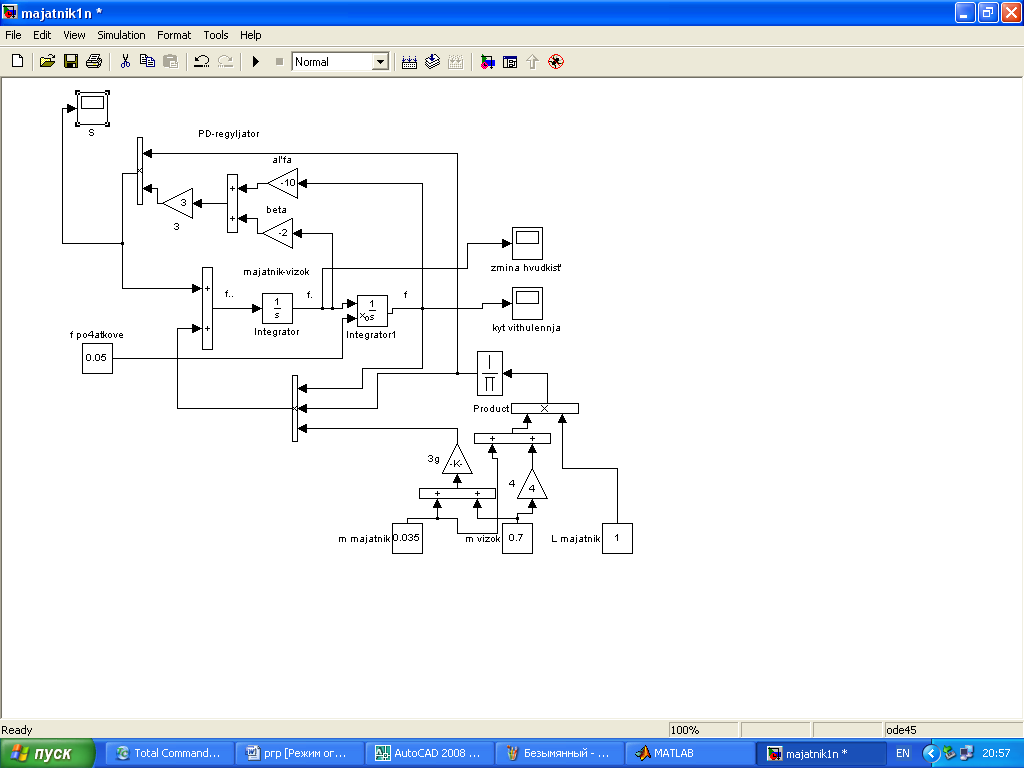
На рис.23 показана зміна початкового кута нахилу, на рис.24 переміщення платформи, на рис.25 зміна швидкості кута ; графіки подані для проміжку часу 0–10с.

Рис. 23

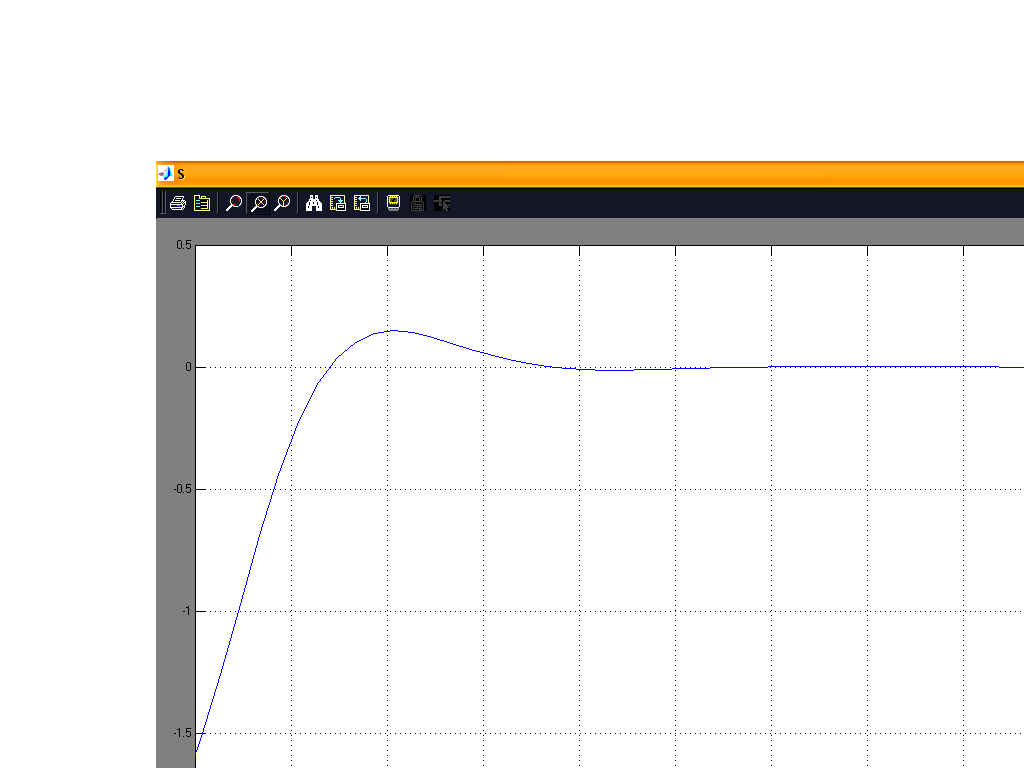
Рис. 24

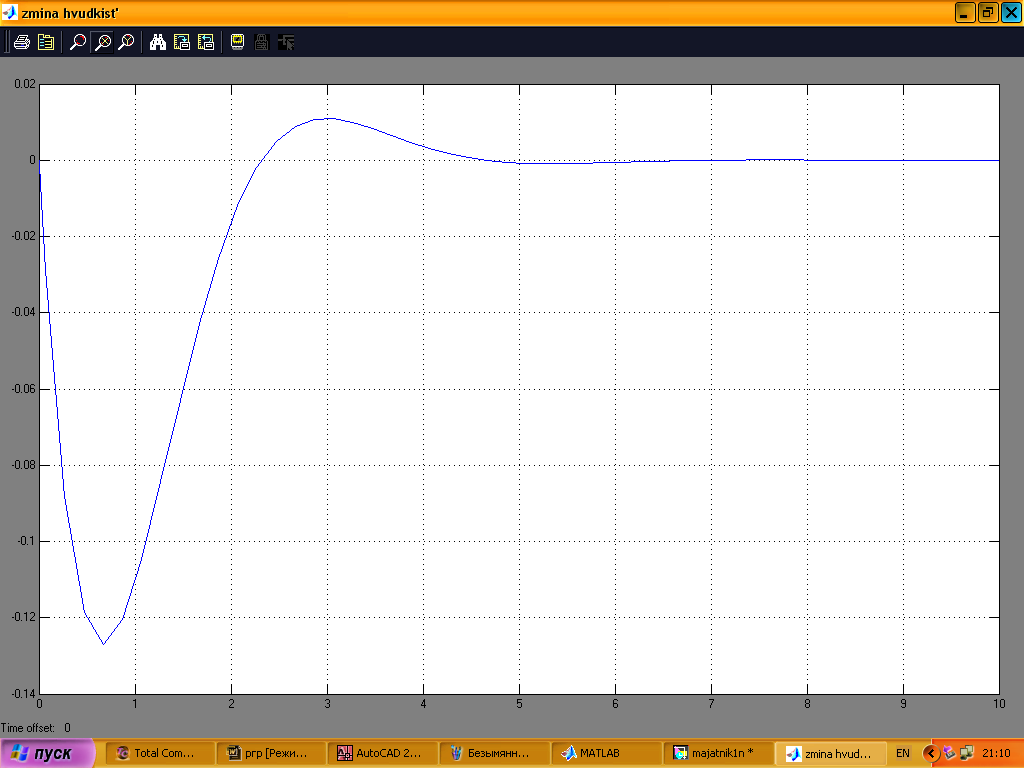
Рис. 25

VI. РЕАЛІЗАЦІЯ СИСТЕМИ МАЯТНИК-ВІЗОК

Для реалізації вище зазначених принципів керування використаємо стандартну схему керування ПД-регулятора.

Каретка (візок) реалізується через платформу що приводиться в зворотно-поступальний рух по направляючих на підшипниках кочення через кінематичний зв'язок з редуктором двигуна. Критерії вибору каретки мінімальна маса та мінімальний момент тертя.

Редуктор реалізується за умовами критерію мінімальної похибки та являє собою двоступеневий редуктор з зубчатими колесами евольвентного зачеплення.

В даному пристрої використовується керований двигун постійного струму серії ДПМ, вибір двигуна здійснюється по критеріям достатньої потужності та швидкодії.

Як слідкуючий пристрій використовується датчик кута типу СКТ. Вибір датчика кута здійснюється за критеріями достатньої точності та швидкодії.

1.Вибір двигуна.

Визначимо необхідну потужність двигуна для відпрацювання сигналу керування:

6.1

де: N – потужність, F – необхідна сила, V – швидкість руху платформи.

6.2

де: m – маса рухомої частини, -прискорення.

Підставимо позначення /6.2/ в формулу /6.1/, отримаємо:

6.3

Визначимо параметрами системи: маса рухомої частини 0,7 кг., максимальна швидкість 1,5 м/с, максимальне прискорення 2 м/.

Отримаємо: Nд [N] , [N] = 2,1 Вт.

Заданим умовам відповідає двигун ДПМ-30N1. Це керований двигун постійного струму що може працювати у реверсному режимі. Його номінальні оберти становлять 4500 об/хв., потужність 9 Вт.

2. Розрахунок редуктора.

В приладобудуванні розбивка загального передаточного типу по ступеням реалізується, в основному, за умовою мінімізації похибки передачі. Тоді оптимальне число ланок n_опт редуктора:

,

- загальне передатне відношення редуктора.

Виходячи з необхідної нам швидкості переміщення платформи (1,5 м/с), швидкість обертання зубчатого колеса на виході з редуктора має становити

750 об/хв.

З конструктивних міркувань виберемо двоступеневий редуктор з передатними числами: на першій ступені 4, на другій 1,5; .

3. Вибір датчика кута.

Так як кути відхилення маятника невеликі (до 0.2 рад) а точність їх визначення має бути достатньою (±0.5% ) використаємо датчик кута серії СКТ.

Задовольняє умовам датчик СКТ-225 2П, з параметрами:

• номінальна напруга 36В;

• робочий діапазон напруг 7-38В;

• опір 5100 Ом;

• похибка відображення 5´;

• ЕРС квадратурної обмотки 200 мВ;

• довготривалий режим роботи.

• крутизна 7 мВ/кут.хв.

VII. ЕКОНОМІЧНА ЧАСТИНА

7.1 Оцінка рівня якості виробу

7.1.1 Вихідні положення

Оцінка рівня якості виробу (приладу, системи, програмного продукту) проводиться з метою порівняльного аналізу і визначення найбільш ефективного в технічному відношенні варіанта інженерного рішення. Така оцінка проводиться на стадіях створення нової і модернізації діючої техніки, при впровадженні її у виробництво, в процесі проведення функціонально-вартісного аналізу тощо.

На різних етапах оцінка рівня якості виробу має свої особливості.

На стадії створення нових або модернізації діючих виробів, коли за варіантами, що підлягають розгляду, недостатньо інформації щодо кількісної характеристики властивостей виробу, узагальнюючий показник рівня якості – коефіцієнт технічного рівня (К_Т.Р.) розраховується для кожного варіанту інженерного рішення за формулою:

(1)

де - коефіцієнт вагомостіi-го параметру якості в сукупності прийнятих для

розгляду параметрів якості;

- оцінка і-го параметру якості j-го варіанту виробу в балах;

n- кількість параметрів виробу, які прийняті для оцінки.

Кращим варіантом інженерного рішення виробу з прийнятих до розгляду є варіант, якому відповідає найбільше значення коефіцієнта технічного рівня:

, (2)

де k – кількість варіантів інженерних рішень, які були прийняті для порівняльної

оцінки.

При наявності кількісної характеристики властивостей виробу коефіцієнт технічного рівня можна визначити за формулою:

(3)

де - відносний (одиничний)і – й показник якості j – ого варіанту виробу.

7.1.2 Обґрунтування системи параметрів виробу і визначення відносних показників якості

На основі даних про зміст основних функцій, які повинен реалізовувати виріб, вимог замовника до них, а також умов, які характеризують експлуатацію виробу, визначають основні параметри виробу, які будуть використані для розрахунку коефіцієнта технічного рівня виробу. Система параметрів, що прийнята до розрахунків, повинна достатньо повно характеризувати споживчі властивості виробу. Чим більше параметрів прийнято для оцінки рівня якості, тим точніша буде оцінка.

Відносні (одиничні) показники якості за будь-яким параметром q_i , якщо вони знаходяться у лінійній залежності від якості, (3) визначаються за формулами:

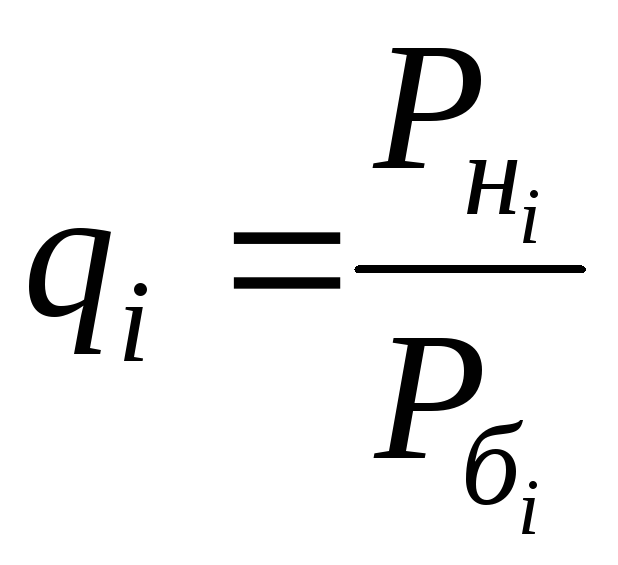(4)

або

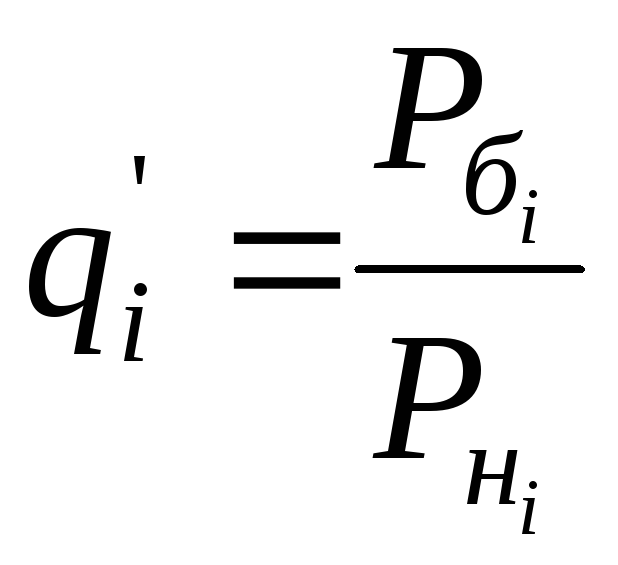(5)

де ,- числові значення і–того параметру відповідно до нового і базового виробів.

При нелінійній залежності між параметрами і якістю виробу або коли параметри відрізняються більш ніж на порядок, слід використовувати наступні формули:

(6)

або

(7)

чи інші залежності, що відповідають специфіці параметру.

Причому величина q_i повинна бути більше одиниці, якщо проходить покращення і – того показника, і менше одиниці, якщо проходить погіршення і – того показника.

У якості базової моделі обираємо Система стабілізації оберненого маятника 1С.

Таблиця 7.1. Технічні характеристики системи

№	Параметри	Одиниці виміру	Вироби
			Система стабіліза- ції оберненого маятника 1СМ	Система стабіліза- ції оберненого маятника 1С
1	Маса маятника	кг	0,05	0,1
2	Маса платформи	кг	0,7	1
3	Максимально- допустимий кут	рад.	0,2	0,07
4	Похибка датчика кута	%	0,2	0,7
5	ККД редуктора	%	92	79

; ;;

; ;

Відносні показники якості

№	Параметри	Вироби
		Система стабіліза- ції оберненого маятника 1СМ	Система стабіліза- ції оберненого маятника 1С
1	Маса маятника	0,5	1
2	Маса платформи	0,7	1
3	Максимальнио- допустимий кут	2.86	1
4	Похибка датчика кута	0,2	1
5	ККД редуктора	1.16	1

7.1.3 Визначення коефіцієнтів вагомості параметрів.

Вагомість кожного параметра в загальній кількості параметрів, що розглядають при оцінці, визначається методом попарного порівняння. Оцінку проводить експертна комісія, кількість членів якої повинна дорівнювати непарному числу.

Визначення коефіцієнтів вагомості передбачає:

- визначення ступеня важливості параметрів шляхом присвоєння їм відповідних рангів;

- перевірку придатності експертних оцінок для подальшого використання;

- виявлення і оцінка попарного пріоритету параметрів;

- обробку результатів і визначення коефіцієнтів вагомості ().

Сума коефіцієнтів вагомості всіх показників дорівнює одиниці.

Після детального обговорення та аналізу кожний експерт оцінює ступінь важливості параметрів шляхом присвоєння їм рангів.

Результати ранжирування параметрів

Таблиця 7.3.

№	Назва параметру	Ранг параметру за оцінкою експерту					Сума рангів, Ri	Відхилення
		1	2	3	4	5
1	Маса маятника	4	4	5	4	5	22	7	49
2	Маса платформи	2	1	2	1	1	7	-8	64
3	Максимальнио- допустимий кут	3	3	2	3	2	13	-2	4
4	Похибка датчика кута	5	5	5	5	4	24	9	81
5	ККД редуктора	1	2	1	2	3	16	1	1
	Всього	15	15	15	15	15	75	0	199

Визначення можливості використання результатів ранжирування параметрів для подальших розрахунків проводять на підставі розрахунку коефіцієнта конкордації (узгодженості) експертних оцінок. Для цього:

а) визначають суму рангів кожного показника (за рядками):

(8)

де r_ij – ранг і- го параметра, визначений j- м експертом;

N – число експертів.

Проводять перевірку загальної суми рангів, яка повинна дорівнювати:

; (9)

б) обчислюють середню суму рангів (Т) за формулою:

(10)

в) визначають відхилення суми рангів кожного параметра (R) від середньої суми рангів (Т):

(11)

г) обчислюють квадрат відхилень за кожним параметром () та загальну суму квадратів відхилень:

(12)

д) визначають коефіцієнт узгодженості (конкордації) за формулою:

(13)

Думку експертів погоджено, так як , де= 0,67 – допустимий коефіцієнт конкордації.

Використовуючи отримані від кожного експерту результати ранжирування параметрів, проводиться попарне порівняння всіх параметрів і результати заносяться до таблиці 5.4.

Таблиця1.4.

Попарне порівняння параметрів

Параметри	Експерти					Підсумкова оцінка	Числове значення коефіцієнтів переваги
	1	2	3	4	5
Х1 і Х2	<	<	<	<	<	<	0.5
Х1 і Х3	<	<	<	<	<	<	0.5
Х1 і Х4	>	>	=	>	<	>	1.5
Х1 і Х5	<	<	<	<	<	<	0.5
Х2 і Х3	>	>	=	>	>	>	1.5
Х2 і Х4	>	>	>	>	>	>	1.5
Х2і Х5	<	<	<	<	>	<	0.5
Х3і Х4	>	>	>	>	>	>	1.5
Х3і Х5	<	<	<	<	>	<	0.5
Х4і Х5	<	<	<	<	<	<	0.5

Визначимо попарний пріоритет пари показників за наступними правилами:

1. Якщо із пари показників, що розглядаються, перший більш вагомий по відношенню до порівнювального, то йому присвоюється знак „>”, інакше – „<”, якщо рівноцінний – „=”;

2. Проставлені знаки попарного пріоритету піддаються подальшій обробці двома способами:

а) оцінка по підсумковому знаку ґрунтується на використанні усередненої думки всіх експертів; якщо початковий показник отримав знак „>”, то пріоритет оцінюється значенням 1,5; якщо початковий показник отримав знак „<”, то пріоритет оцінюється значенням 0,5.

б) оцінка обліку знаку кожного коефіцієнта:

- за кожний знак „>” присвоюється оцінка;

- за кожний знак „=” присвоюється оцінка;

Розрахунок коефіцієнтів вагомості виконується наступним чином: до матриці значень оцінок заносяться відповідні значення попарного пріоритету показників. Значення коефіцієнтів кожного показника на першому етапі розрахунку визначається як відношення часткової суми по строчці до загальної суми. З метою отримання найбільш достовірної оцінки пріоритету показників виконується другий етап розрахунку. Для цього по кожному показнику знаходимо суму множників на відповідні часткові суми, отримані на першому етапі. Якщо результати відрізняються більш ніж на 0,02, то виконується третій етап. Алгоритм третього етапу аналогічний другому.

Розрахунок вагомості параметрів

	Х1	Х2	Х3	Х4	Х5	1 ітерація			2 ітерація		3 ітерація
Х1	1	0.5	0,5	1,5	0,5	4	0,16	17,5		0,152	80,25	0,156
Х2	1.5	1	1,5	1,5	0,5	6	0,24	27,5		0,239	124,75	0,242
Х3	1,5	0,5	1	1,5	0,5	5	0,2	22		0,191	100	0,194
Х4	0.5	0,5	0,5	1	0,5	3	0,12	14		0,122	64,5	0,125
Х5	1,5	1,5	1,5	1,5	1	7	0,28	34		0,298	155,5	0,302
						25	1	115		1	515	1

Розрахуємо коефіцієнт технічного рівня : ,

0,156·0,5+0,242· 0,7+0,194· 2,86+0,125·0,31+0,303 ·1,16=1,1940

По отриманому коефіцієнту можна зробити висновок, що за вагомістю параметрів, які аналізувалися, спроектований прилад є кращим за базовий.

7.2 Витрати на дослідно-конструкторську роботу

Кошторис розробляється виконавцем робіт на основі календарного плану робіт (сітьового графіка) і затверджується замовником або органом, що забезпечує фінансування робіт.

Витрати, що включаються у собівартість ДКР, групуються відповідно до їх економічного змісту за елементами, які наведені далі.

7.2.1 Матеріальні витрати (з відрахуванням вартості зворотних відходів)

Таблиця 4.1.

Матеріальні витрати.

Назва виробу	Стандарт	Одиниця виміру	Кількість	Ціна одиниці, грн.	Сума, грн.
Ватман	ДСТУ 4.454-86	шт.	20	3	60
Гумка	ДСТУ 83.140	шт.	4	1	4
Картридж для принтеру	ДСТУ 37.100	шт.	1	200	200
Папір для принтеру	ГОСТ 1342-78 ДСТУ 1342-94	упаковка	2	25	50
Дискети		шт.	10	2,5	25
Ручка	ДСТУ 95.124-92	шт.	25	1	25
Олівці	РБО249-92 (ІСО 9177-289)	шт.	10	1,2	12
Всього	376
Невраховані витрати	60
Всього	436
Транспорт	50
Загалом	486

7.2.2. Витрати на оплату праці.

Перед визначенням втрат на оплату праці необхідно скласти таблицю яка буде заключати в собі список та зміст робіт. Ці дані зведено в таблиці 5.2.2.

1	Підготовка технічного завдання
2	Складання плану проведення ДКР
3	Пошук і аналіз літератури
4	Дослідження методів стабілізації
5	Огляд і аналіз патентів і промислових зразків
6	Вибір і обґрунтування методів і шляхів його покращення через використану літературу
7	Вибір і обґрунтування схеми комбінованої структурної із поліпшеними характеристиками
8	Розрахунок функції блока керування
9	Розрахунок похибок блока керування
10	Розрахунок основних конструктивних елементів блока керування
11	Розрахунок окремих вузлів блока керування
12	Вибір і розрахунок схеми блока керування
13	Енергетичний розрахунок приладу, вибір і розрахунок параметрів джерела живлення
14	Вибір і розрахунок датчика кута
15	Вибір і розрахунок системи підсилення
16	Вибір і розрахунок системи обробки сигналів
17	Вибір і розрахунок системи управління роботою приладу і стабілізації параметрів
18	Креслення схеми та її елементів
19	Креслення загального вигляду приладу
20	Креслення елементів приладу
21	Складання кошторису
22	Здача роботи замовнику

До цього елемента належать витрати на виплату основної і додаткової заробітної плати виконавців, нараховані відповідно до систем оплати праці, які прийнять в організації, включаючи усі види матеріальних витрат і грошових доплат.

Основна заробітна плата розраховується на основі даних про трудомісткість окремих робіт (наприклад, встановлених у сітьовому графіку) і посадових окладів основних виконавців ДКР. Інформацію про трудомісткість робіт зводять у таблицю 2.2.2.

Таблиця 7.5.

Трудомісткість виконання робіт

Шифр роботи	Трудомісткість, людино-дні				Всього, людино-дні
	Керівник групи	Конструктор I категорії	Конструктор II категорії	Технік
1	2	1	-	-	3
2	3	2	-	-	5
3	8	-	40	-	48
4	5	25	-	-	30
5	-	40	-	-	40
6	6	13	12	-	31
7	2	8	5	-	15
8	-	10	-	2	12
9	-	-	10	2	12
10	2	12	12	20	46
11	-	12	-	12	24
12	1	-	1	5	7
13	-	1	4	8	13
14	-	2	-	10	5
15	-	2	5	-	7
16	1	5	-	-	6
17	3	10	10	5	28
18	-	-	1	6	7
19	-	-	2	1	3
20	1	5	5	5	16
21	6	2	-	-	8
22	3	3	1	1	8
Всього	46	130	127	78	381

Денну заробітну плату визначають виходячи зі щомісячних окладів, враховуючи тривалість робочого місяця 25,4 днів – при 6-ти денному робочому тижні. Результати розрахунків основної заробітної плати виконавців зведені у таблиці 10.

Таблиця 4.6.

Основна заробітна плата виконавців

Посада	Щомісячний оклад, грн.	Денна заробітна плата, грн.	Трудомісткість, людино-дні	Основна заробітна плата, грн.
Керівник групи	5000	196,85	46	9055,1
Конструктор І категорії	3600	141,7	130	18421
Конструктор ІІ категорії	3200	125,98	127	15999,46
Технік	1500	59,055	78	4606,29
Всього	48081,85

Додаткова заробітна плата (премії, одноразові заохочення та ін.) розраховуються згідно з нормативом, який встановлює підприємство і який становить 25% від основної заробітної плати – 12020,46 грн. Сума основної та

додаткової заробітної плати складає витрати за статтею “Заробітна плата” або фонд оплати праці.

Таким чином сума основної та додаткової заробітної плати становить –60102,31 грн.

До цього елемента належать витрати на виплату основної і додаткової заробітної плати виконавців, обчислені згідно із системами оплати праці, прийнятими в організації, включаючи всі види матеріальних та грошових доплат.

Основна заробітна плата розраховується на основі даних про трудомісткість окремих робіт і посадових окладів основних виконавців ДКР.

7.2.3. Відрахування на соціальні заходи

До цього елемента належать витрати, які здійснюються у порядку та розмірах, передбачених законодавством України:

• на обов’язкове державне пенсійне страхування (33,2%) - 19953,96 грн.;

• на обов’язкове державне соціальне страхування (4,6%) – 2764,7 грн.;

Всього відрахування (37,8%) – 22718,67 грн.

7.2.4. Витрати на спеціальне обладнання

У цій статті розраховуються витрати на придбання машин, приладів та іншого обладнання, яке необхідне тільки для цієї НДР. Розрахунок витрат на придбання обладнання проводиться так само, як для витрат на покупні вироби з обов’язковим урахуванням транспортно-заготівельних витрат. Звичайне обладнання, необхідне для оснащення лабораторій, робочих місць та для інших цілей в цю статтю не включають.

У нашому розрахунку ці витрати не передбачені.

7.2.5. Витрати на службові відрядження

Витрати на службові відрядження складаються з фактичних витрат на відрядження штатних працівників, зайнятих виконанням ДКР: витрат на проїзд до місця відрядження і назад, витрат на проживання у готелі, добові витрати, які розраховуються за кожний день перебування у відрядженні, враховуючи перебування у дорозі.

Таблиця4.5

Витрати на відрядження

Посада відряд- жуваного	Оклад місяч-ний, грн.	Пункт відряд- ження	Кількість відряд-жень та трива-лість	Сума проїз ду, грн.	Квар- тиро-ві, грн.	Добо-ві, грн.	Загаль-на сума, грн.
Керівник	5000	м.Херсон	1 на 3 дні	300	700	150	1150,00
Конструктор	3200	м. Херсон	1 на 4дні	250	900	150	1300,00
Всього	2450,00

7.2.6. Експериментально-виробничі витрати

Експериментально-виробничі витрати включають витрати на виготовлення стендів, дослідних зразків, окремих вузлів, деталей та ін., коли вони виготовляються в інших самостійних відділах або в інших організаціях.

Ця стаття враховує витрати на оплату машинного часу, пов’язаного з підготовкою і налагодженням програм. Витрати розраховуються виходячи з кількості годин машинного часу, необхідного для виконання потрібного обсягу обчислювальних робіт за темою і вартістю однієї машинної години.

7.2.7. Накладні витрати

Витрати по цій статті розраховуються за нормативом, встановленим на підприємстві по відношенню до заробітної плати, який складає 67%.

Отже сума витрат складає – 40268,55грн.

7.2.8. Прибуток

Прибуток складає 10% від суми витрат (п.п.2.1.-2.7. –126025,53) і дорівнює - 12602,55 грн.

7.2.9. Загальні витрати

Загальні витрати становлять суму п.п.2.1-2.8 – 138628,08грн.

7.2.10. Податок на додану вартість (ПДВ)

ПДВ обчислюється в розмірі 20% від суми загальних витрат і становить –27725,62 грн.

7.2. 11. Повна вартість роботи, виконаної власними силами

Повна вартість роботи, виконаної власними силами – це сума статей 2.9 та 2.10. – 166353,7грн..