3. Построение амплитудно-частотной характеристики

По определению АЧХ- это модуль частотной передаточной функции.

T₁ = 36 ^. 10^-4 c T₂ = 118 ^. 10^-4 c

Подставим вместо p i^.ω:

Домножим и разделим на i и подставим численные значения:

Найдем модуль от W(i^.ω):

Теперь с помощью символьного процессора MathCad подставив функцию A(ω) строим график АЧХ. Выберем ω=0, 1..150

Рис.2 АЧХ

4. Построение фазово-частотной характеристики.

По определению ФЧХ – это аргумент частотной передаточной функции. Или ФЧХ — частотная зависимость разности фаз на выходе и входе.

Пусть , тогда

Домножим и разделим на комплексное сопряженное знаменателю, получим:

Теперь с помощью символьного процессора MathCad подставив функцию A(ω) строим график АЧХ. Выберем ω=0, 1..150

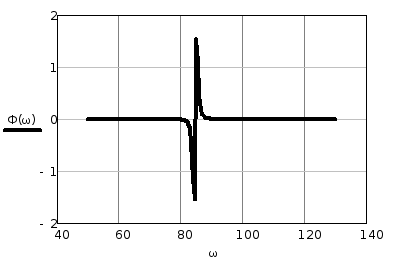
Рис.3 ФЧХ

5. Построение годографа.

_{Сформулируем критерий: для устойчивости замкнутой системы требуется, чтобы амплитудно-фазовая частотная характеристика разомкнутой цепи этой системы не охватывала точку -1}

_T1=0.0036

_{T2= 0.0118}

Подставив численные значения, получим

Теперь с помощью символьного процессора MathCad подставив функцию W(i ω) строим график АЧХ

Рис.4 Годограф

Как видно годограф разомкнутой САУ не охватывает точку -1 , отсюда система устойчива.

6. Построение функции переходного процесса.

Дадим определение изображения по Лапласу : Преобразованием Лапласа   называется преобразование, которое  ставит в соответствие функции f(t) действительной переменной t  функцию F(p) комплексной переменной p по формуле 

Обратное преобразование Лапласа определяется как

где , а p₁…p_n - корни знаменателя

Переходной характеристикой называется реакция невозбужденной системы на единичное воздействие h(t).

Определим изображение переходной функции :

Для нашей системы

_T1=0.0036

_{T2= 0.0118}

Изображение переходной функции будет равно

Подставив числовые значения получим

Выполнил обратное преобразование Лапласа с помощью символьного процессора MathCad, в результате получим:

h(t):= H(p) invlaplace,p ->(0.046538-0.15238 i) e^{(-0.3051+84.7452 i) t} +

+(0.0465+0.1524 i) e^{(-0.3051-84.7452 i) t}

15