1.6.2. Діаграма Нікольса.

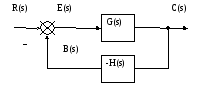
Мал.2. Структурна схема замкненої САУ.

Розглянемо структурну схема замкненої САУ (Мал.2), припускаючи, щоH(s)= -1:

(1.6.2.1.)

Представимо функцію G(jω) у полярних координатах:

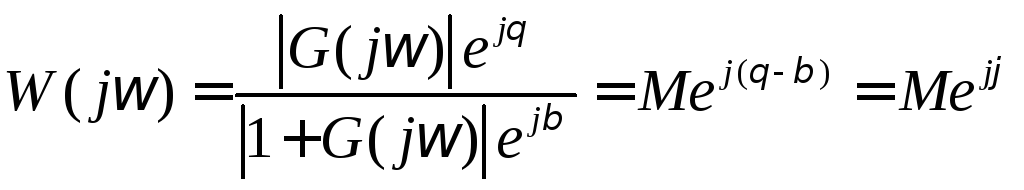; (1.6.2.2.)

Мал.3. Визначення частотних характеристик.

У Рівн.(1.6.2.2.) M – це модуль передаточної функції замкненої САУ, аϕ – аргумент(фазовий зсув).

Годограф точек наS-площині, який відноситься до модулю М з постійними значеннями його амплітуди, називається лінією постійного значення модулю М, або колом з постійним значенням М.

Необхідно довести, що ці лінії є колами.

Нехай

G(jω)=X + jY;(1.6.2.3).

Беручи до уваги Рівн.(1.6.2.2.) ми отримуємо:

Якщо ми перепишемо цей вираз в іншій формі:

X² (M² - 1)+2 M² X+ M² + (M²-1)Y² = 0; (1.6.2.4).

Якщо M≠1 у Рівн.(1.5.7.4), тоді ми маємо:

(1.6.2.5).

Рівн.( 1.5.7.5) – це рівняння кола з наступними характеристиками:

- радіус – [M/(M²-1)];

- координати центру: X= - M²/(M²-1); Y=0.

Якщо M=1 із Рівн.( 1.6.2.4) ми отримуємо значення X= -0.5, тобто рівняння прямої лінії.

Годограф точок на площині G(jω), які відносяться постійних значень фазового зсуву, є також колами.

З урахуванням Рівн.(1.5.7.2.) і Рівн.(1.6.2.3.) ми отримуємо:

(1.6.2.6).

Припускаючи, що N=tg ϕ;

(1.6.2.7).

Із Рівн.(1.6.2.6) і Рівн.(1.6.2.7) ми отримуємо:

(1.6.2.8).

Рівн.(1.5.7.8) є коло з радіусомR=і центром з координатами:

X= -0.5 і Y=1/2N.

Re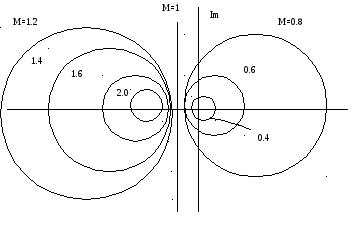

Мал.4. Кола з постійним значенням модулю M.

G(jω)

Мал.5. Кола з постійним значенням фазового зсуву.

Кола з постійним значенням фазового зсуву показані на Мал.12.

W(jω)

Мал.6. Визначення заборонної зони згідно з визначеним показником модулю мM.

Якщо Ви бажаєте скоротити коливальний показник деякої САУ, частотний годограф W(jω) цієї САУ не повинен перетинати коло з визначеним показником М (наприклад, M_max=1.5), який обрано для Вашої САУ.

Для звернення до відповідної програми MatLab6.5 надрукуйте у командному вікні:

num = […];

den = […];

H = tf(num,den) nichols(H); ngrid

Опція ngridзображає діаграму Ніколаса разом з сіткою кривих з постійним значенням коливального показникаM (у dB) і фазового зсуву (у градусах).

180⁰

Мал.7. Визначення запасів стійкості за модулем і фазою за допомогою діаграми Нікольса.

Таким чином, діаграма Нікольса є логарифмічною частотною характеристикою, яка побудована у наступних координатах:

-амплітуда (у dB);

– і фаза (у градусах).

За допомогою діаграми Ніколаса ми маємо и можливість отримати величини запасів стійкості за модулем і фазою.

1.6.3. Властивості кореневого годографу.

А. Загальні положення.

Під час попередніх лекцій Ви дізнались, що стійкість будь-якої САУ визначається головним чином розташуванням коренів характеристичного рівняння цієї САУ на комплексній площині.

Але тільки розташування полюсів, на жаль, не в змозі надати необхідну інформацію відносно кожної складової вільного руху САУ після її замикання з урахуванням процедури лінеаризації.

Коли кожна ланка розімкненої САУ є спочатку стійкою, але після замикання САУ дуже важливу роль відіграють корені з позитивною дійсною частиною, які знаходяться у правій півплощині. Так, наприклад, деякі складові ймовірного вхідного шуму можуть бути значно посилені і це може призвести до різкого зростання вихідної величини.

Нам також дуже важливо провести дослідження, наприклад, як впливає зміна величини підсилення або фазового зсуву однієї із ланок на загальні характеристики всієї САУ – це впливає також на розташування плюсів передаточної функції САУ після її замкнення.

Таким чином, розташування полюсів на S-площині буде постійно змінюватися якщо змінюються параметри САУ і корені характеристичного рівняння цієї САУ будуть описувати на комплексній площині траєкторії, які називаються кореневим годографом.

Приклад 1.

Розглянемо замкнену САУ.

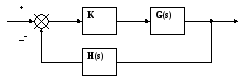
Мал.8. Структурна схема САУ, яка досліджується.

Нехай:

;

Передаточна функція замкненої САУ:

Характеристичне рівняння САУ

Ми маємо встановлений показник: ζ=0.707;

- власна частота коливань.

Тоді ми отримуємо:

= 1.414 and K = 2.

Якщо 0<K≤1 , тоді корені є дійсними і негативними;

Якщо K>1 – тоді корені є комплексними:

При цьому зростання К призведе до зростання показника пере-регулювання і розташування коренів змініться відповідно на комплексній площині.

Якщо K = 1 , тоді САУ має критичне значення показника демпфірування.

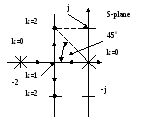
Мал.9. Траєкторія коренів характеристичного рівняння.

Амплітуди цих складових залежатиме від:

1. розташування полюсів передаточної функції замкненої САУ (цю інформацію можна отримати із характеристичного рівняння САУ);

2. розташування нулів передаточної функції замкненої САУ (цю інформацію можна отримати із характеристичного рівняння САУ);

3. характеру вхідного сигналу і початкових умов (цю інформацію не можна отримати із характеристичного рівняння САУ).

Формулювання:

Кореневий годограф – це траєкторія коренів характеристичного рівняння (полюсів передаточної функції) замкненої САУ, коли визначений її параметр змінюється.

Кореневий годограф САУ n-го порядку – це сукупністьn гілок на комплекснійs-площині, які описуютьсяnкоренями характеристичного рівняння, коли визначений її параметр змінюється безперервно протягом всього можливого діапазону його значень.

Метод кореневого годографу дозволяє оцінити чутливість полюсів САУ до зміни будь-якого її параметра. Можна отримати максимальну користь, якщо цей метод використовується у комбінації з критерієм Рауса-Гурвіца.

Цей метод є графічним і дозволяє отримати якісну інформацію щодо стійкості САУ та її динамічних показників. Він може бути застосований як для одно-контурних, так і багато- контурних САУ.

Розглянемо ще раз Мал.15.

Ми припускаємо, що: - 0≤K<∞.

Характеристичне рівняння має наступний вигляд:

1+KG(s)H(s)=0; (1.6.3.1);

де KG(s)H(s) – передаточна функція розімкненої САУ.

Значення кореня належатиме кореневому годографу тоді і тільки тоді, коли воно задовольняє Рівн.( 1.5.8.1) для дійсних значень K, якщо 0≤ K<∞.

Зрозуміло, що K є лінійним параметром Рівн.( 1.6.3.1).

Рівн.(1.6.3.1) може бути надано у наступному вигляді:

;(1.6.3.2)

Звідси, якщо належатиме кореневому годографу, тоді права частина Рівн.( 1.6.3.2) при цьому значеннідає позитивне значення.

Оскільки G(s) і H(s) при деякому значенні у загальному випадку є комплексні величини, тоді Рівн.( 1.5.8.2) розкладається на 2 рівняння:

(1.6.3.3) –амплітудний критерій;

і

(1.6.3.4) –кутовий критерій.

Оскільки ми вважаємо, що 0≤ K<∞, тоді головна умова приналежності до кореневого – це Рівн.( 1.6.3.4).

У загальному випадку ми можемо представити функцію KG(s)H(s)у наступній формі:

Або:

- амплітудний критерій;

-

де q – ціле число.

кутовий критерій;

Оскільки ми маємо 0≤K<∞, тоді Рівн.(1.6.3.3) задовольняє довільним значеннямs_i .

Звідси, умова приналежності точки до кореневого годографу визначається Рівн.(1.6.3.4).

Кутовий критерій показано на Мал.10 для наступної передаточної функції:

(1.6.3.5)

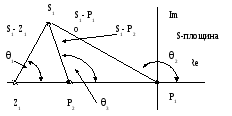
Мал.10. Графічна ілюстрація кутового критерію.

Припустимо, ми бажаємо перевірити, якщо точка належатиме до кореневого годографу.

Ми визначимо кут (або аргумент) співмножника (s₁-z₁) черезθ₁, співмножника (s₁-p₁) черезθ_2,співмножника (s₁-p₂) черезθ₃.

Якщо точка належатиме до кореневого годографу, тоді необхідно виконати умову Рівн. (1.6.3.4).

Тоді для визначення приналежності точки до кореневого годографу необхідно виконати умови Рівн.( 1.6.3.3), тобто:

θ₁-θ₂-θ₃= ± 180⁰;

Годограф, який містить всі точки, які задовольняють цьому відношенню, є кореневим годографом.

Якщо точка належатиме до кореневого годографу , тоді відповідне значенняKвизначається згідно з Рівн.( 1.6.3.2)

;

Примітка: це значення коефіцієнта підсилення K є дійсним і позитивним.

Враховуючи вищевикладене, з метою забезпечення приналежності точки до кореневого годографу, ми повинні виконати наступну умову:

Σ (всіх кутів, які відносяться до кінцевих нулів) - Σ (всіх кутів, які відносяться до кінцевих полюсів)= r(180⁰); де r=±1, ±3, ± 5, …, (1.6.3.6)

(причому ці нулі і полюси відносяться до розімкненої передаточної функції).

В. Властивості кореневого годографу.