Основные понятия корреляционно-регрессионного анализа

1. Среднее значение переменной определяется по следующей

формуле:

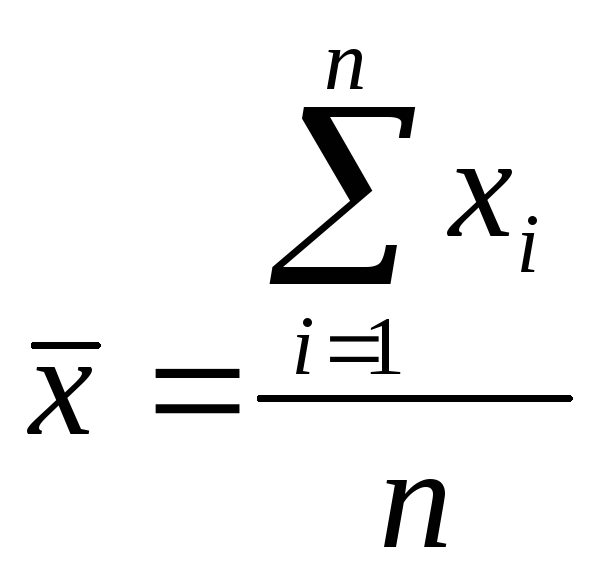, (6.13)

где x_i — эмпирическое значение переменной х;

п — число наблюдений.

2. Дисперсия

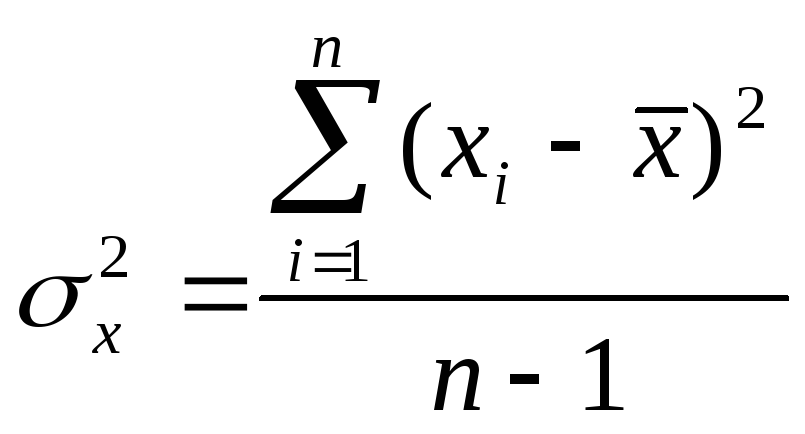(6.14)

3. Ковариация

(6.15)

4. Коэффициент корреляции

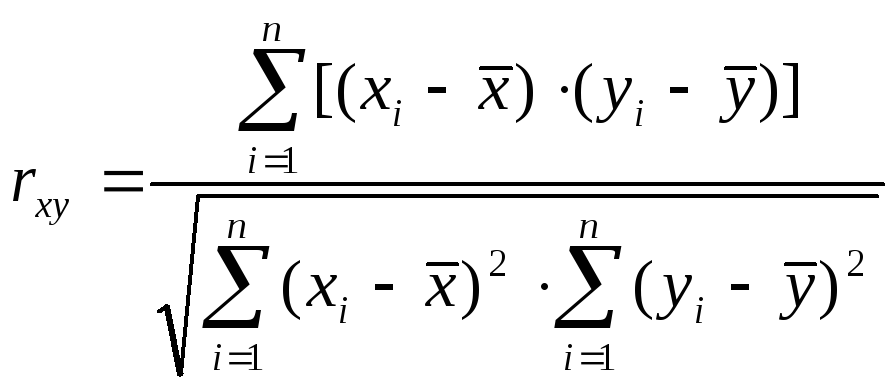(6.16)

Коэффициент корреляции характеризует тесноту или силу свя­зи между переменными у и х. Значения, принимаемые , заклю­чены в пределах от - 1 до + 1. При положительном значении имеет место положительная корреляция, т. е. с увеличением (уменьшением) значений одной переменной (х) значение другой (у) соответственно увеличивается (уменьшается). При отрицатель­ном значении имеет место отрицательная корреляция, т. е. с увеличением (уменьшением) значений х значения у соответствен­но уменьшаются (увеличиваются). При изучении экономического явления, зависящего от многих факторов, строится множествен­ная регрессионная зависимость. В этом случае для характеристи­ки тесноты связи используется коэффициент множественной кор­реляции:

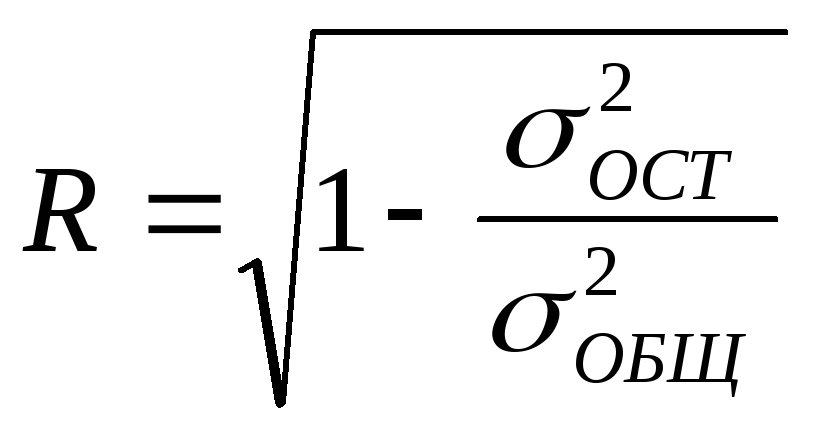(6.17)

где - остаточная дисперсия зависимой переменной;

- общая дисперсия зависимой переменной.

5. Общая дисперсия определяется по формуле:

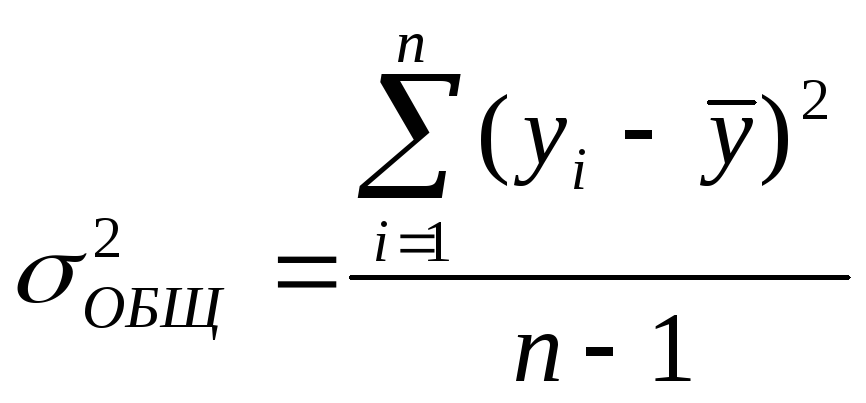(6.18)

Величина характеризует разброс наблюдений фактических значений от среднего значения .

6. Остаточная дисперсия определяется по следующей формуле

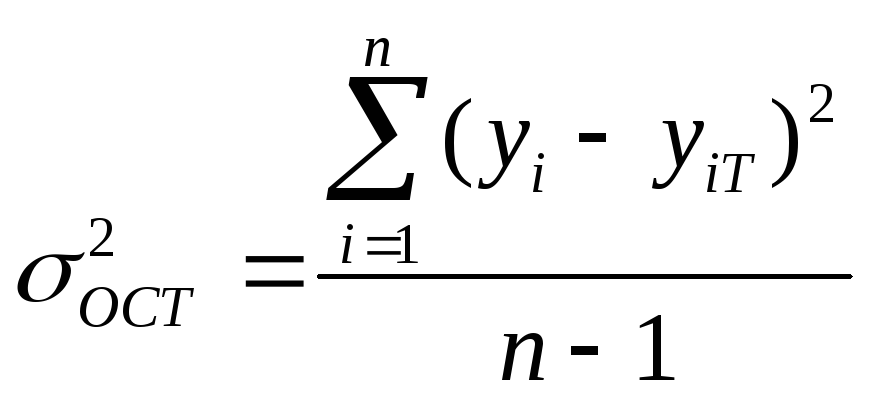(6.19)

где - теоретические значения переменной у, полученные по уравне­нию регрессии (5.1) при подстановке в него наблюдаемых фактических значений х_i.

Остаточная дисперсия характеризует ту часть рассеяния пере­менной у, которая возникает из-за всякого рода случайностей и влияния неучтенных факторов.

7. Коэффициент детерминации служит для оценки точности ' регрессии, т. е. соответствия полученного уравнения регрессии имеющимся эмпирическим данным, и вычисляется по формуле

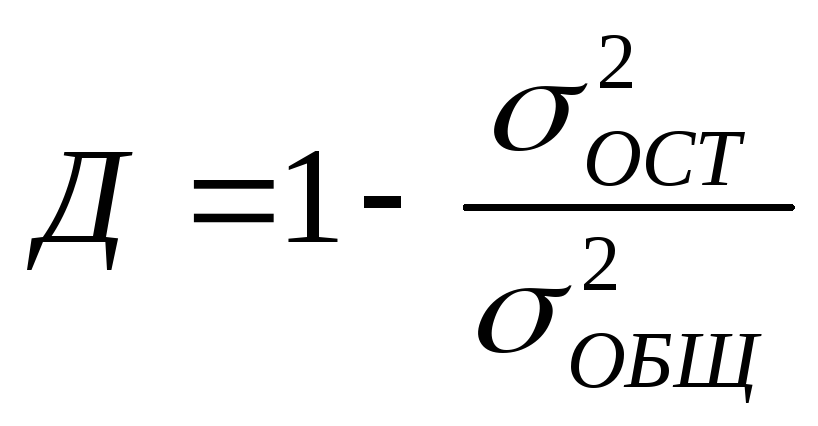(6.20)

Изменяется Д в пределах от 0 до 1, т. е.

Модель считается тем точнее, чем ближе Д к 1, т. е. чем мень­ше .

Стандартная ошибка оценки равна

Если Д = 0, это значит отношение = 1, т. е. = , и, следовательно, . В этом случае прямая регрессии будет параллельна оси X, корреляционно-регрессионная связь между X и Y отсутствует. Если Д = 1, значит, = 0, т. е. = 0. Отсюда наблюдаемые точки лежат на построенной прямой, следовательно, зависимость функциональная.

8. Корреляционное отношение используется для оценки тесно­ты связи между двумя явлениями, в частности для определения тесноты связи исходного ряда у_i с теоретическим рядом . Корре­ляционное отношение определяют по данным, сгруппированным по объясняющей переменной по следующей формуле:

(6.21)

6.2. Исходные предпосылки регрессионного анализа и свойства оценок

Применение метода наименьших квадратов для определения параметров регрессии предполагает выполнение некоторых пред­посылок.

Отметим наиболее существенные из них.

Предпосылка I. При нахождении оценок переменной у предпо­лагается существование зависимости переменной у только от тех объясняющих переменных, которые вошли в модель (регрессию). Влияние прочих факторов и случайностей учитывается случайной возмущающей переменной z. При этом полагаем, что для фиксиро­ванных значений переменных х_i-() среднее значение пере­менной z равно нулю.

Предпосылка 2. Предполагается, что влияние неучтенных фак­торов постоянно. Так, при рассмотрении временных рядов в раз­личные периоды эти неучтенные факторы оказывают одинаковое влияние.

Предпосылка 3. Отсутствует автокорреляция между возмущаю­щими переменными z.

Предпосылка 4. Число наблюдений должно превышать число параметров регрессии, иначе невозможна оценка этих параметров.

Предпосылка 5. Предполагается односторонняя зависимость пе­ременной у от факторов х_i-(), отсутствие взаимосвязи.

Предпосылка 6. Зависимая переменная у и факторы х_i-() распределены нормально.

С помощью регрессионного анализа при указанных выше пред­посылках находят оценки параметров, наиболее хорошо согласую­щиеся с опытными данными. Данные оценки должны обладать оп­ределенными свойствами. Рассмотрим некоторые из этих свойств (без доказательства).

1. Несмещенность оценок параметров регрессии. Оценка параме­тров регрессии называется несмещенной, если для любого фикси­рованного числа наблюдений выполняется равенство математичес­кого ожидания параметра и значения параметра регрессии. Надо отметить, что оценки, полученные методом наименьших квадра­тов, обладают свойством несмещенности.

2. Состоятельность оценок параметров регрессии. Данное свой­ство состоит в том, что с ростом объема выборки оценка парамет­ра регрессии b сходится к теоретическому значению параметра (вычисленного по всей генеральной совокупности), т. е. ошибка оценки стремится к нулю:

(6.22)

3. Эффективность оценок параметров регрессии. Несмещенная оценка параметра регрессии называется несмещенной эффектив­ной, если она среди всех прочих несмещенных оценок этого же па­раметра обладает наименьшей дисперсией.

4. Достаточность оценки. Если представляет собой достаточ­ную оценку параметра , то не существует другой оценки этого па­раметра, которую можно получить по выборке из некоторой гене­ральной совокупности и которая дала бы дополнительную инфор­мацию о нем. Р. Фишер показал, что количество измеримой ин­формации, содержащейся в некоторой оценке, равно обратной величине от ее дисперсии. Таким образом, понятие достаточности эквивалентно требованию минимальной дисперсии. Достаточная оценка с необходимостью должна быть эффективной и, следова­тельно, также состоятельной и несмещенной.