4.1. Усилитель

Звенья, имеющие конечный ненулевой коэффициент усиления постоянного сигнала, то

есть W(0) = k ≠ 0, называются позиционными. Это значит, что числитель и знаменатель переда-

точной функции имеют ненулевые свободные члены (постоянные слагаемые).

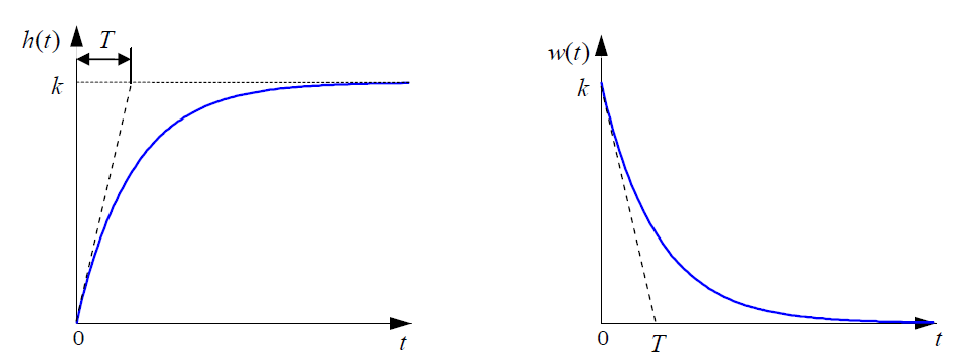
Простейшее позиционное звено – идеальный (безынерционный) усилитель. Его передаточная функция W(s) = k . Строго говоря, он не является динамическим звеном, поскольку изменение выхода происходит мгновенно, сразу вслед за изменением входа. При действии на вход единичного ступенчатого сигнала 1(t) (или дельта-функции δ (t) ) на выходе будет такой же сигнал, усиленный в k раз, поэтому переходная и импульсная характеристики звена равны

h(t) = k (t > 0) и w(t) = k ⋅δ (t) .

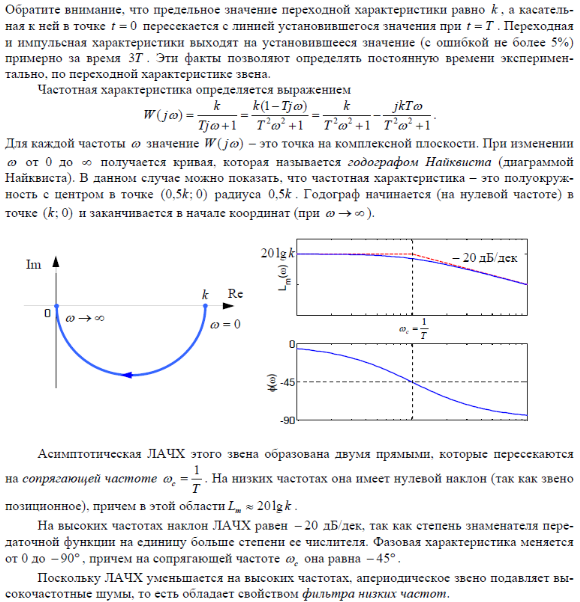
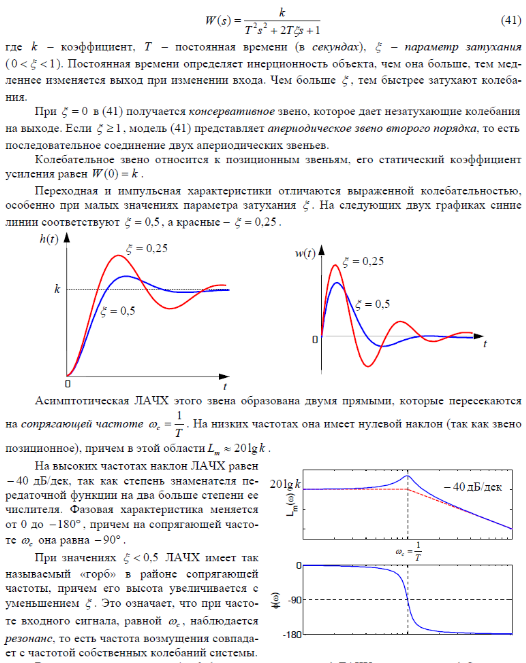
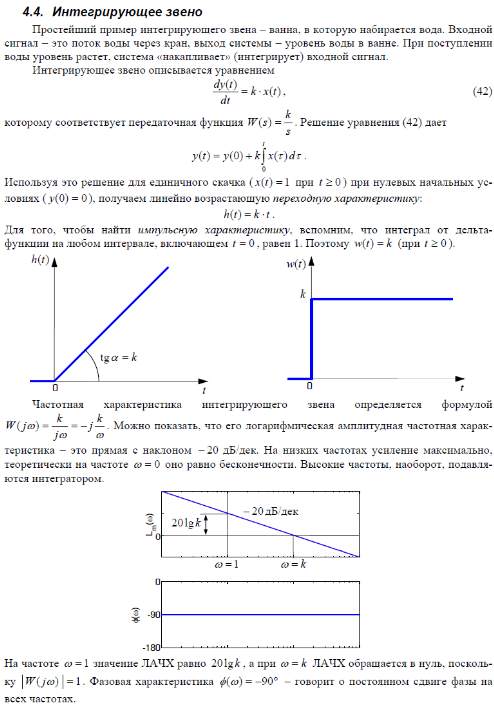
Если на вход усилителя действует синусоидальный сигнал, на выходе он усиливается в k раз без изменения фазы, поэтому амплитудная и фазовая частотная характеристики не зависят от частоты входного сигнала: A(ω) = k , φ (ω) = 0 .

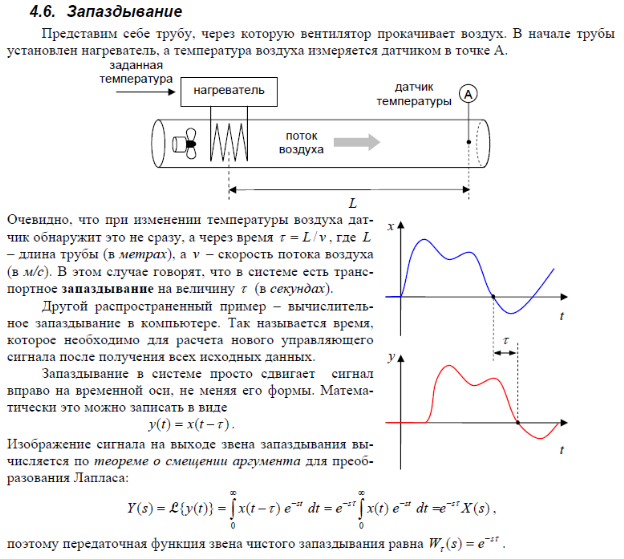
Устойчивость систем автоматического управления и методы её оценки.

Устойчивость – это свойство САУ возвращаться в состояния покоя или установившегося  движения, из которого  система  была выведена каким-либо воздействием после устранения этого воздействия.

Обычно понятие  устойчивости иллюстрируется следующими примерами. Будем считать системой некоторый шар, который может находиться в одном из трех состояний:

1) 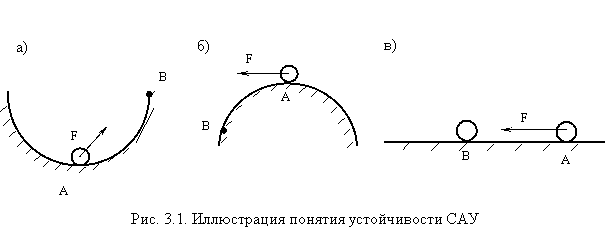     если шар находится на вогнутой поверхности (рис. 3.1, а), то при наличии силы F, соответствующей внешнему воздействию на систему, шар можно вывести из состояния покоя. Если теперь устранить  воздействие F, то шар после совершения нескольких колебаний около точки равновесия А придет в установившееся состояние (или состояние покоя), соответствующее точке А. Это пример устойчивого равновесия – система является устойчивой;

2)      если к шару, находящемуся на выпуклой поверхности (рис. 3.1, б), приложена сила F, то, отклонившись под воздействием этой силы в точку B, шар после прекращения воздействия силы не придет в установившееся положение (в точку А). Такое состояние является неустойчивым;

3) если шар находится на шероховатой ровной поверхности (рис. 3.1, в) и к нему приложена сила F, то шар выйдет из состояния равновесия и после снятия воздействия придет в новое состояние равновесия. В зависимости от величины и знака силы F шар может иметь бесчисленное множество точек равновесия. Такое состояние носит название нейтрально-устойчивого, т.е. система является нейтрально-устойчивой.

Понятие о характеристическом уравнении

Устойчивость линейной системы определяется ее параметрами и не зависит от внешних воздейст­вий. Процессы в САУ описываются неоднородным дифференци­альным уравнением  (2.5),  общее решение которого состоит из двух составля­ющих:

x_вых(t) = x_{вых(вын)}(t) + x_вых(св)(t).                                         (3.1)

Здесь  x_{вых(вын)}(t)  – частное решение уравнения  (2.5), определяемое приложенным к системе внешним воздействием, вследствие чего x_{вых(вын)}(t) называется вынужденной составляющей; x_вых(св)(t)  – общее решение соответствующего уравнению  (2.5) однородного дифференци­ального уравнения

(3.2)

т.е. дифференциального уравнения, правая часть которого равна нулю, следовательно, равны нулю внешнее воздействие x_вх(t) и все ее производные.

Поскольку  только x_вых(св)(t) описывает поведение САУ после устранения внешнего воздействия, эту составляющую в выражении (3.1) называют свободной (переходной)  составляющей.

Очевидно, что линейная система устойчива, если свободная  составляющая с течением времени затухает, т.е.

Х_вых(св)(t) = 0.                                                    (3.3)

Общее решение однородного дифференциального уравнения (3.3) определяется  корнями соответствующего характеристического уравнения:

a_npⁿx_вых(p) +  a_(n-1)p^(n-1)x_вых(p) +…+ a₁px_вых(p) +  a₀x_вых(p) = 0,                 (3.4)

т.е. полюсами передаточной функции замкнутой системы.

Условия устойчивости.

Независимо от выбранного критерия устойчивости первоначально проверяется выполнение необходимого условия устойчивости,согласно которому все коэффициен­ты характеристического уравнения (3.4) должны быть положительными, т.е.

a_i > 0   при   i =1,…,n.                                             (3.6)

Если необходимое условие не выполняется, делается заключение о том, что система неустойчива. В противном случае необходимо переходить к  проверке достаточного условия устойчивости, формулировка которого зависит от выбранного критерия устойчивости. В даль­нейшем будем полагать, что необходимое условие устой­чивости выполняется.

Алгебраический критерий устойчивости Гурвица

Для оценки устойчивости линейной системы по критерию Гурвица необходимо из коэффициентов характеристиче­ского уравнения (3.5) составить определитель Гурвица, размерность которого равна порядку системы.

Определитель  Гурвица имеет вид:

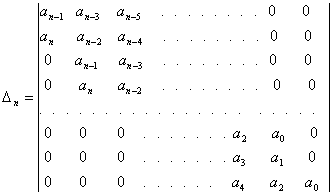.                             (3.8)

 

Порядок составления определителя Гурвица следующий. В качестве элемента первого столбца первой строки определителя записывается коэффици­ент a_n-1, а затем на  главной диагонали располагаются коэффициенты  характеристического уравнения (3.4) с последовательно убывающими индексами. При этом в послед выражении нем столбце последней строки определителя записывается коэффициент .

Затем, начиная от коэффициентов, стоящих на главной диагонали, заполняются столбцы определителя так, чтобы  ин­дексы коэффициентов, расположенных над коэффициентами главной диагонали, последовательно убывали, а коэффициентов, расположенных под диагональными коэффициентами, – последовательно возрастали. Если в процессе заполнения столбца определителя индекс коэффициента достигает значения nили 0, то дальнейшее заполнение столбца осуществляется нулями.

Далее необходимо вычислить значение определителя Гурвица и всех его диагональных миноров, которые получают из определителя (3.8) путем отчеркивания равного числа строк и столбцов в левом верхнем углу определителя. Например, диагональный минор первого порядка равен Δ₁=a_n-1 ; диагональный минор второго порядка:

           Δ₂= 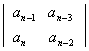,                                                       (3.9)

а диагональный минор третьего порядка:

Δ₃= 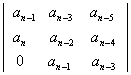.                                                (3.10)

 

 

Очевидно, что диагональный минор n-го порядка совпадает с определителем Гурвица.

Линейная система  устойчива, если при выполнении необходимого условия (3.6), определитель Гурвица и все его диагональные миноры будут положительны.

Пример нахождения минора:

Например, есть матрица:

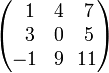
Предположим, надо найти дополнительный минор M₂₃. Этот минор - определитель матрицы, получающейся путем вычеркивания строки 2 и столбца 3:

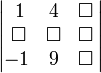
Получаем M₂₃= 13

Частотные критерии устойчивости: Критерий Найквиста.