Передаточные функции и частотные характеристики систем различной структуры

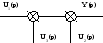
1. Последовательное соединение звеньев.

Пусть

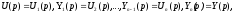
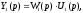
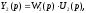
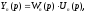
тогда а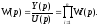

При последовательном соединении звеньев передаточная функция системы равна произведению передаточных функций звеньев, входящих в систему.

Переходная характеристика системы не может быть найдена из переходных характеристик звеньев она определяется специальными методами.

Так как известны передаточные функции звеньев, то известны частотные функции звеньев Wi( j), тогда

Пример 1. Построение АФХ системы, состоящей из 2-х последовательно соединённых звеньев

A₁= A₁₁A₂₁; ₁= ₁₁+₂₁; вычисляем A₂, ₂; A₃, ₃ и т.д. строим АФХ системы.

Пример 2. Построить логарифмические характеристики системы, если заданы ЛЧХ двух последовательно соединенных звеньев.

При последовательном соединении звеньев ЛАЧХ системы получается суммированием ЛАЧХ звеньев.

Сначала проводят горизонтальную линию с ординатой 20lgk, где Затем отмечают сопрягающие частоты, в этих точках происходит излом результирующей ЛАЧХ.

Допущение: используются звенья направленного действия, т.е. отсутствует обратное действие нагруженного выхода на вход.

2. Параллельное включение звеньев.

Определим передаточную функцию системы:

- для параллельного соединения звеньев.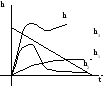

Переходная характеристика системы равна сумме переходных характеристик звеньев, т.е.

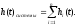
Частотные характеристики:

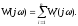
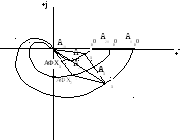
План построения ЛЧХ системы:

1. По ЛЧХ звеньев построить АФХ звеньев.

2. По АФХ звеньев построить АФХ системы.

3. По АФХ системы построить ЛЧХ системы.

3. Встречно-параллельное соединение динамических звеньев.

1. Контур с отрицательной обратной связью.

Сигнал с выхода цепи обратной связи вычитается из входного воздействия, поэтому обратная связь называется отрицательной.

Ф(р) – передаточная функция замкнутой системы (часто обозначается W_з(р)).

Составим систему уравнений контура

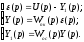
Тогда

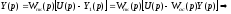
• передаточная функция контура с отрицательной обратной связью.

W_пк(р) – передаточная функция прямого канала,

W_ос(р) – передаточная функция канала обратной связи,

W_пкW_ос(р) – передаточная функция разомкнутой системы.

Правило определения Ф (р) приведено ранее.

Контур с неединичной обратной связью может быть преобразован к контуру с единичной отрицательной обр. связью

где

Эквивалентная структурная

схема контура с ООС.

1. Контур с положительной обратной связью.

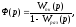
где

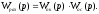
Частотные характеристики контура с ООС.

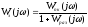–частотная передаточная функция контура.

Рассмотрим три случая при единичной ООС

W_ос(j)=1 Перейдём к логарифмическим характеристикам

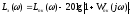
1. Для малых частот, т.е. _среза, 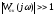(А_пк()1) и единицей можно пренебречь, тогда 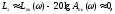т.е. при малых частотах логарифмическая ампл.- част. характ. контура идёт по оси , а передаточный коэффициент замкнутой системыk_з 1.

2. При больших частотах, т.е. _ср., А_пк()1, поэтому величиной А_пк() пренебрегаем, тогда

3. _ср (частоты отличаются на 12 декады). В этом случае пользуются намограммой замыкания (намограммой Никольса).

Преобразование структурных схем.

Используется для упрощения анализа САУ, составления передаточных функций и дифференцианальных уравнений. Преобразования схем проводят так, чтобы контуры не пересекались, а чтобы один контур входил внутрь другого. Закон изменения выходного сигнала не должен изменяться в результате эквивалентного преобразования структуры.

Исходная структура системы	Эквивалентная структура системы
Перенос точки суммирования сигналов со входа на выход Уравнение выходной координаты:	Wф(p) - фиктивная передаточная функция
Перенос точки суммирования сигналов с выхода на вход Уравнение выходной координаты:
Перенос точки съема со входа звена на его выход W(p) Y(p) U1(p) U1(p) W(p) U1 (p) Y(p) = Wф(p) U1(p)

Перенос точки съема сигнала с выход на входа звена. W(p) W(p) U (p) Y(p) W(p) = Wф(p) Y(p) U(p) Y(p) Y(p)
Перестановка сумматоров
Вынос точки разветвления из встречно-параллельного соединения. Y(p) U (p) Wпк (p) Wос(p) E (p) Y(p) U (p) Wпк (p) Wос(p) E (p) Wф(p) =

Пример. Определить передаточную функцию системы заданной структуры путем эквивалентных преобразований к одному звену.

Исходная структурная схема:

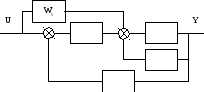
а)

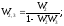
б)

Переносим точку суммирования сигналов

в)

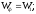
г)

д)

е)

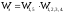
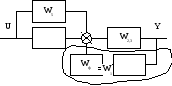
Пример2. Преобразовать заданную структурную схему по каналу возмущения с целью приведения ее к удобному виду для пользования номограммой замыкания.

Исходная структурная схема: W3 W1 U Y W2 F W2 W1 y W3 x W2 W1,3 y F - возмущающее воздействие. Найти передаточную функцию по каналу возмущения предполагаяU(p)=0 (входное воздействие отсутствует), или y - отклонение y только от .	Преобразуем схему: а) W1 для находится в обратной связи. б)
в) W2 x W1,3 y W2 x W1,3 y y W1,2,3 Wраз Wзам д) ЛЧХ контура с ед. отрицательной обратной связью можно найти по ЛЧХ замкнутой системы с использованием номограммы.	г)