Типовые динамические звенья сау

1. Статические (позиционные) звенья:

1. Безынерционное звено.

2. Звено апериодическое I порядка.

3. Звено апериодическое I I порядка.

4. Колебательное звено.

II. Интегрирующие звенья:

1. Идеальное интегрирующее звено.

2. Реальное интегрирующее звено.

III. Дифференцирующие звенья:

1. Идеальное дифференцирующее звено.

2. Реальное дифференцирующее звено.

3. Форсирующее звено.

4. Трансцендентные звенья.

1. Звено запаздывания (чистого запаздывания, транспортного запаздывания).

4. Неустойчивые звенья.

1. Консервативное звено.

2. Звено неустойчивое апериодическое I порядка.

1. Статические (позиционные) звенья.

1. Безынерционное звено.

1. Уравнение связи выход-вход y = ku.

2. Переходная функция h(t)=k1(t)

3. Передаточная функция W(p)=k.

4. Амплитудно-фазовая характеристика

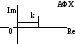
5. Логарифмические частотные характеристики

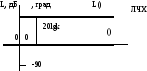
Пример. Усилитель постоянного тока с отрицательной обратной связью (инерционностью усилителя пренебречь).

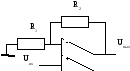
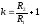
Апериодическое (инерционное) звено I порядка.

2.1. Дифференциальное уравнение

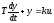
2.2. Переходная функция

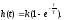
2.3. Передаточная функция

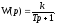
2.4. Амплитудно-фазовая частотная функция (частотная передаточная функция)

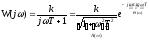
2.5. Логарифмические частотные характеристики

.

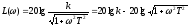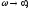При 0 еслито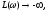

при .

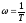
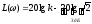Обычно строят асимптотические ЛАЧХ: на стандартной сетке ( с масштабом 1 декада – увеличение частоты в 10 раз – 100 мм, 20 дБ – 40 мм) проводят вертикальную штриховую линию через точку с частотой, называемой сопрягающей, =1/Т. Левее сопрягающей частоты проводят прямую с уровнем 20lgk, а правее с наклоном – 20дБ/дек, соответствующую выражению 20lgk/T. Точная ЛАЧХ будет несколько отличаться от асимптотической, причём наибольшее отклонение будет 3 дБ.

Если проводятся точные расчёты, то строятся точные ЛАЧХ звена Lт(), если приближенные расчёты, то строятся асимптотические ЛАЧХ Lа().

В подавляющем большинстве случаев строятся Lа(), причём индекс “а” опускается.

Пример 1. Определить передаточную функцию RС-цепи операторным методом.

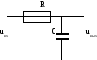
сделав замену T=RC,

найдем

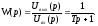
Пример 2. Определить передаточную функцию генератора по его дифференциальному уравнению.

Возьмём преобразование Лапласа от обеих частей уравнения при нулевых начальных условиях

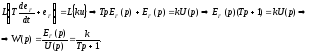
3. Инерционное звено 2-го порядка.

Такие звенья описываются дифференциальным уравнением вида

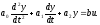Преобразуем по Лапласу это уравнение

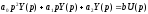или

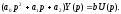
Определим передаточную функцию звена

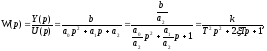
где

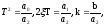
T – постоянная времени, с;

– коэффициент затухания (безразмерная величина);

k – передаточный коэффициент.

В зависимости от величины классифицируются звенья второго порядка по видам:

1. >1 – апериодическое звено II-го порядка.

Характеристическое уравнение звена 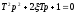имеет корни действительные и отрицательные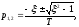данное звено можно представить в виде двух последовательно соединенных звеньев с различными постоянными времени:

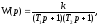тогда при T₁>T₂ переходная функция звена имеет вид

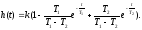
	Корни характ. уравн.	Переходная функция	Амплитудно-фазовая характеристика
1	2	3	4
h t T1+ T2 T2 k + j + i 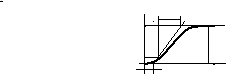>1	действительные, разные, отрицательные

2. =1, 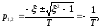оба корня одинаковые и отрицательные.

Можно разложить на два последовательно соединенных апериодических звена с одинаковыми постоянными времени.

1	2	3	4
=1		То же, что и в случае 1.	То же, что и в случае 1.

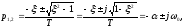3. 0<<1, корни разные, комплексно-сопряженные, с отрицательной вещественной частью; КОЛЕБАТЕЛЬНОЕ ЗВЕНО.

Переходная функция звена имеет вид

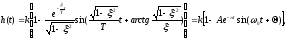
где 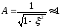при малых ,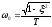- имеет физический смысл собственной частоты колебаний,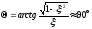при малых .

Период собственных колебаний при малых .

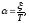
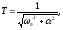
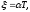
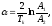
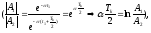
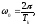
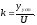
1	2	3	4
+ j + k h t k k 1 u(t) ууст. Tk 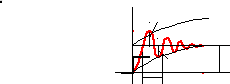0<<1	Корни разные, комплексно-сопряженные, с отрицательной вещественной частью

Чем меньше , тем выше колебательность процесса.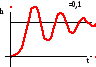

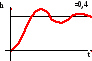
4. =0, 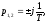такое звено имеет специальное название – КОНСЕРВАТИВНОЕ ЗВЕНО.

Решение дифференциального уравнения имеет вид

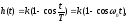где

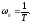
В случаях 1, 2, 3 энергия рассеивалась и колебания затухали, здесь же энергия не рассеивается, а перетекает из одной “емкости” (“емкость” - в универсальном смысле) в другую.

1	2	3	4
k h t + j + k =0	Корни равные, мнимые, комплексно-сопряженные

5. -1<<0,

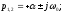
1	2	3	4
+ j + -k h t 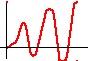-1<<0	Корни комплексно-сопряженные с положительной вещественной частью

Это неустойчивое колебательное звено.

6. <-1

1	2	3	4
<-1	Корни вещественные, разные, положительные		Форма АФХ такая же, как и в случае 5

7. =-1; отличается от случая 6 лишь тем, что корни одинаковые.