Иллюстрация метода на примере решения задачи

“оптимального управления движением поезда”

Следуя по расписанию в t2 оказываемся в В.

Критерий оптимальности – расход электроэнергии или топлива.

Управление – Пк. Надо подобрать такую комбинацию Пк(S), чтобы обеспечить выполнение .

t – должно быть соблюдено по расписанию.

На каждом отрезке считается, что Пк(S) = const и ik(S) = const.

Ось V тоже делим на отрезки. Получаем сетку.

На последнем участке траектории ставим своё управление. Если имеются разные траектории и они попали в один дискрет по скорости, то мы одну из них отбрасываем – ту, которой соответствует min критерия оптимальности, оставляем.

На (N-2)-ом участке, каждой точке, соответствующей концу (N-2)-го участка, соответствуют различные траектории, для которых имеется своё оптимальное управление. Из всего множества траекторий число их в общем случае будем сокращать за счёт попадания в дискрет по скорости, не соответствующего критерию оптимальности.

Рассматривая подобным образом растущее от шага к шагу множество траекторий и исключая нежелательные, мы имеем условно оптимальное управление.

Рассмотрим динамику системы, описываемыми линейными разностными уравнениями вида (1).

(1)

Критерий оптимальности является аддитивным.

(2)

Оптимальное управление должно обеспечивать минимизацию критерия оптимальности (2) на каждом из временных интервалов и оставаясь на каждом отрезке постоянным.

По существу критерий оптимальности является функцией многих переменных.

Рассмотрим построение оптимального управления в последовательности от конца к началу.

N-1 шаг

(3)

В память машины заносим и

N-2 шаг

(4)

С учётом (1) :

(5)

(6)

В память машины (со стиранием предыдущих) записываем :

и

и т.д. …

(7)

Для каждого запоминаем :

и

Все остальные предыдущие можно стереть.

Последний 0-ой шаг

(8)

Получили значения всего критерия оптимальности.

Записываем :

и

Теперь записываем оптимальное управление от начала :

ГРАФ

Траектория оптимального маршрута зависит от начальной точки.

Задача управления взлётом самолёта по критерию минимума затрат горючего.

4. Аналитическое конструирование

оптимальных регуляторов

Динамика системы описывается линейными дифференциальными уравнениями.

мера работ мера работ, выполняемая

самой системы, органами управления,

r > 0

, где

r – весовой коэффициент.

Минимизация критерия в неявной форме не позволяет сделать большим управление.

Метод, изобретенный Лётовым, справедлив для систем, управляемыхинаблюдаемыхи тогда решение существует и единственно и выражается в том, что необходимо решить уравнение Реккати, связанное с нахождением неизвестных коэффициентов закона управления, имеющего вид :

находятся как :

(1)

(2) -уравнение Реккати

- матрица неизвестных коэффициентов

- критерий Сильвестра

Уравнение Реккати в работе Репина и Третьякова было сведено к решению дифференциальных уравнений, которые решаемы на АВМ.

Пример :

,

,

U

Трудность метода : при постановке оптимального регулятора в реальную нелинейную систему необходима проверка, т.к. синтез проводился для линеаризованных систем, а исходная система была нелинейной.

От задачи АКОР в общем случае можно перейти к задаче математического программирования.

5. Методы нелинейного программирования,

как методы решения задач оптимального

управления

При заданной структуре регулятора оптимальное управление, как линейная комбинация фазовых координат. Критерии оптимальности зависят от коэффициентов регулятора - получилась задача нелинейного программирования : нахождение такого сочетания коэффициентов, при которых значения критерия оптимальности будут минимальны. Это и будет являться решением данной задачи.

Найти при ограничениях:

1. параметрических

2. функциональных ,

или

Отыскать такой вектор , который обеспечит минимумQ при ограничениях 1-го и 2-го рода.

Qи φ являются нелинейными функциями, следовательно – задача нелинейного программирования.

Если в задачах линейного программирования существует 1 метод, который может успешно или неуспешно решить задачу (симплекс-метод), то для решения задачи нелинейного программирования существуют десятки, сотни методов решений. Строго формализованной цепочки движения от к Q нет.

Классификация методов НЛП :

1. Детерминированные.

2. Случайные.

1. Нулевого порядка (используют только значения функции)

2. Первого порядка (используют градиенту)

3. Второго порядка (используют 1-ую и 2-ую производную)

0-ой порядок : Q или∆Q

1-ый порядок :Qи

2-ой порядок :Q, и (или)

Q методx

оптимизации

3. Локальные

y

x

x1 x2 x3 x4 x5 x6

точки локального минимума

х3– глобальный минимум

Перебор(сканирование)

1) Х1Х2Q

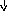
- это количество точек.

В них надо определить критерий оптимальности.

2)

Метод Гаусса-Зейделя

(покоординатный спуск)

Вычисления по этому методу заканчиваются тогда, когда мы окажемся в точке (если ресурс по шагам не исчерпан), из которой движение в любом направлении параллельно координатным осям приводит к возрастанию функции качества.

Вышерассмотренные методы – методы локального поиска.

Для любого шагового метода:

а – рабочий шаг

S– вектор направления поиска

k– номер шага

орты

Для того, чтобы избежать ситуации зацикливания в области экстремума, необходимо предусмотреть процедуру уменьшения шага поиска по мере приближения к точке экстремума.

Градиентный метод

градиент

при поиске минимума мы должны двигаться в сторону антиградиента.

Q

Вычисляем составляющий градиенты в следствие опосредственного влияния параметров Х на целевую функцию Q, составляющую градиента нужно вычислять численным методом.

1. 

( n+1 вычисляемQ(x) )

2. 

( 2nвычисляем )

специальной процедуры для ускоренного продвижения не требуется

Направление движения выбирается, как перпендикуляр к касательной линии уровня.

Достоинство градиентного метода заключается в том, что мы идём в сторону по антиградиенту, сразу к min, но при этом на каждом шаге необходимо делать дополнительные вычисления для определения антиградиента по формулам 1) и 2).

1/

метод градиента не работает в ситуации площадки !

2/

при учёте ограничений на независимые переменные метод градиент так же не работает.

Для устранения ситуации возможно :

либо “ отскок ” от этой границы, либо случайный выбор следующей точки поиска.

Можно идти из т.А в сторону minбольшими шагами (например, через 2 линии уровня).

Метод наискорейшего спуска

Отличается от градиентного тем, что определение направления движения к экстремуму определяется не на каждом шаге (A , B , C , …), а через 3÷5 шагов :

АD G этот метод экономит машинное время, но можно проскочить мимо экстремума.