Обсуждение уравнения Эйлера-Лагранжа

Дифференциальное уравнение Эйлера-Лагранжа – 2-го порядка.

Условия Лежандра: показывают, добились ли мы min или max функционала.

Задача с ограничением типа равенства

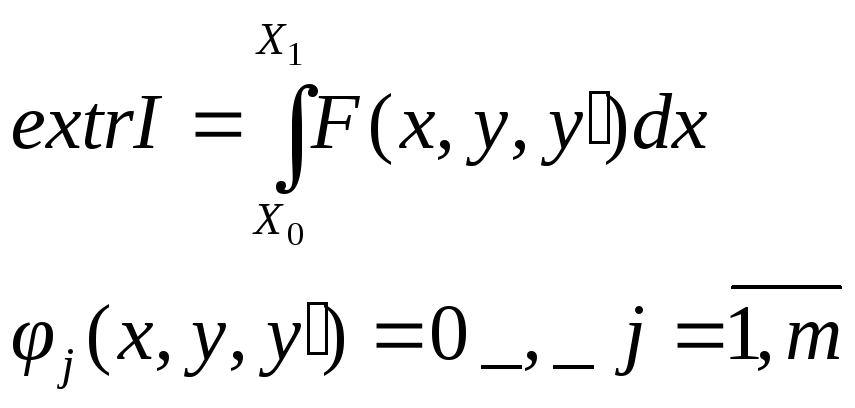
Формируется функция Лагранжа:

,

где - неопределенный множитель Лагранжа.

Изопериметрическая задача

1 2 3 4 5 6

Р = const

Из всех рассмотренных участков надо выбрать один с максимальной площадью.

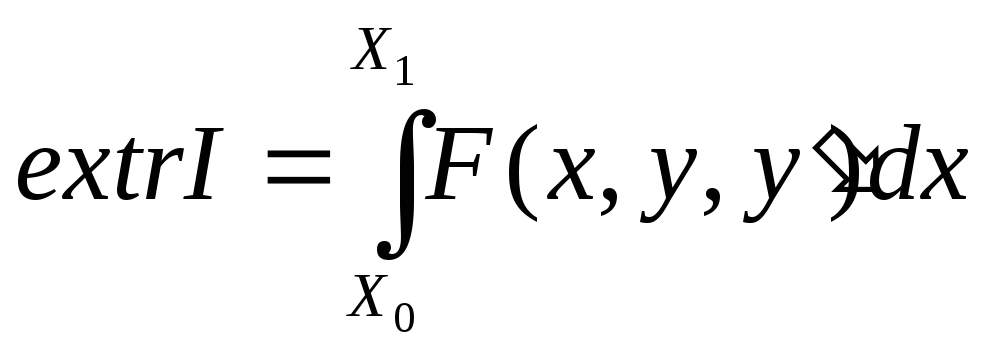(1)

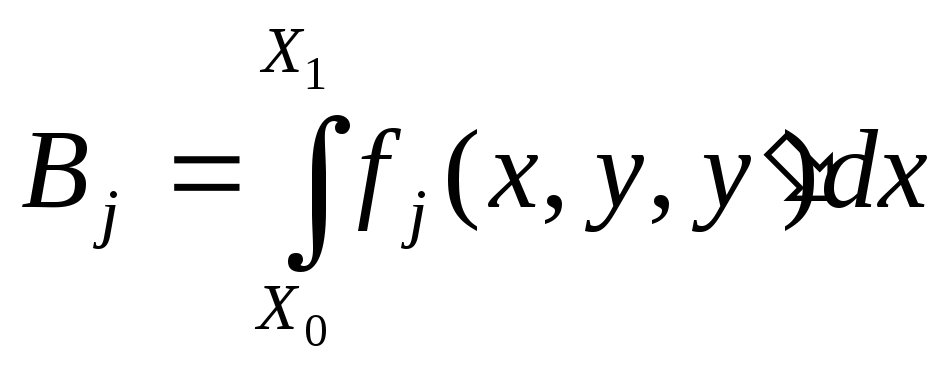(2) - ограничение

Здесь j=1…m

Bj – число

таких ограничений m

Задача : найти (1) при ограничении типа (2).

Образуется функция Лагранжа:

Уравнение Эйлера-Лагранжа: (3)

Неизвестные: y(x) , , j=1…m

Для нахождения неизвестных используем уравнение Эйлера-Лагранжа (3) и m условий изопериметрического вида (2).

Пример: на оптимальную экономичность ( min потерь – задача типа 3 )

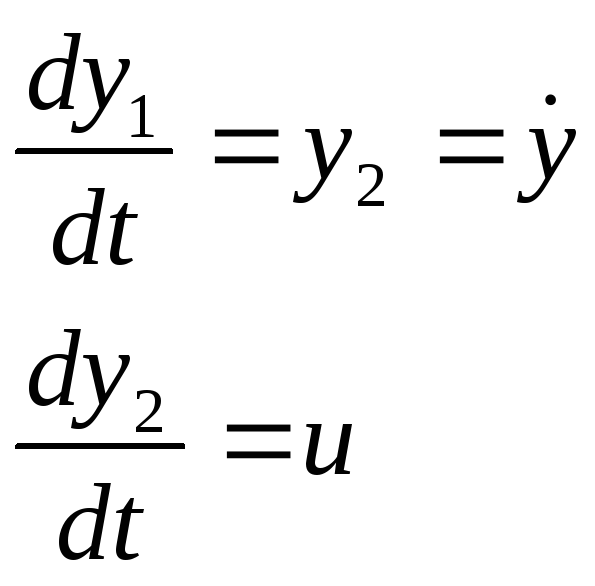
Уравнение Эйлера-Лагранжа:

Неизвестные:

(4)

(5)

Из (4) и (5) получим:

Оптимальное управление имеет вид:

Если взять любое другое

управление, то потери будут

больше.

T/2 T t

-

y*(t)

α0

Возьмем другое управление: u*

a

T/2 T t

-a

y(t)

α0

T/2 T t

Пример: задача типа 1 (на max быстродействие)

Краевые условия:

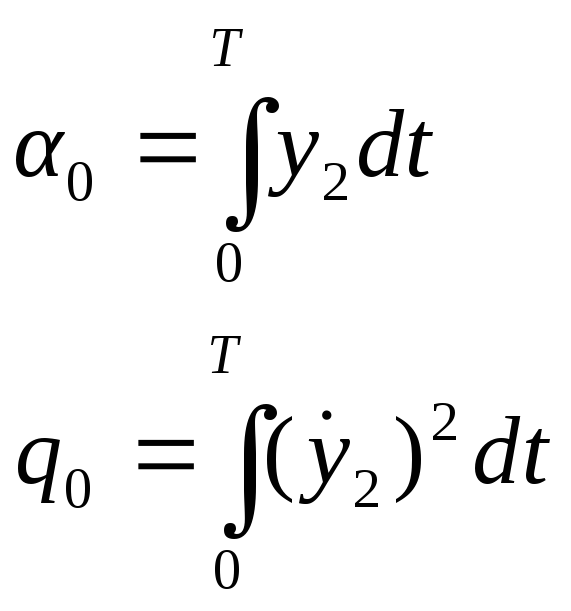
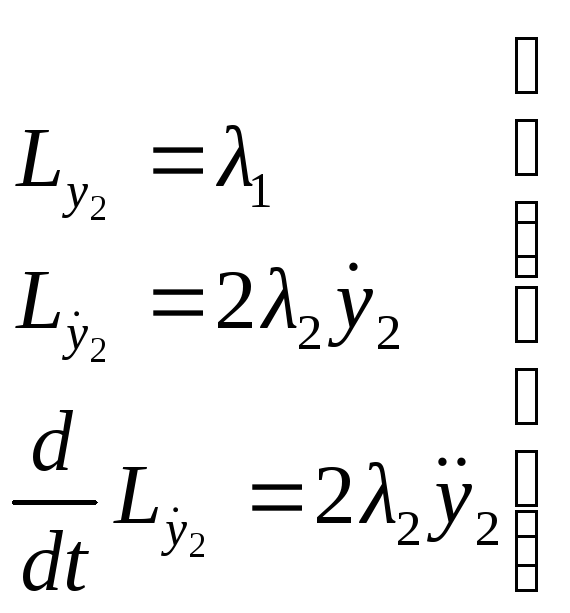
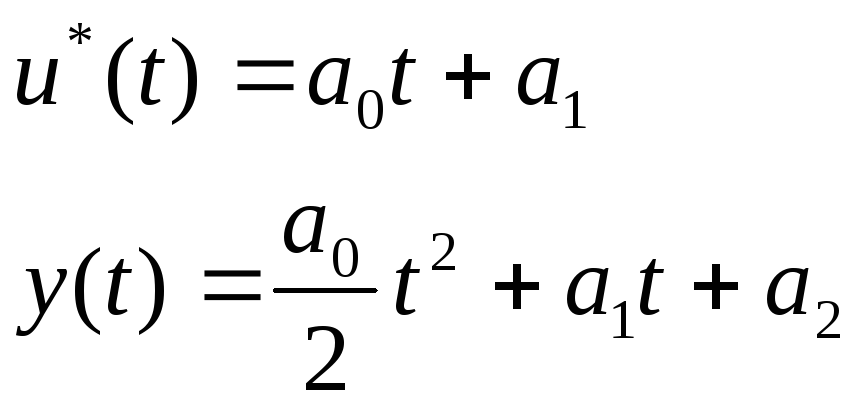
Форма оптимального процесса в этой задаче аналогична предыдущей задаче.

Аналогичный вывод можно сделать и в отношении max производительности (задача 2).

Принцип взаимности

Если в одной задаче один интеграл выступает в качестве экстремизируемого, а другой в качестве изопериметрического ограничения, то решение этой задачи будет соответствовать решению другой задачи, в которой 2-ой функционал выступает в качестве экстремизируемого, а 1-ый в качестве ограничения.

Задача на максимальное быстродействие – это задача с незакрепленными концами. Мы её решили некорректно, поскольку на самом деле правый конец траектории (см. рис.) не закреплен.

Т.е. из всех кривых 1, 2, 3 надо выбрать такую,

чтобы правый конец был бы ближе к нулю.

1 2 3

Т3<T2<T1

T3 T2 T1

Посмотрим, как полученное решение можно применить к схеме управления работой двигателя.

u

τ/2 τ t

-

Найденное оптимальное управление в начальный момент изменяется от 0 до , но в рассматриваемой цепи ( Lя и Rя ) можно добиться максимального приближения, но самого пика не будет ( из-за Lя), т.е. найденное оптимальное решение можно считать приближенным.

Lя - мало Т- постоянная времени – мала.

Кроме того, мы считаем, что магнитный поток (возбуждение) постоянен, т.е. пренебрегали реакцией якоря, чего в больших электрических машинах делать не следует. В них для этого есть демпферная обмотка.

Мы пренебрегли изменением сопротивления якоря в переходном процессе, т.е. в процессе нагрева. А при изменении тока от 0 до max – эта величина Rя может изменяться на 60%.

Кроме того, мы не учли ограничения на управление.

“Вырывание” двигателя из системы управления упростило математическую постановку задачи, но перенесло трудности в техническую часть, поэтому необходимо быть особенно тщательным при постановке задач оптимального управления, создавая адекватную реальному объекту математическую модель и учитывая, по возможности, все ограничения.