Принцип взаимности

Если в одной задаче один интеграл выступает в качестве экстремизируемого, а другой в качестве изопериметрического ограничения, то решение этой задачи будет соответствовать решению другой задачи, в которой 2-ой функционал выступает в качестве экстремизируемого, а 1-ый в качестве ограничения.

Задача на максимальное быстродействие – это задача с незакрепленными концами. Мы её решили некорректно, поскольку на самом деле правый конец траектории (см. рис.) не закреплен.

Т.е. из всех кривых 1, 2, 3 надо выбрать такую,

чтобы правый конец был бы ближе к нулю.

1 2 3

Т3<T2<T1

T3 T2 T1

Посмотрим, как полученное решение можно применить к схеме управления работой двигателя.

u

τ/2 τ t

-

Найденное оптимальное управление в начальный момент изменяется от 0 до , но в рассматриваемой цепи ( Lя и Rя ) можно добиться максимального приближения, но самого пика не будет ( из-за Lя ), т.е. найденное оптимальное решение можно считать приближенным.

Lя - мало Т- постоянная времени – мала.

Кроме того, мы считаем, что магнитный поток (возбуждение) постоянен, т.е. пренебрегали реакцией якоря, чего в больших электрических машинах делать не следует. В них для этого есть демпферная обмотка.

Мы пренебрегли изменением сопротивления якоря в переходном процессе, т.е. в процессе нагрева. А при изменении тока от 0 до max – эта величина Rя может изменяться на 60%.

Кроме того, мы не учли ограничения на управление.

“Вырывание” двигателя из системы управления упростило математическую постановку задачи, но перенесло трудности в техническую часть, поэтому необходимо быть особенно тщательным при постановке задач оптимального управления, создавая адекватную реальному объекту математическую модель и учитывая, по возможности, все ограничения.

Задача с ограничениями типа неравенства

Подрывается основной принцип вариационного исчисления. Двухсторонняя вариация, следовательно уравнение Эйлера-Лагранжа в этом случае не верно. Что делать?

Вводиться специальная функция:

При z=0 имеем границу y(x)=φ(x) .

Уравнение Эйлера-Лагранжа надо записать для вновь введенной переменной:

(2) - для y не годится

Путем подстановок у(х) и у’(x) в вариацию функционала

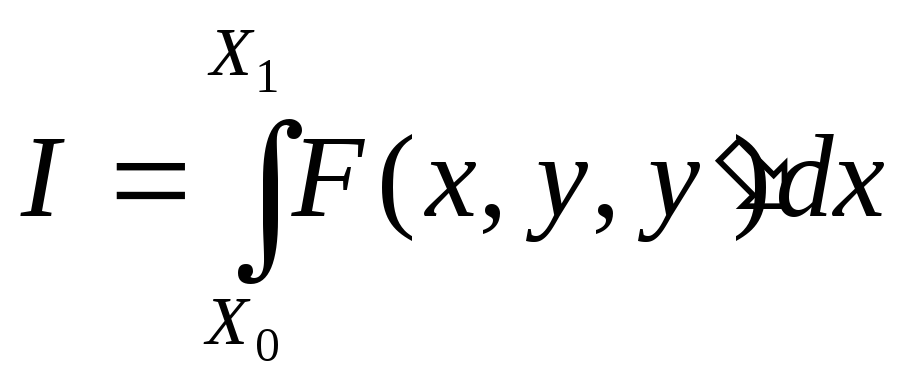(1) и записи уравнения Эйлера-Лагранжа удается получить следующее выражение:

(3)

(4)

1) z=0 (5) либо

2) (6)

Из (5) следует, что у(х)=φ(х)

Вывод: Учет ограничения типа неравенства путем введения специальной функции z (см. выше) позволяет из уравнения Эйлера-Лагранжа, записанного для переменной z (3) для экстремизации функционала (1), получить соотношение (4), которое разлагается на (5) и (6), которые можно охарактеризовать, как:

(5) – мы идем по границе,

(6) – мы идем по экстремали (если бы на у не было наложено ни каких ограничений).

Экстремизация функционала (1) при ограничении на экстремаль получаем следующее решение: - эксремум функционала (1) доставляет сложная составная кривая, состоящая из кусков экстемали (6) и кусков границ (5).

u

+1

t

-1

Пример: обойди болото !!!

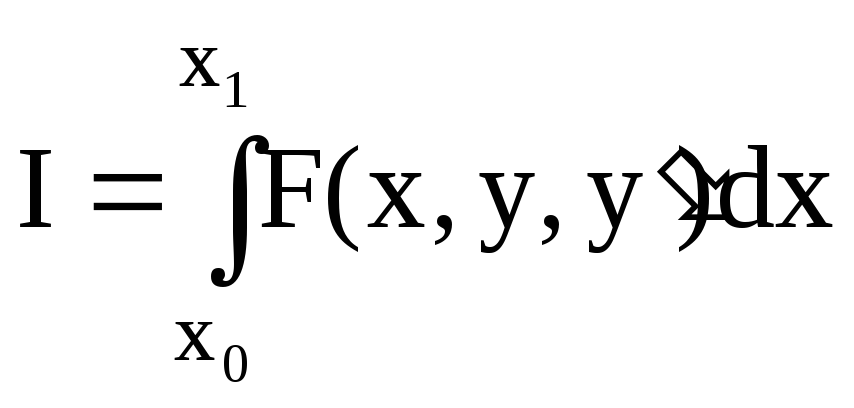
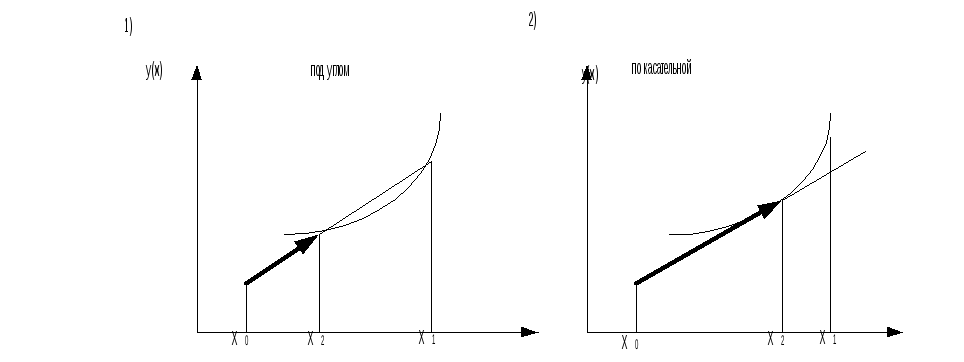
1) если , то по касательной

2) если , то под углом

?

;

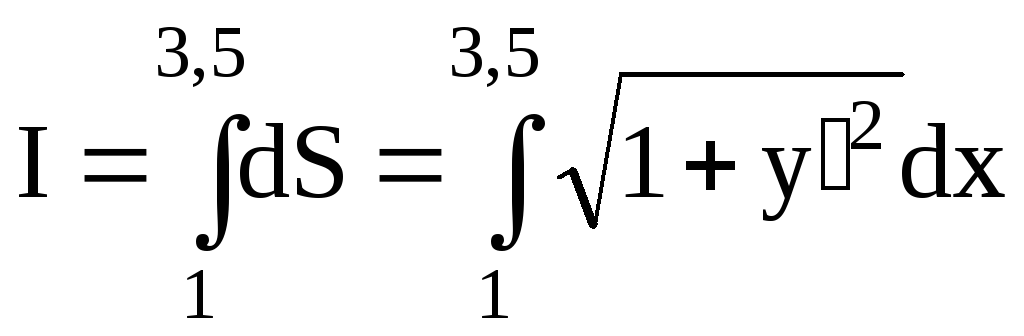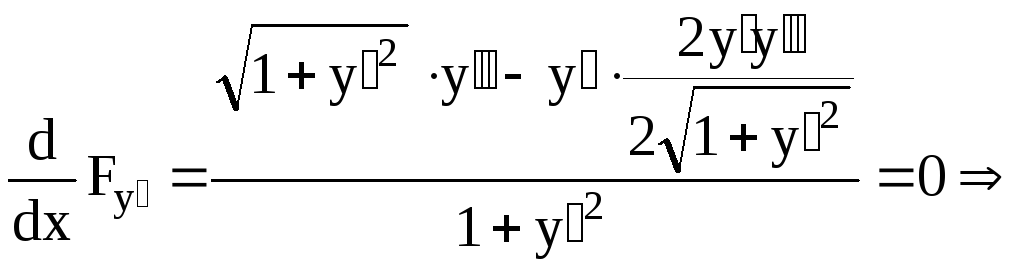
- прямая

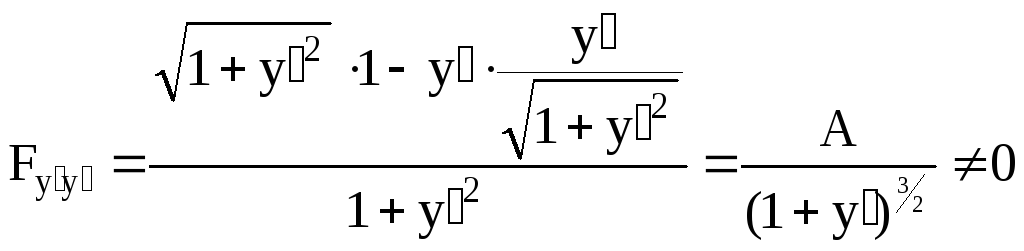
Действительно, при учёте ограничений типа неравенства экстремум достигается на составной прямой, состоящей из участка экстремали и участка границ.

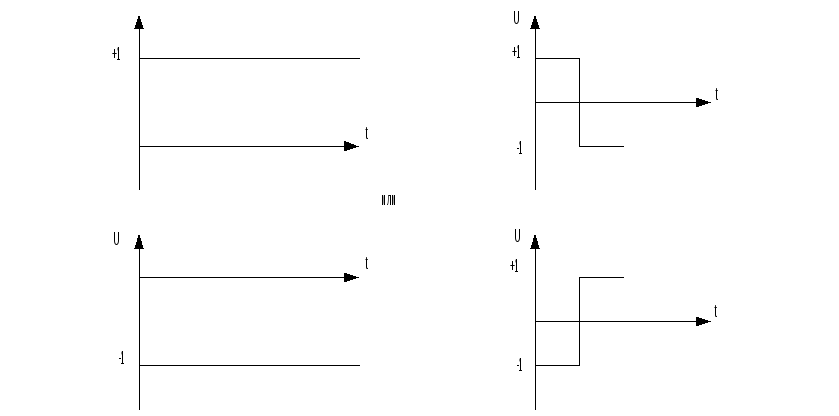
Если заранее известно, что управление имеет кусочно-постоянный характер, то может решить задачу на определение оптимального управления с помощью уравнения Эйлера.(Найти время действия +1 и −1 или найти число переключений)

+1

t0 t1

t

-1

Введение изопериметрического ограничения :

m → ∞

Только в этом случае интеграл

равен Т.

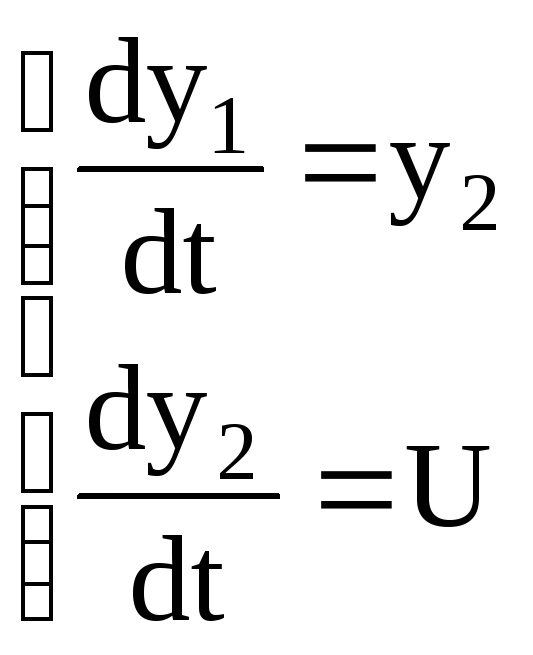- уравнение объекта ;

Функция Лагранжа тогда :

Определить : u(t), y1(t), y2(t)

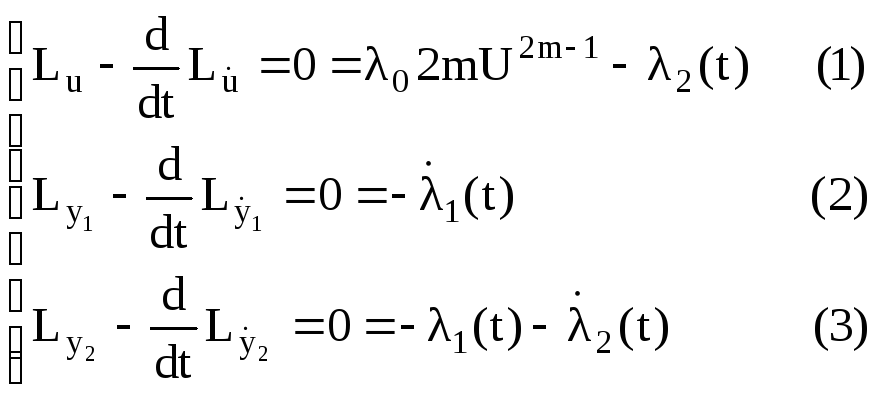
Из математики известно, что

следовательно

Из (2)

Из (3)

Отсюда получаем

Решение данной задачи показывает, что этот метод оказывается затруднительным при решении задач на оптимальное управление.

Имеется ряд задач, где в отличие от вышерассмотренных задач с закреплёнными концами, существуют задачи, где, либо правый конец не закреплён, либо левый, либо оба конца не закреплены.

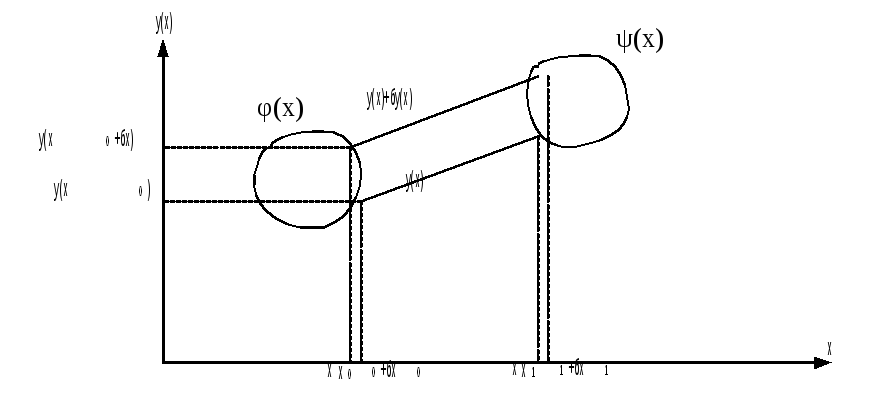Встречаются задачи, где концы будущей экстремали y(x) не закреплены (см. рис.).

Найти

Необходимо получить условия, аналогичные задаче с закреплёнными концами, на основании граничных условий получить уравнение экстремали.

Такие условия называются условиями трансверсальности. Они связывают не сами координаты, а угловые коэффициенты.

!!!

Часто эти условия сводятся к условиям ортогональности.