Синтез оптимального управляющего устройства

U

+1

b t

t₁ t₂

-1

От управления функцией времени переходим к управлению функцией фазовых координат с использованием синтезирующих функций и метода фазовой плоскости.

Задача : управление двигателем с независимым возбуждением

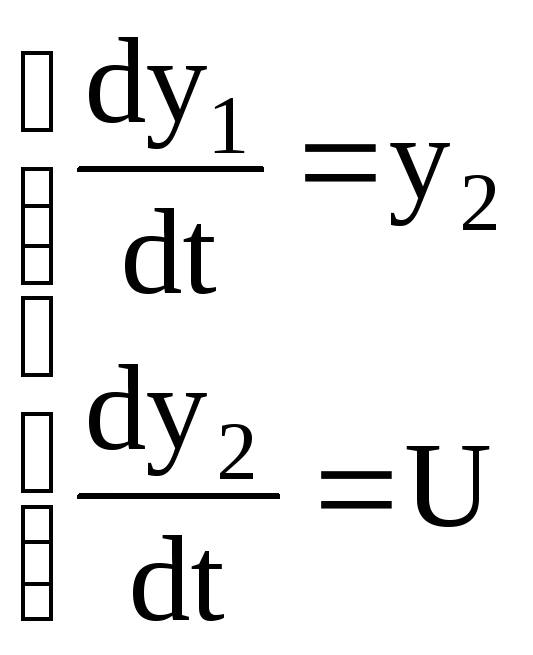(1)

Введём фазовую плоскость с координатами и

Тогда задача оптимального управления может быть сформулирована как задача наибыстрейшего перевода на фазовой плоскости (у₁у₂) из начальной точки в начало координат.

(2) - уравнение объекта

U = +1 U = -1

(3) (4)

Ф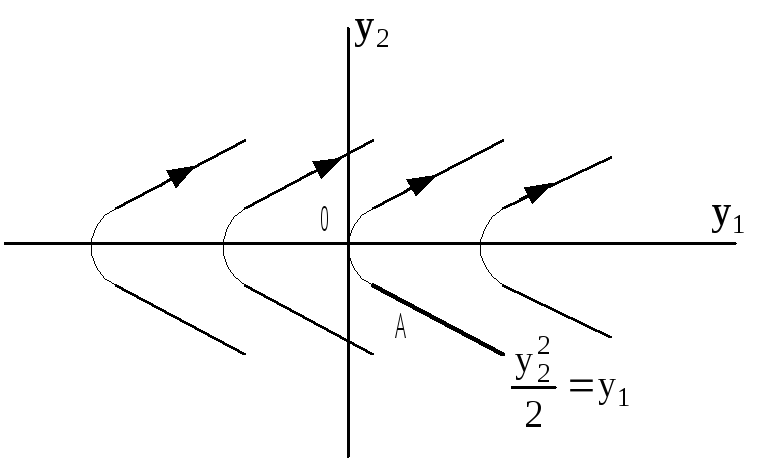азовые траектории :

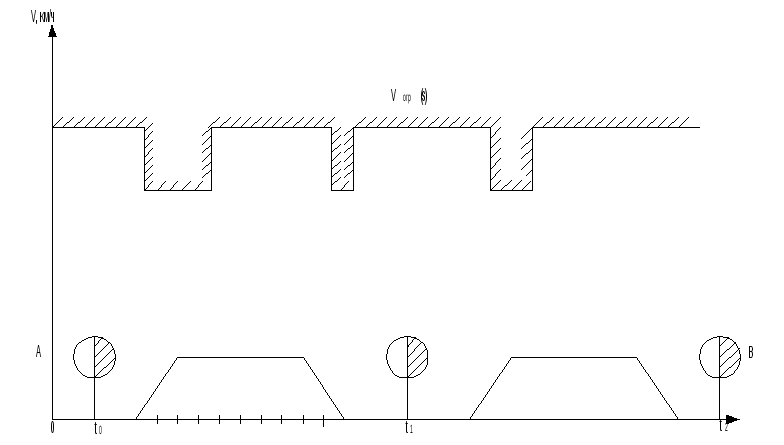
По скольку цель управления – перевод точки из любой точки фазового пространства в начало координат, то заключительный этап движения будет проходить по траекториям АО и ВО, т.о. движение системы на следующем отрезке будет проходить по линии переключения.

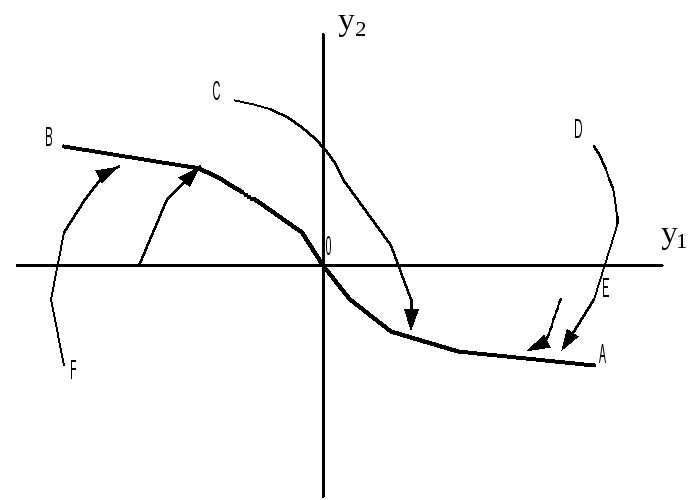
(5) линия переключения АОВ

V = 0 – если находимся на линии переключения

V < 0 - U = -1

V > 0 - U = +1

V – синтезирующая функция, позволяющая перейти от управления функцией времени к управлению функцией фазовых координат.

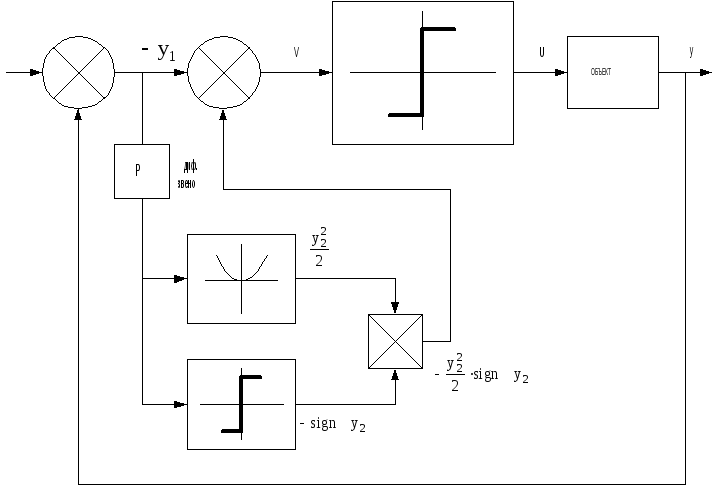Основным недостатком метода является неизвестное значение введённой в гамильтониане ψ-функции.

Управляющее воздействие U₁ … U₂ – подвержено ограничениям типа насыщение. Выбирается так, чтобы иметь максимальным , что даёт,(6)

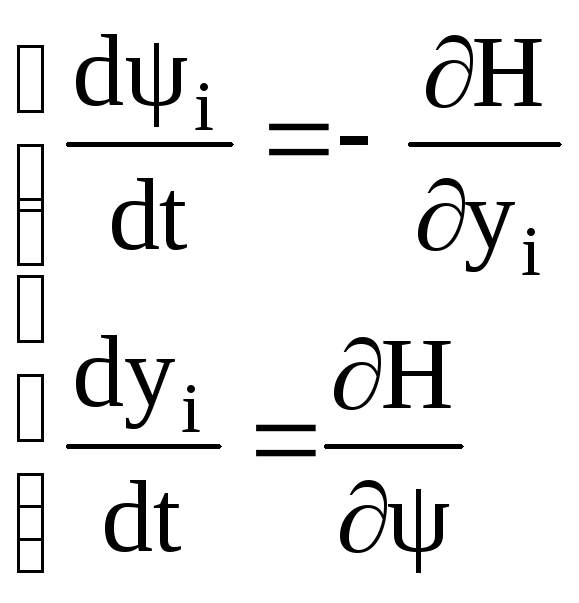(7)

Начальные условия : 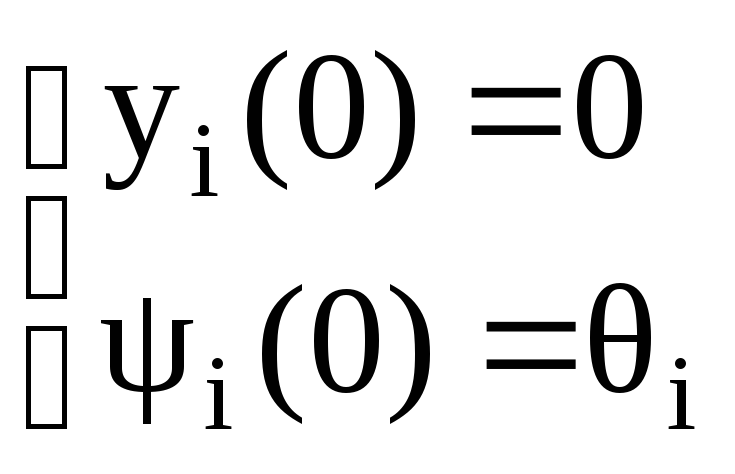(8)

Имея U_i , выбранное согласно (6) уравнения (7) решаем через нач. условия (8).

Это даёт : (9)

(10)

Подставляя (9) и (10) получим :

(11)

Наконец, исключив время t и θ из (11) получим :

- управляющее воздействие, зависящее от фазовых

координат.

Задача синтеза оптимального управления заменяется другой задачей. От (1) до (8) пройти несколько раз, т.е. несколько итераций.

3. Динамическое программирование

( дискретный вариант )

Метод динамического программирования был разработан в 50-ом году нашего столетия Р.Белманом для решения различных задач в области техники, экономики… Метод справедлив для таких систем, для которых справедлив принцип оптимальности.

Оптимальное поведение обладает тем свойством, что какое бы ни было первоначальное состояние и решение в начальный момент времени следующее решение должны составлять оптимальное поведение оптимального состояния, полученного в результате первого решения.

В динамических системах, описываемых дифференциальными уравнениями состояние характеризуется вектором , поведение характеризуется изменениями, а решение соответствует оптимальному управлению. Система, удовлетворяющая принципу оптимальности обладает мартовскими свойствами, т.е. поведение её на конечном отрезке времени полностью определяется управлением на этом отрезкеt₁ ≤ t ≤ t₂ и состояние в момент времени t₁.

Для динамических систем, описанных дифференциальными уравнениями, этот принцип обоснован и доказан, а для остальных систем принимается интуитивно.

Принцип оптимальности ранее применялся к таким системам, математическое описание которых было неизвестно, а состояния, критерий оптимальности которых, задавались экспериментальными значениями в дискретные моменты времени. В этих случаях принцип оптимальности принимался интуитивно.