
- •I Раздел – оптимальные системы.
- •Актуальность курса
- •Постановка задачи оптимального управления Ограничения : − на скорость движения
- •Задача экскаваторщика: управление двигателем постоянного
- •Задача о безударной стыковке двух тел
- •Задача оптимального управления консервативным объектом (задача крановщика)
- •Методы расчёта оптимального управления
- •Обсуждение уравнения Эйлера-Лагранжа
- •Задача с ограничением типа равенства
- •Изопериметрическая задача
- •Принцип взаимности
- •Задача с ограничениями типа неравенства
- •2. Принцип максимума Понтрягина.
- •Теорема принципа максимума Понтрягина
- •Синтез оптимального управляющего устройства
- •3. Динамическое программирование
- •Иллюстрация метода на примере решения задачи
- •Последний 0-ой шаг
- •Случайные методы поиска
2. Принцип максимума Понтрягина.
1. Теорема (см. ниже) будет справедлива для линейных уравнений. Система описывается линейными дифференциальными уравнениями.
![]() (1)
(1)
![]() -
фазовые координаты,
-
фазовые координаты,
![]() -
управляющее воздействие.
-
управляющее воздействие.
Ставиться задача отыскать такое управление U(t), чтобы доставить экстремум функционалуIпри определённых краевых условиях.
U(t) - ?
 (2)
(2)
 ограничение на управление :
ограничение на управление :![]() (3)
(3)
U(t)
![]() Ω
Ω
краевые
условия : ![]() (4)
(4)
Можно
ввести специальные функции ![]()

![]() -
в (1).
-
в (1).
Геометрической интерпретацией является переход от n-мерного пространства к (n+1)-мерному пространству.
Вводится понятие Гамильтониана.
![]() (5)
(5)
![]() -
неизвестная функция времени, для её
определения имеется канонически
сопряженная система уравнений вида :
-
неизвестная функция времени, для её
определения имеется канонически
сопряженная система уравнений вида :
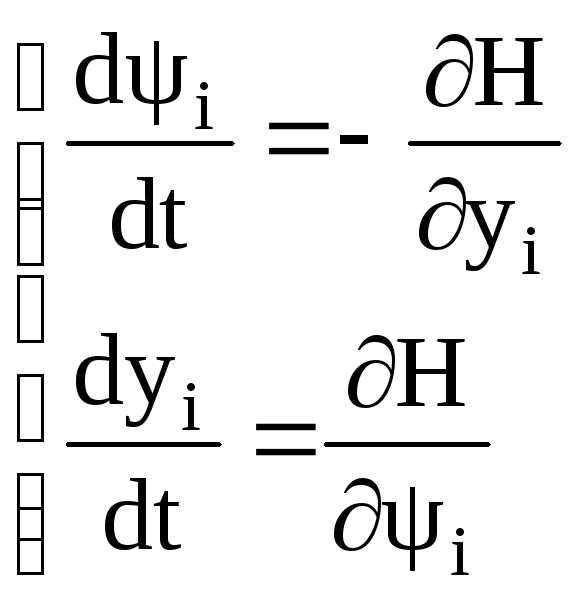 Гамильтонова
система уравнений (6)
Гамильтонова
система уравнений (6)
Теорема принципа максимума Понтрягина
Для
оптимальности управления U(t)
и соответствующее ему в силу уравнений
(1) траектория y(t),
необходимо существование такой ненулевой
непрерывной функции ψ(t)
с координатами ψ1,…ψn
, соответствующее U(t)
и y(t)
в силу уравнений (6), что при любом
t в пределах
t0 ≤ t ≤ T
функция ![]() параметра U
принимает при
параметра U
принимает при ![]() максимальное
значение.
максимальное
значение.
![]()
Для доказательства теоремы принципа максимума Понтрягина используем вариационное исчисление.
 Вычесть значение функционала
неприварьированного и из значния
функционала приварьированного
и приравнять к нулю.
Вычесть значение функционала
неприварьированного и из значния
функционала приварьированного
и приравнять к нулю.
В вариационном исчислении вариации – это непрерывные гладкие функции.
В принципе максимума Понтрягина – скачкообразное изменение управления, которое с самого начала включено в класс отыскиваемых экстремалей. Кусочно-непрерывные функции являются во многих экстремальных задачах оптимальным управлением.
Алгоритм принципа максимума.
Формируется система уравнений объекта
![]()
Формируется гамильтониан Н
![]()
Определяется U, максимизирующее H из системы уравнений
![]() (7)
(7)
Возможно,
что max
Н достигается на границе допустимой
области управления (Ω), тогда для
некоторых j
равенство (7) может не выполняться для
ненулевой, непрерывеой функции ![]() (как
следовало из теоремы принципа max).
(как
следовало из теоремы принципа max).
Для некоторых j max Н достигается на границе U.
Неизвестны
: ![]()
![]()
-----------------------------
(2n+2+r) – штук
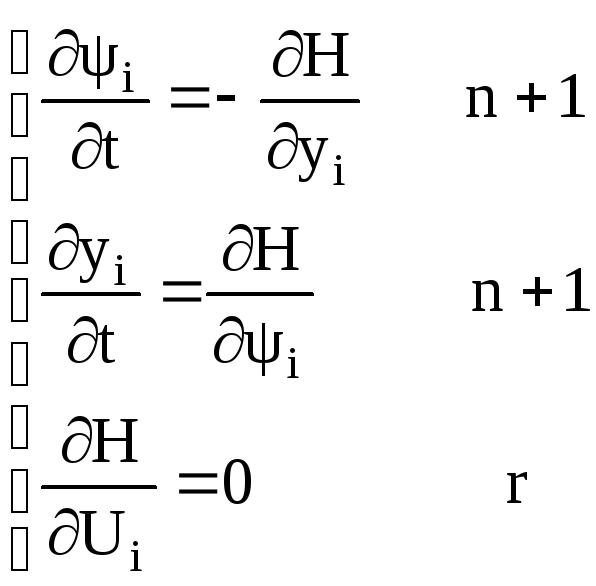 (8)
(8)
В последующих примерах решения совместной системы (8) избежим благодаря низкому порядку n и физическому смыслу задачи.
особенность
принципа максимума
– вариационная задача нахождения
функции ![]() ,
экстремизирующей
i, заменяется
более простой задачей нахождения
параметра
U,
максимизирующей
H.
,
экстремизирующей
i, заменяется
более простой задачей нахождения
параметра
U,
максимизирующей
H.
Пример
: 1.
нахождение с помощью принципа максимума
оптимального управления
двигателем постоянного тока с независимым
возбуждением.![]()
![]()
1)
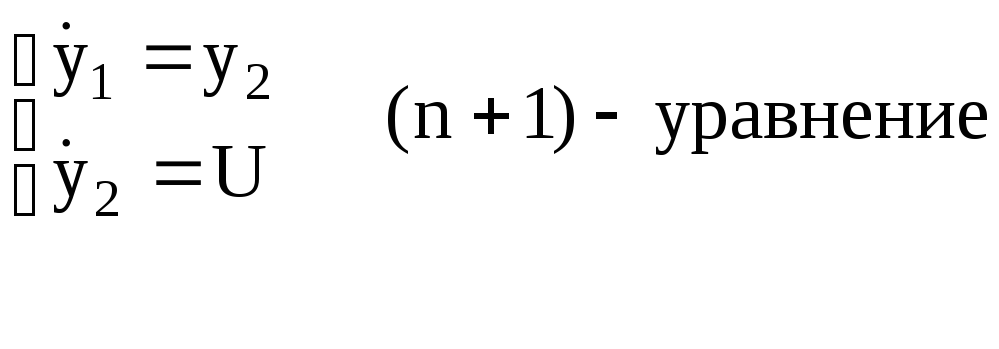

![]()
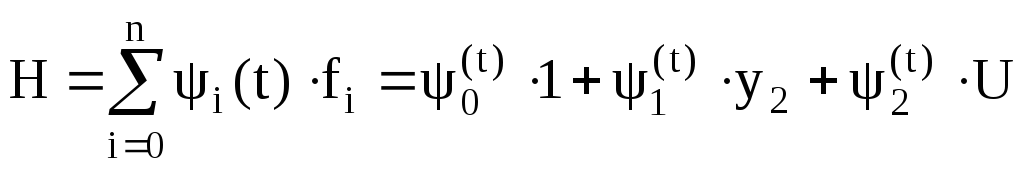
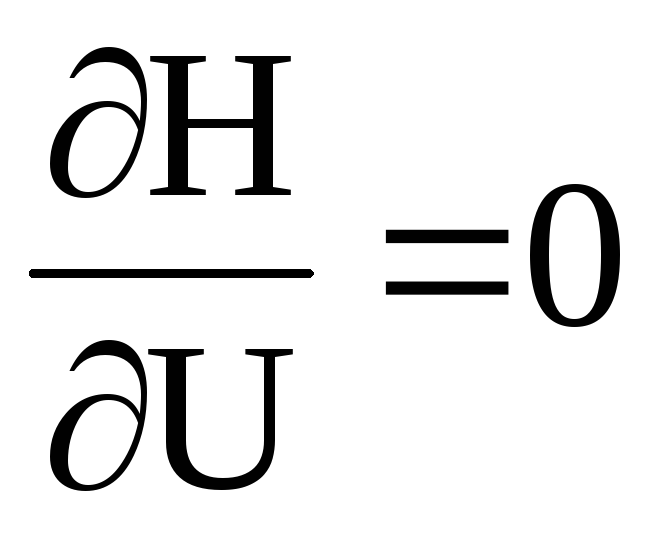
 (9)
(9)
![]() ?
?


![]()
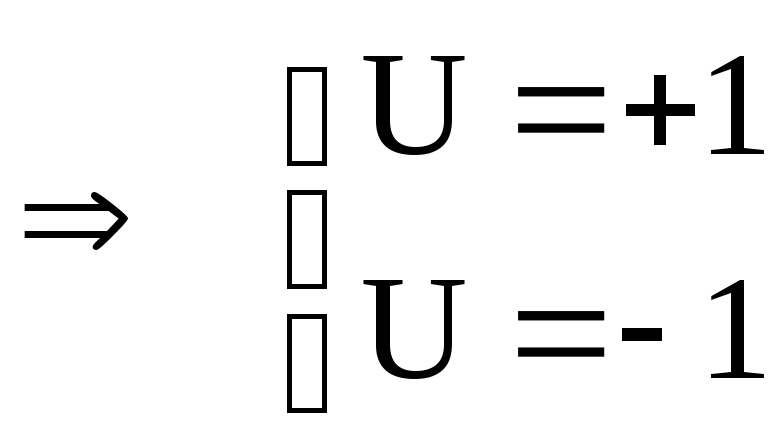
Принцип
максимума Понтрягина требует существования
ненулевой функции. Значит U,
максимизирующее H
следует брать на границе : либо +1, либо
–1. Очевидно, что при ![]() надо
брать U
= +1, а при
надо
брать U
= +1, а при
![]() надо
брать U
= –1.
надо
брать U
= –1.
Этот закон можно записать в виде выражения (9) :
![]() ;
;
![]() ;
;![]()
![]()
![]()
![]()
![]()

Пример : 2 задача о безударной стыковке (оптимальная встреча 2-ух объектов)
![]() (1)
(1)
![]()
![]()

![]()

 (мишень)
(мишень)
![]()


 ya
ya


 -a
-a
![]()
а yb

 (объект)
-b
(объект)
-b
τ
Ставится задача так изменить U(t), чтобы за минимальное время положение и скорости объектов A и B в пространстве совпали.
![]()
2.
![]()
![]()
В
задачах о максимальном
быстродействии
можно опустить в гамильтониане Н первое
слагаемое, равное
![]() .
.
![]() ,
,
![]()



 U
максимизирующее Н :
U
максимизирующее Н : ![]()
![]()
![]()

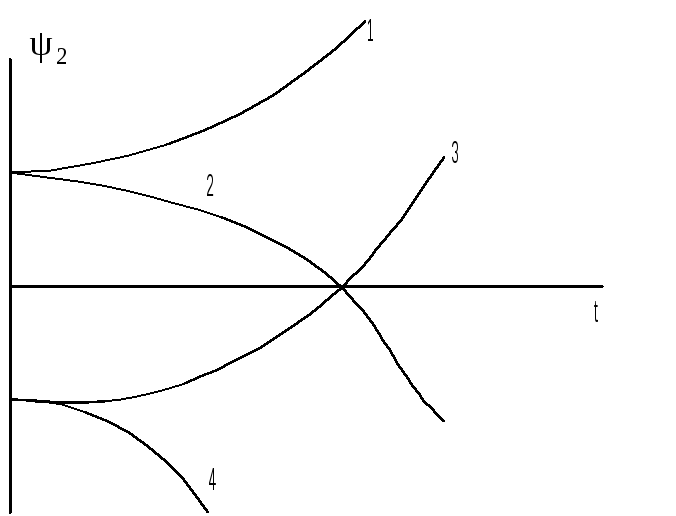
![]() меняет
знак не более одного раза, следовательно
оптимальное управление меняет знак не
более одного раза или имеет не более
двух интервалов постоянства.
меняет
знак не более одного раза, следовательно
оптимальное управление меняет знак не
более одного раза или имеет не более
двух интервалов постоянства.
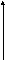 U
U





 +1
b
+1
b

t1=τ1 τ2=t2 t
 -1
-1
Из физического смысла задачи ясно, что в начальный момент управление должно обеспечивать разгон объекта B, а затем его торможение (см. рис.). В момент перехода с тяги не торможение – t1; в момент сближения – τ2=t2, после которого движение должно проходить одинаково и при этом U=b.
Введём
относительное время регулирования
![]()
![]()
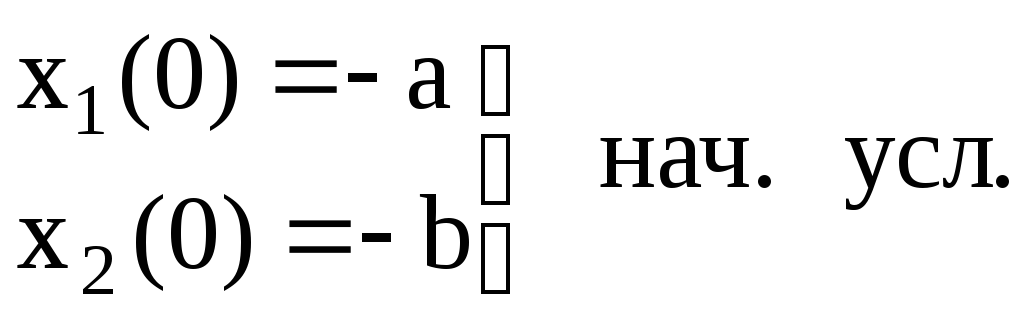
 конечн.
усл.
конечн.
усл.
а) [0 ; τ1]
![]()
![]()
![]() (2)
(2)
![]()
![]() (3)
(3)
![]()
![]() (4)
(4)
н.у.
![]() (6)
(6)
![]()
б)
![]()
![]()
![]() (5)
(5)
интегрируя (5) с учётом н.у. (6) получим :
![]() (7)
(7)
![]() (8)
(8)
По
условию задачи в момент окончания
процесса
![]() .
Если в (7) и (8) подставить
.
Если в (7) и (8) подставить![]() и приравнять к нулю, то получим сложные
функции, содержащие
и приравнять к нулю, то получим сложные
функции, содержащие![]() и
и![]() .
.
![]() (9)
(9)
![]() (10)
(10)
Эти выражения решаются графически :
из
(9) : ![]()
из
(10) : ![]()

Теорема об n интервалах (Фельдбаум А.А.)
Для
линейной системы
n-го порядка,
у которой все корни характеристического
уравнения действительны, а на управление
наложено ограничение
![]() оптимальное управление, доставляющее
экстремум линейному функционалу,
представляющему собой кусочно-постоянную
функцию, принимающую граничные значения
оптимальное управление, доставляющее
экстремум линейному функционалу,
представляющему собой кусочно-постоянную
функцию, принимающую граничные значения![]() и имеющую не более
n интервалов постоянства. (1949г. Фельдбаум
А.А.)
и имеющую не более
n интервалов постоянства. (1949г. Фельдбаум
А.А.)
Пример 3 : Оптимальное управление консервативным объектом
1.
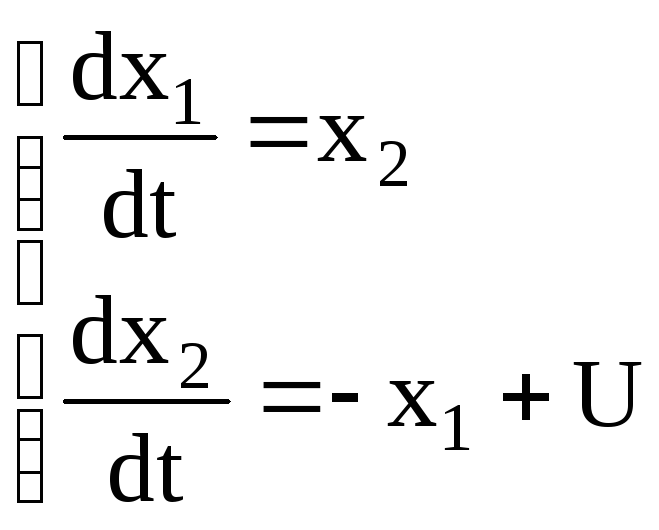 (1)
(1)
![]() -
консервативный объект
-
консервативный объект
корни : p = ±j
![]()
2.
![]() (2)
(2)
![]()
![]()
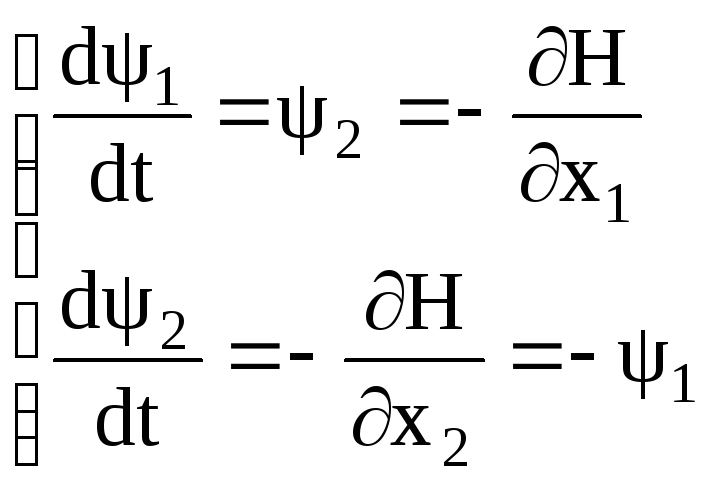 (3)
(3)
![]()
![]()
 U
U







 +1
+1
 t0
t1
t2
t3
t
t0
t1
t2
t3
t


 -1
-1
Для изучения кусков траекторий соответствующих отрезкам времени, на которых либо +1 U, либо –1 U, рассмотрим вспомогательную систему :
![]() (4)
,
(4)
,
отличающуюся от (1) тем, что U=0.
Если построить фазовые траектории для системы (4), то получим :
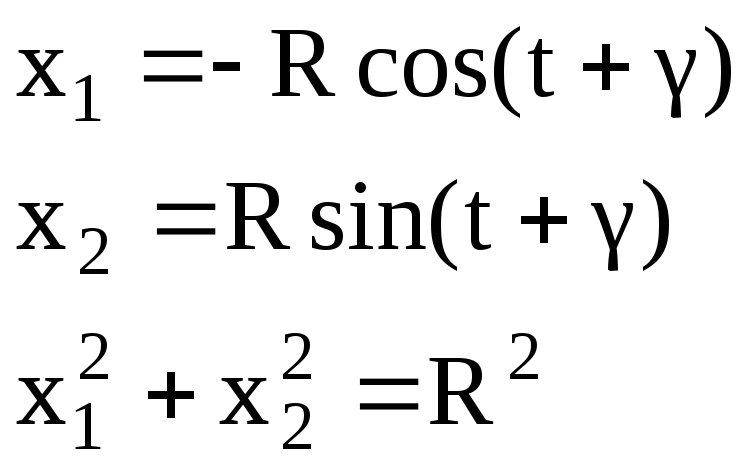
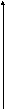 x2
x2



x1



R
Движение по физической траектории по часовой стрелке, движение осуществляется равномерно, с линейной скоростью 2πR (один оборот за время 2π, половина за π).
![]()
![]()
![]()
![]()





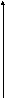 x2
x2
x2
x2








0+1
x1
0-1 x1
Зададимся каким-то видом управления :

 U0
β<π
U0
β<π






 t0
t1
t
t0
t1
t



 π+α
2π+α
π+α
2π+α


α<π

р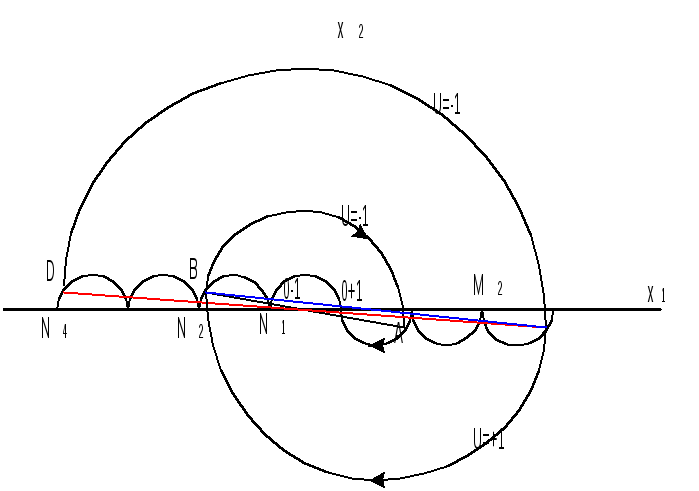 ис.1
ис.1
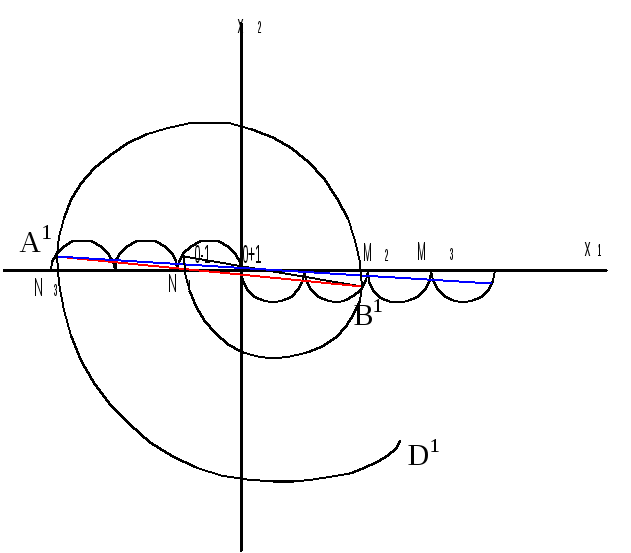
Заключим отрезки оптимальной траектории соответствующего угла ОА при U=+1 и действующем при отрезке β<π.
В т.А фазовая точка, двигаясь в течение отрезка π, попала под действие управления U=–1, т.е. предыдущим для дуги АО является дуга АВ, являющаяся полуокружностью АВ с центром в (0-1) или т.В располагается симметрично точке А на полуокружности N1N2 c центром симметрии (0-1).
Дуге ВА предшествует дуга СВ, соответствующая отрезку времени π, на котором U=+1, т.е. точка С располагается симметрично точке В с центром симметрии на полуокружности М2М3.
Линии переключения: полуокружности радиуса 1
…N4N3N2N1M1M2M3…
Возьмём другое управление:

 U
α<π
U
α<π








 α
α

 t0
π+α 2π+α t1
t
t0
π+α 2π+α t1
t


 β<π
β<π
рис. 2
Объединяя рис.1 и рис.2 получим общий портрет:

Задача с ограничением на фазовые координаты

![]()
 U
U
a







 x2m
x2m
 t
t
t0 I tA II tB III t1
t0 - tA – разгон (тяга), скорость нарастает и достигает x2m в момент tA
tA- tB – управление = 0, режим выбега
tB- t1 – торможение с замедлением -а
II-го участка может не быть
![]()
