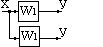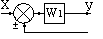- •Введение
- •1. Общая характеристика систем автоматического управления
- •Основные понятия теории автоматического управления
- •1.2. Фундаментальные принципы управления
- •1.3. ОсновНые виды систем автоматического управления
- •2. Математическое описание линейных сау
- •2.1. Статические характеристики
- •2.2. Статическое и астатическое регулирование
- •2.3. Динамические характеристики сау
- •2.4. Передаточная функция сау
- •2.5. Частотные характеристики
- •2.6. Временные характеристики
- •2.7. Элементарные звенья сау
- •2.7.1. Пропорциональное звено
- •2.7.2 Интегрирующее звено
- •2.7.3. Апериодическое или инерционное звено
- •2.7.4. Колебательное звено
- •2.7.5. Дифференцирующее звено
- •2.7.6. Неминимально-фазовые звенья
- •2.8. Структурные схемы сау. Правила преобразования Структурных схем
- •Правила структурных преобразований
- •2.9. Частотные характеристики последовательно соединенных звеньев
- •2.10. Структурные модели сар
- •3. Устойчивость линейных систем автоматического управления
- •3.1. Понятие устойчивости системы.
- •Условие устойчивости сау
- •3.2. Алгебраические критерии устойчивости
- •3.2.1. Необходимое условие устойчивости
- •3.2.2. Критерий Рауса
- •3.2.3. Критерий Гурвица
- •3.3. Частотные критерии устойчивости
- •3.3.1. Принцип аргумента
- •3.3.2. Критерий устойчивости Михайлова
- •3.3.3. Критерий устойчивости Найквиста
- •3.4. Запасы устойчивости по модулю и фазе
- •3.5. Анализ устойчивости по лачх
- •3.6. Метод d-разбиений
Правила структурных преобразований
|
Преобразование |
Структурная схема | |
|
Исходная |
Эквивалентная | |
|
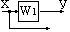
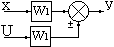
Перенос точки разветвления через элемент |
|
|
|
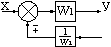
Перенос сумматора через элемент |
|
|
|
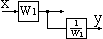
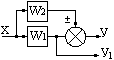
Вынос точки разветвления из параллельного соединения |
|
|
|
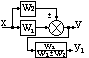
Вынос точки разветвления из контура обратной связи |
|
|
Рассмотрим несколько примеров преобразования структурных схем САУ.
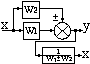
Пример 2.1. Найти передаточную функцию системы по представленной структурной схеме:
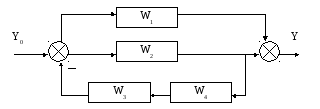
W' = W3·W4 – последовательное соединение двух звеньев:

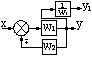
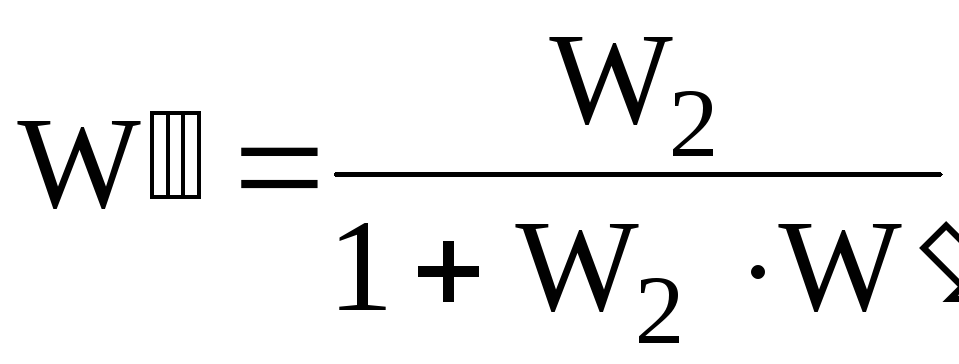 –соединение
звеньев с отрицательной обратной
связью:
–соединение
звеньев с отрицательной обратной
связью:
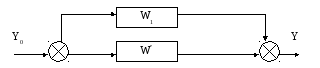
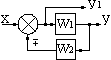
 –параллельное
соединение двух звеньев:
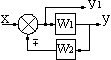
–параллельное
соединение двух звеньев:

Следует, однако, помнить о том, что за относительно простыми соотношениями при получении передаточной функции скрываются передаточные функции типовых звеньев и передаточная функция системы в целом может иметь очень высокий порядок.
Пример 2.2. Рассмотрим схему САР напряжения генератора постоянного тока (рис.2.34).
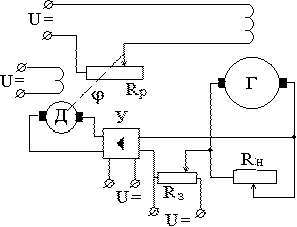
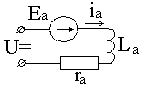
Рис.2.34 Рис.2.35
Выведем дифференциальное уравнение исполнительного двигателя постоянного тока. Его схема замещения изображена на рис.2.35.
Для якорной цепи справедливо уравнение
![]()
Если
принять, что
![]() ,
где φ – угол поворота вала двигателя,
то
,
где φ – угол поворота вала двигателя,
то
![]() ,
,
то есть
![]() ,
,
где
![]() –
постоянная времени якорной цепи;
–
постоянная времени якорной цепи;![]() ,
,![]() – коэффициенты пропорциональности.
– коэффициенты пропорциональности.
Если
учесть, что
![]() ,
где
J
– момент инерции якоря, M
- электромагнитный момент, Мс
– момент сопротивления, то получим
,
где
J
– момент инерции якоря, M
- электромагнитный момент, Мс
– момент сопротивления, то получим
![]()
Следовательно,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Здесь
![]() – электромеханическая постоянная
времени;
– электромеханическая постоянная
времени;
![]()
![]()
![]()
![]() –коэффициенты
пропорциональности;
–коэффициенты
пропорциональности;
![]() –передаточные
функции по напряжению и моменту
сопротивления.
–передаточные
функции по напряжению и моменту
сопротивления.
Структурная схема двигателя постоянного тока показана на рис.2.36.
Аналогичным
образом выводится передаточная функция
генератора постоянного тока, которая
с учетом пренебрежения индуктивностью
обмотки якоря имеет вид, показанный на
рис.2.37, где
![]()
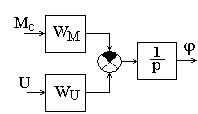
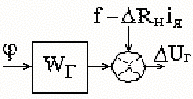
Рис.2.36 Рис.2.37
У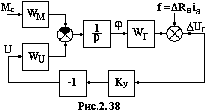 силитель
можно представить пропорциональным
звеном с коэффициентом усиленияKу.
В окончательном виде структурная схема
САР напряжения генератора постоянного
тока показана на рис.2.38.
силитель
можно представить пропорциональным
звеном с коэффициентом усиленияKу.
В окончательном виде структурная схема
САР напряжения генератора постоянного
тока показана на рис.2.38.
2.9. Частотные характеристики последовательно соединенных звеньев
При исследовании и проектировании САУ часто используют АФЧХ, ЛАЧХ и ЛФЧХ разомкнутых систем. Это объясняется тем, что разомкнутые САУ более просто исследовать экспериментально, чем замкнутые. В то же время по ним можно получить исчерпывающую информацию о поведении данной САУ в замкнутом состоянии.
Любую многоконтурную САУ можно привести к одноконтурной. Разомкнутая одноконтурная САУ состоит из цепочки последовательно соединенных динамических звеньев. Зная передаточную функцию разомкнутой САУ можно построить ее ЧХ. И наоборот, зная ЧХ разомкнутой САУ, снятую, например, опытным путем, можно найти ее передаточную функцию.
Передаточная функция разомкнутой одноконтурной системы равна произведению передаточных функций отдельных звеньев (2.22):
![]() .
.
Заменив в этом выражении p на jω получим ее АФЧХ:
![]() . (2.26)
. (2.26)
АЧХ:
![]() . (2.27)
. (2.27)
Тогда логарифмические частотные характеристики определятся так–
ЛАЧХ равна сумме ЛАЧХ звеньев:
![]() , (2.28)
, (2.28)
ЛФЧХ – сумме сдвигов фаз звеньев:
![]() . (2.29)
. (2.29)
Таким образом ЛАЧХ и ЛФЧХ разомкнутой САУ строят путем графического сложения ЛАЧХ и ЛФЧХ звеньев. При этом ограничиваются построением асимптотической ЛАЧХ.
Для построения ЛАЧХ и ЛФЧХ рекомендуется следующий порядок:
1) раскладывают сложную передаточную функцию на множители, являющиеся передаточными функциями типовых динамических звеньев (порядок полиномов числителя и знаменателя не выше второго);
2) вычисляют сопрягающие частоты отдельных звеньев и строят асимптотические ЛАЧХ и ЛФЧХ каждого элементарного звена;
3) путем графического суммирования ЛАЧХ и ЛФЧХ звеньев строят результирующие ЧХ.
Рассмотрим конкретный пример:
![]() =
W1W2W3W4.
=
W1W2W3W4.
Раскладываем данную передаточную функцию на передаточные функции элементарных звеньев:
1) безынерционное звено:
W1 = K1 = 100 => L(ω) = 20lg100 = 40;
2) форсирующее звено:
W2 = p + 1;
его параметры: K2 = 1, T2 = 1, ω2 = 1/T2 = 1;
3) интегрирующее звено:
W3 = 1/p;
его ЛАЧХ проходит через точку L = 0 при частоте ω= 1;
4) апериодическое звено:
W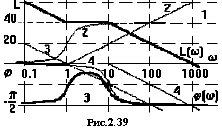 4
= 1/(0,1p + 1);
4
= 1/(0,1p + 1);
его параметры: K4 = 1, T4 = 0,1, ω4 = 1/T4 = 10.
Порядок построения ЛАЧХ и ЛФЧХ показан на рис.2.39.
Иногда требуется решить обратную задачу, то есть определить передаточную функцию по известной ЛАЧХ. Процедура определения передаточной функции состоит из следующих этапов:
1) известная ЛАЧХ представляется в асимптотическом виде, для этого непрерывная кривая заменяется отрезками прямых либо горизонтальных, либо с наклоном, кратным ±20 дб/дек;
2) асимптотическая ЛАЧХ раскладывается на ЛАЧХ элементарных звеньев;
3) для каждой из полученных ЛАЧХ определяются k и ω1 = 1/T и записывается передаточная функция типового звена;
4) передаточная функция САУ определяем путем перемножения передаточных функций типовых звеньев.
О писанный
порядок иллюстрируется на рис.2.40.
писанный
порядок иллюстрируется на рис.2.40.
Здесь ЛАЧХ может быть представлена суммой ЛАЧХ четырех типовых звеньев: пропорционального W1 = 100, апериодического W2 = 1/(p + 1), форсирующего W3 = 0.1p + 1 и апериодического W4 = 1/(0.01p + 1).
Таким образом, передаточная функция разомкнутой САУ имеет вид:
![]()
В более сложных случаях наклоны ЛАЧХ на некоторых участках превышают ± 20 дб/дек. Тогда помимо параметров K и T приходится определять еще и коэффициенты демпфирования r.
Зная передаточную функцию разомкнутой САУ можно построить ее уравнение динамики:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким образом, можно определить уравнение динамики реальных звеньев и всей реальной САУ, если оно теоретически это сделать затруднительно. Для снятия частотных характеристик реальной разомкнутой САУ на ее вход подают гармонический сигнал с изменяемой частотой и определяют изменение амплитуды и фазы выходного сигнала в зависимости от частоты. По полученным характеристикам определяют уравнение динамики, после чего САУ можно исследовать теоретически.