
- •Тема 8. Линейные операторы в евклидовых и в унитарных пространствах.
- •1. Сопряженные операторы.
- •2. Самосопряженные операторы.
- •3. Нормальные операторы.
- •4. Унитарные операторы.
- •5. Ортогональные операторы.
- •Тема 9. Линейные, билинейные и квадратичные формы.
- •1. Линейные формы.
- •2. Билинейные формы.
- •3. Квадратичные формы.
- •4. Методы приведения квадратичной формы к каноническому виду.
3. Квадратичные формы.
Пусть
![]() – симметричная билинейная форма,
определенная на линейном пространстве
– симметричная билинейная форма,
определенная на линейном пространстве
![]() .
.
![]() называют квадратичной формой,
определенной на
называют квадратичной формой,
определенной на
![]() .
.
Замечание.
Мы потребовали
![]() .
Это объясняется следующими соображениями.
Если взять произвольную билинейную
форму
.
Это объясняется следующими соображениями.
Если взять произвольную билинейную
форму
![]() ,
то выражение
,
то выражение
![]() будет симметричной билинейной
формой. Положим в нем
будет симметричной билинейной
формой. Положим в нем
![]() ,
тогда получим
,
тогда получим
![]() ,
т.е. то же самое, как если бы в исходной
форме
,
т.е. то же самое, как если бы в исходной
форме
![]() мы положили
мы положили
![]() .
.
Пример.
![]()
![]() ,
,
![]() – заданная действительная матрица,
– заданная действительная матрица,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
Квадратичная форма
.
Квадратичная форма
![]()
![]()
![]() .
Для изучения квадратичной формы матрицу
.
Для изучения квадратичной формы матрицу
![]() можно считать симметричной – этого
всегда можно добиться следующей
группировкой слагаемых:
можно считать симметричной – этого
всегда можно добиться следующей
группировкой слагаемых:
![]() .
Если в
.
Если в
![]() введено скалярное произведение
введено скалярное произведение
![]() ,
то рассматриваемая квадратичная форма
имеет вид
,
то рассматриваемая квадратичная форма
имеет вид
![]()
![]() ,
где
,
где
![]() .
.
Исходную
симметричную билинейную форму
![]() называют полярной для квадратичной
формы
называют полярной для квадратичной
формы
![]() .
Матрицей квадратичной формы, определенной
на конечномерном линейном пространстве,
называют матрицу ее полярной билинейной
формы.
.
Матрицей квадратичной формы, определенной
на конечномерном линейном пространстве,
называют матрицу ее полярной билинейной
формы.
Теорема 7. Полярная билинейная форма однозначно определяется своей квадратичной формой.
Доказательство.
Пусть
![]() – квадратичная форма, где симметричная
билинейная форма
– квадратичная форма, где симметричная
билинейная форма
![]() нам неизвестна; найдем её. По свойствам
билинейной формы и в силу ее симметричности
имеем
нам неизвестна; найдем её. По свойствам
билинейной формы и в силу ее симметричности
имеем
![]()
![]() .
Отсюда
.
Отсюда
![]() .
.
Доказанная теорема служит еще одним обоснованием того, что при изучении квадратичных форм достаточно рассматривать только симметричные билинейные формы.
Пример.
![]()
![]() .
Положим
.
Положим
![]() для любой непрерывной на
для любой непрерывной на
![]() функции
функции
![]() .
Билинейная форма, полярная к квадратичной
форме
.
Билинейная форма, полярная к квадратичной
форме
![]() ,
имеет вид
,
имеет вид
![]()
![]() .
.
Всюду далее мы будем рассматривать
только действительные конечномерные
линейные пространства
![]() ,
,
![]() .
Пусть
.
Пусть
![]() и
и
![]() – два базиса в
– два базиса в
![]() ,
,
![]() ,
,
![]()
![]() и
и
![]()
![]() – координаты элемента
– координаты элемента
![]()
![]() в этих базисах:
в этих базисах:
![]() ,
,
![]() .
Тогда
.
Тогда
![]() (см. тему 2). Определенная на
(см. тему 2). Определенная на
![]() квадратичная форма
квадратичная форма
![]() в базисе
в базисе
![]() задается при помощи действительной
симметричной
задается при помощи действительной
симметричной
![]() -матрицы
-матрицы
![]() :
:
![]() .
.
![]() можно рассматривать как функцию
можно рассматривать как функцию
![]() независимых действительных переменных
независимых действительных переменных
![]() – однородный многочлен степени 2
от этих переменных. В базисе
– однородный многочлен степени 2
от этих переменных. В базисе
![]() та же квадратичная форма
та же квадратичная форма
![]() является функцией независимых
действительных переменных
является функцией независимых
действительных переменных
![]() и задается при помощи действительной
симметричной матрицы
и задается при помощи действительной
симметричной матрицы
![]() :
:
![]() (см. теорему 4). Основная задача, связанная
с изучением заданной в базисе
(см. теорему 4). Основная задача, связанная
с изучением заданной в базисе
![]() квадратичной формы
квадратичной формы
![]() ,
состоит в нахождении такого базиса
,
состоит в нахождении такого базиса
![]() (или, что то же самое, – таких переменных
(или, что то же самое, – таких переменных
![]() ),
что
),
что
![]() имеет в переменных
имеет в переменных
![]() наиболее простой вид.
наиболее простой вид.
Рассмотрим
сначала случай, когда
![]() – евклидово пространство и
– евклидово пространство и
![]() – ортонормированный базис. По
теореме 21 темы 8 всякая действительная
симметричная матрица
– ортонормированный базис. По
теореме 21 темы 8 всякая действительная
симметричная матрица
![]() ортогонально подобна действительной
диагональной матрице
ортогонально подобна действительной
диагональной матрице
![]() :
:
![]() ,
где
,
где
 ,
,
![]() – собственные значения матрицы
– собственные значения матрицы
![]() ,
а
,
а
![]() – ортогональная матрица, т.е.
– ортогональная матрица, т.е.
![]() .
Поэтому, если в качестве новых независимых
переменных выбрать
.
Поэтому, если в качестве новых независимых
переменных выбрать
![]()
![]() ,
то получим
,
то получим
![]()
![]() .
.
Определение. Вид квадратичной формы с диагональной матрицей называют ее каноническим видом.
Мы только что обнаружили важный факт:
Теорема 8. Всякая квадратичная форма, определенная на действительном евклидовом пространстве, может быть приведена к каноническому виду при помощи линейной замены независимых переменных с ортогональной матрицей преобразования этих переменных.
Очевидно, что
базис
![]() евклидова пространства
евклидова пространства
![]() ,
в котором квадратичная форма имеет
указанный в теореме 8 канонический вид,
является ортонормированным базисом,
состоящим из собственных векторов
матрицы квадратичной формы. Операция
построения ортонормированного
базиса, в котором квадратичная форма
имеет канонический вид, называется
приведением ее к главным осям.
Вообще, привести квадратичную форму
,
в котором квадратичная форма имеет
указанный в теореме 8 канонический вид,
является ортонормированным базисом,
состоящим из собственных векторов
матрицы квадратичной формы. Операция
построения ортонормированного
базиса, в котором квадратичная форма
имеет канонический вид, называется
приведением ее к главным осям.
Вообще, привести квадратичную форму
![]() к каноническому виду – значит найти
переменные
к каноническому виду – значит найти
переменные
![]() и выражение
и выражение
![]() ,
содержащее только квадраты этих
переменных. Если приведение к каноническому
виду производится при помощи ортогонального
преобразования, то для записи этого
канонического вида
,
содержащее только квадраты этих
переменных. Если приведение к каноническому
виду производится при помощи ортогонального
преобразования, то для записи этого
канонического вида
![]() достаточно найти собственные значения
матрицы
достаточно найти собственные значения
матрицы
![]() .
Но чтобы найти переменные, в которых
построен этот канонический вид, надо
знать и собственные векторы матрицы
.
Но чтобы найти переменные, в которых
построен этот канонический вид, надо
знать и собственные векторы матрицы
![]() .
Действительно, условие
.
Действительно, условие
![]() означает, что
означает, что
![]() ,
или поэлементно:
,
или поэлементно:
![]() .
Следовательно,
.
Следовательно,
![]() -ый
столбец матрицы
-ый
столбец матрицы
![]() состоит из координат собственного
вектора матрицы
состоит из координат собственного
вектора матрицы
![]() ,
отвечающего собственному значению
,
отвечающего собственному значению
![]() ,
,
![]() .
Напомним, что столбцы ортогональной
матрицы
.
Напомним, что столбцы ортогональной
матрицы
![]() образуют ортонормированную систему в
смысле скалярного произведения
образуют ортонормированную систему в
смысле скалярного произведения
![]() в
в
![]() .
Полученный в теореме 8 результат является
выражением следующего факта:
.
Полученный в теореме 8 результат является
выражением следующего факта:
Утверждение.
Для любой квадратичной формы
![]() ,
определенной на евклидовом пространстве
,
определенной на евклидовом пространстве
![]() ,
существует единственный самосопряженный
оператор
,
существует единственный самосопряженный
оператор
![]()
![]()
![]()
![]() такой, что
такой, что
![]()
![]() для любого
для любого
![]()
![]() .
.
(Докажите самостоятельно.)
Ортогональное
преобразование переменных
![]() определено только в евклидовом
пространстве, и оно дает лишь один из
канонических видов квадратичной формы.
Канонический вид квадратичной формы
не является однозначно определенным.
Если в некотором базисе линейного (не
обязательно евклидова) пространства
определено только в евклидовом
пространстве, и оно дает лишь один из
канонических видов квадратичной формы.
Канонический вид квадратичной формы
не является однозначно определенным.
Если в некотором базисе линейного (не
обязательно евклидова) пространства
![]() квадратичная форма
квадратичная форма
![]() имеет канонический вид, то переставляя
элементы этого базиса (т.е. производя
перенумерацию независимых переменных),
снова получим
имеет канонический вид, то переставляя
элементы этого базиса (т.е. производя
перенумерацию независимых переменных),
снова получим
![]() в каноническом виде. Если
в каноническом виде. Если
![]()
![]()
![]() ,
то полагая
,
то полагая
![]() ,
где все коэффициенты
,
где все коэффициенты
![]() ,
получим другой канонический вид
,
получим другой канонический вид
![]()
![]() .
.
Пример.
Пусть
![]()
![]()
![]() – некоторый канонический вид квадратичной
формы. Предположим для простоты, что
– некоторый канонический вид квадратичной
формы. Предположим для простоты, что
![]() .
Выберем новые переменные
.
Выберем новые переменные
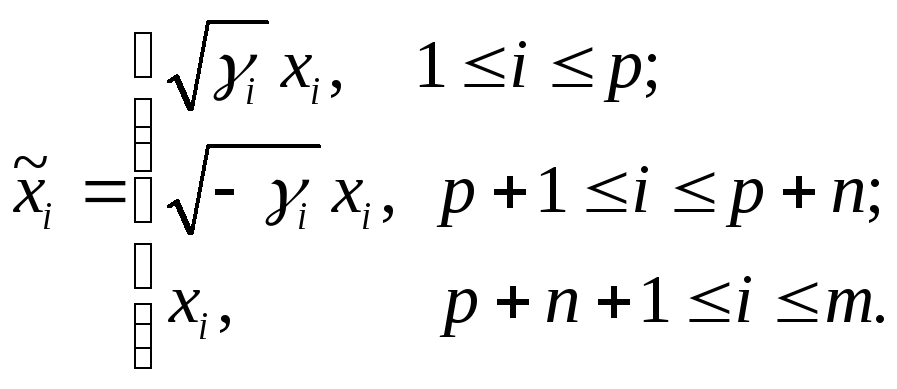
Тогда
![]()
![]() – другой канонический вид той же
квадратичной формы. Он получен из
предыдущего действительным линейным
невырожденным преобразованием независимых
переменных.
– другой канонический вид той же
квадратичной формы. Он получен из
предыдущего действительным линейным
невырожденным преобразованием независимых
переменных.
Определение.
Канонический вид квадратичной формы с
коэффициентами
![]() называют ее нормальным видом.
называют ее нормальным видом.
Что общего у
разных канонических видов, к которым
приводится одна и та же квадратичная
форма? По следствию из теоремы 4 для
любых двух ее канонических видов
![]()
![]()
![]()
![]()
![]() задающие их диагональные матрицы имеют
одинаковые ранги. Поэтому число ненулевых
членов во всех канонических видах
задающие их диагональные матрицы имеют
одинаковые ранги. Поэтому число ненулевых
членов во всех канонических видах
![]() одинаково; оно равно рангу матрицы
квадратичной формы и называется рангом
квадратичной формы. Но этим не
исчерпывается общность канонических
видов одной и той же
одинаково; оно равно рангу матрицы
квадратичной формы и называется рангом
квадратичной формы. Но этим не
исчерпывается общность канонических
видов одной и той же
![]() .
.
Теорема
9. (Закон инерции квадратичных
форм.) При любом преобразовании
квадратичной формы, определенной на
действительном линейном пространстве,
к её каноническому виду число
![]() положительных членов и число
положительных членов и число
![]() отрицательных членов в каноническом
виде будут одними и теми же.
отрицательных членов в каноническом
виде будут одними и теми же.
Доказательство.
Пусть
![]() ,
,
![]() – три базиса линейного пространства
– три базиса линейного пространства
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() и
и
![]() – матрицы перехода между базисами.
Пусть в базисе
– матрицы перехода между базисами.
Пусть в базисе
![]() (в переменных
(в переменных
![]() )
квадратичная форма имеет вид
)
квадратичная форма имеет вид
![]()
![]() .
Пусть в базисе
.
Пусть в базисе
![]() (в переменных
(в переменных
![]()
![]() )
она имеет канонический вид
)
она имеет канонический вид
![]()
![]() ,
где все коэффициенты
,
где все коэффициенты
![]() .
Пусть в базисе
.
Пусть в базисе
![]() (в переменных
(в переменных
![]()
![]() )
она имеет другой канонический вид
)
она имеет другой канонический вид
![]()
![]() ,
где все коэффициенты
,
где все коэффициенты
![]() .
.
Для любого
элемента
![]()
![]() имеем равенство
имеем равенство
![]()
![]() . (1)
. (1)
Предположим, что
![]() .
Тогда рассмотрим те элементы
.
Тогда рассмотрим те элементы
![]()
![]() ,
для которых
,
для которых
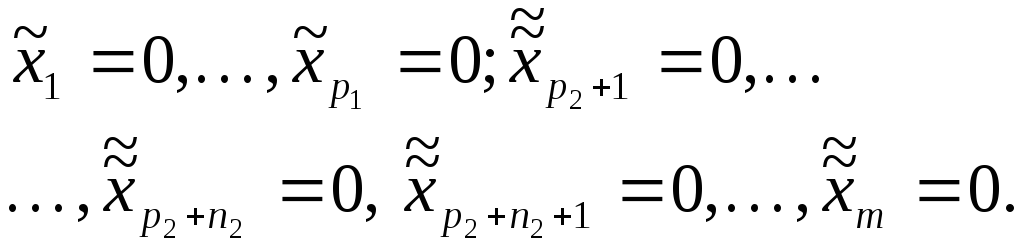 (2)
(2)
Поскольку
![]() ,
число условий в (2) меньше, чем
,
число условий в (2) меньше, чем
![]() .
При помощи линейных преобразований
.
При помощи линейных преобразований
![]() и
и
![]() выразим переменные
выразим переменные
![]() и переменные
и переменные
![]() через переменные
через переменные
![]() .
Тогда (2) является однородной системой
линейных алгебраических уравнений
относительно координат
.
Тогда (2) является однородной системой
линейных алгебраических уравнений
относительно координат
![]() элементов
элементов
![]() в базисе
в базисе
![]() .
В этой системе число уравнений меньше,
чем число
.
В этой системе число уравнений меньше,
чем число
![]() неизвестных. Поэтому по теореме 4 темы
3 система уравнений имеет ненулевое
решение
неизвестных. Поэтому по теореме 4 темы
3 система уравнений имеет ненулевое
решение
![]() .
То есть, в пространстве
.
То есть, в пространстве
![]() существует элемент
существует элемент
![]() ,
для которого выполнены условия (2).
,
для которого выполнены условия (2).
С другой стороны,
если некоторый элемент
![]()
![]() удовлетворяет условиям (2), то в равенстве
(1) левая часть равна нулю. Тогда из (1)
получаем
удовлетворяет условиям (2), то в равенстве
(1) левая часть равна нулю. Тогда из (1)
получаем
![]() .
Итак, если элемент
.
Итак, если элемент
![]()
![]() удовлетворяет (2), то в базисе
удовлетворяет (2), то в базисе
![]() все его координаты
все его координаты
![]() ,
т.е.
,
т.е.
![]() .
– Противоречие! Следовательно,
неравенство
.
– Противоречие! Следовательно,
неравенство
![]() невозможно.
невозможно.
Точно так же
доказывается, что невозможно неравенство
![]() .
Точно так же доказывается, что невозможны
неравенства
.
Точно так же доказывается, что невозможны
неравенства
![]() и
и
![]() .
.
Число
![]() положительных членов в каноническом
виде квадратичной формы называют ее
положительным индексом инерции.
Число
положительных членов в каноническом
виде квадратичной формы называют ее
положительным индексом инерции.
Число
![]() отрицательных членов в каноническом
виде квадратичной формы называют ее
отрицательным индексом инерции.
Пару чисел
отрицательных членов в каноническом
виде квадратичной формы называют ее
отрицательным индексом инерции.
Пару чисел
![]() называют сигнатурой квадратичной
формы. (Иногда сигнатурой называют число
называют сигнатурой квадратичной
формы. (Иногда сигнатурой называют число
![]() .)
Ясно, что сумма
.)
Ясно, что сумма
![]() равна рангу квадратичной формы. Если
равна рангу квадратичной формы. Если
![]()
![]() ,
то квадратичную форму называют
невырожденной; если
,
то квадратичную форму называют
невырожденной; если
![]()
![]() , то – вырожденной.
, то – вырожденной.
Квадратичную
форму
![]() называют неотрицательной, если
называют неотрицательной, если
![]()
![]() для всех
для всех![]()
![]() . Квадратичную форму называют строго
положительной (или положительно
определенной), если для любого
. Квадратичную форму называют строго
положительной (или положительно
определенной), если для любого
![]()
![]() из условия
из условия
![]() следует
следует
![]()
![]() .
.
Теорема
10. Квадратичная форма является
положительно определенной в том и только
в том случае, если ее положительный
индекс инерции
![]() .
.
Доказательство.
Пусть
![]() ,
и в некотором базисе
,
и в некотором базисе
![]() квадратичная форма
квадратичная форма
![]() приведена к нормальному виду:
приведена к нормальному виду:
![]()
![]()
![]() .
.
Если
![]() является положительно определенной,
то в ее нормальном виде нет отрицательных
или равных нулю членов. В противном
случае для некоторого элемента
является положительно определенной,
то в ее нормальном виде нет отрицательных
или равных нулю членов. В противном
случае для некоторого элемента
![]()
![]() ,
координаты которого в базисе
,
координаты которого в базисе
![]() равны, например,
равны, например,
![]() ,
выполнено неравенство
,
выполнено неравенство
![]() ;
а для некоторого
;
а для некоторого
![]()
![]() ,
координаты которого в базисе
,
координаты которого в базисе
![]() равны, например,
равны, например,
![]() ,
выполнено равенство
,
выполнено равенство
![]() ,
хотя
,
хотя
![]() .
Поэтому
.
Поэтому
![]() .
.
Если же в
нормальном виде квадратичной формы
![]() ,
т.е.
,
т.е.
![]()
![]() ,
то
,
то
![]() для любого
для любого
![]()
![]() ,
причем
,
причем
![]() только при
только при
![]() .
.
Важность класса
положительно определенных квадратичных
форм объясняется следующим обстоятельством.
Пусть
![]() – положительно определенная квадратичная
форма, а
– положительно определенная квадратичная
форма, а
![]() – ее полярная билинейная форма. Тогда
– ее полярная билинейная форма. Тогда
![]() обладает свойствами:
обладает свойствами:
-
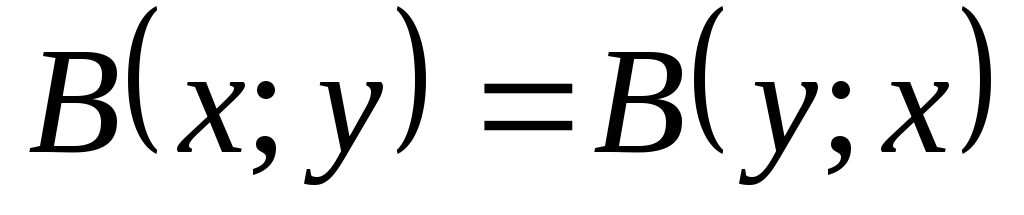 для любых
для любых
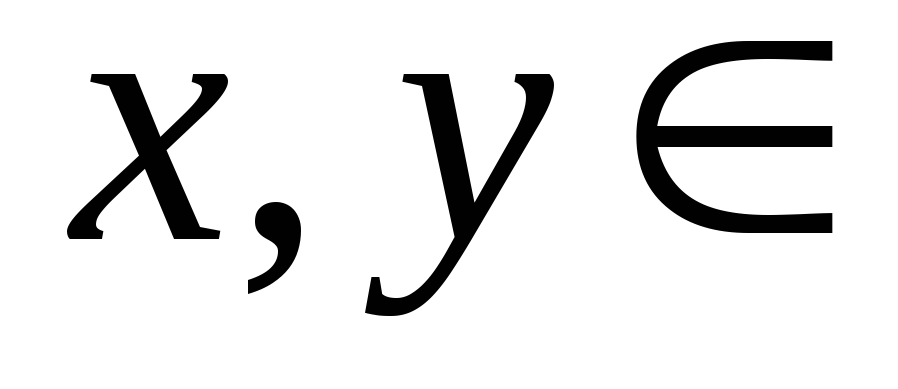
 .
. -
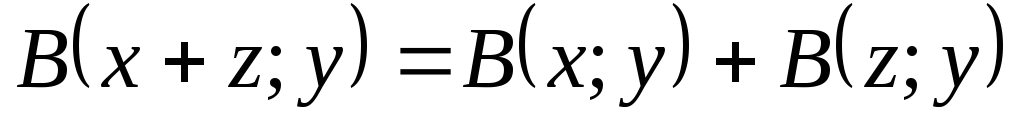 для любых
для любых
 .
. -
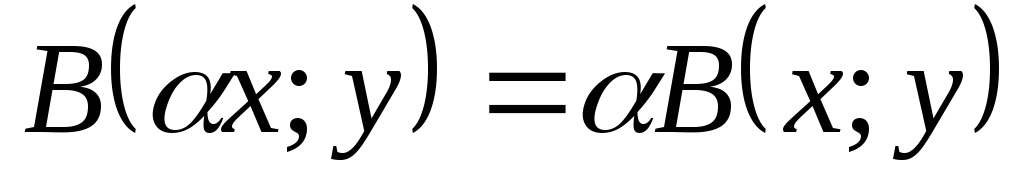 для любых
для любых
 ,
,
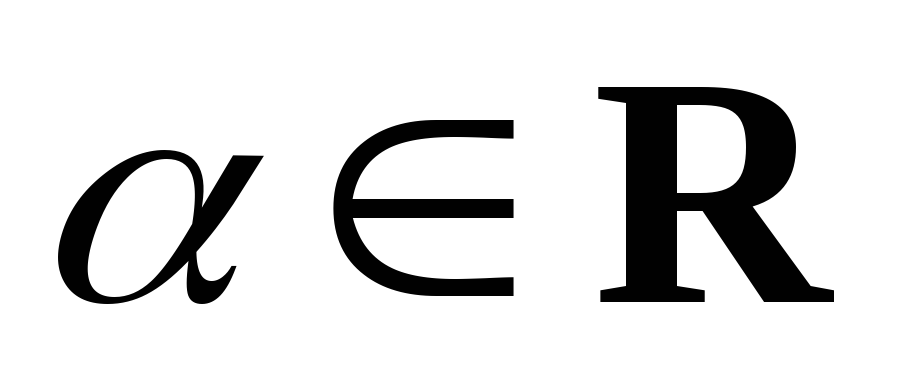 .
. -
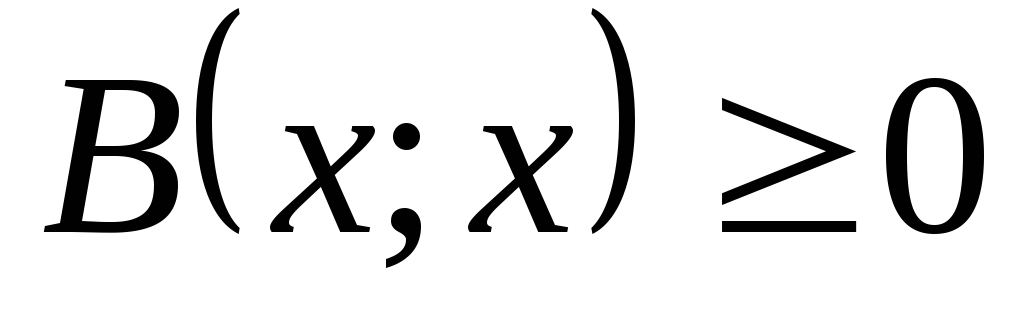 , причем
, причем
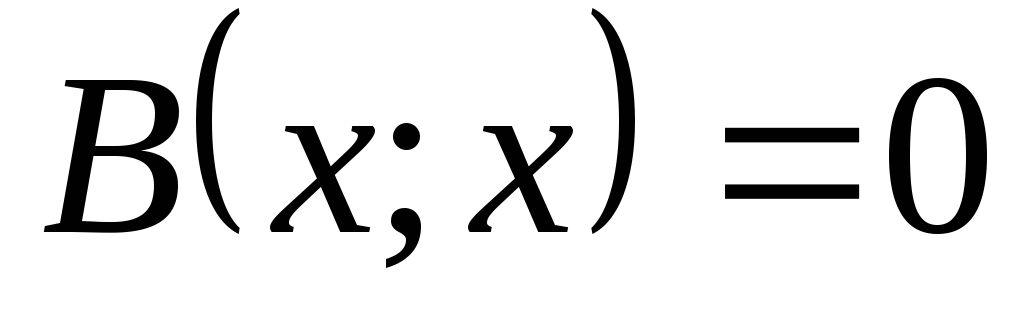 только для
только для
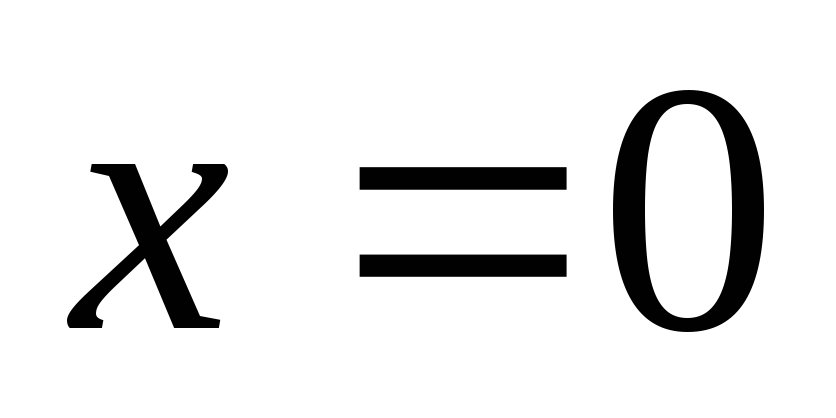

 .
.
Тем самым
![]() удовлетворяет всем аксиомам скалярного
произведения в действительном линейном
пространстве. Справедливо
удовлетворяет всем аксиомам скалярного
произведения в действительном линейном
пространстве. Справедливо
Утверждение. Скалярное произведение в действительном линейном пространстве является билинейной формой, полярной к положительно определенной квадратичной форме. Любая такая билинейная форма может быть принята за скалярное произведение.
Квадратичную
форму
![]() естественно назвать неположительной,
если
естественно назвать неположительной,
если
![]() для всех
для всех
![]()
![]() ,
и строго отрицательной (или
отрицательно определенной), если из
условия
,
и строго отрицательной (или
отрицательно определенной), если из
условия
![]() следует
следует
![]() .
Очевидно, что
.
Очевидно, что
![]() является отрицательно определенной в
том и только в том случае, если ее
отрицательный индекс инерции
является отрицательно определенной в
том и только в том случае, если ее
отрицательный индекс инерции
![]() .
.
Квадратичную
форму называют знакопеременной,
если для некоторого
![]()
![]()
![]() ,
а для некоторого
,
а для некоторого
![]()
![]()
![]() .
.
Задача.
В терминах индексов инерции найдите
необходимые и достаточные условия того,
что
![]() неотрицательна;
неотрицательна;
![]() неположительна;
неположительна;
![]() знакопеременна.
знакопеременна.
