2. Билинейные формы.

Будем рассматривать и как независимые переменные, пробегающие все линейное пространство над полем . Введем отображение , причем будем считать, что значения определяются только элементами и не зависят от выбора базиса в . называют билинейной формой, если при каждом фиксированном является линейной формой от , а при каждом фиксированном – линейной формой от .

Примеры билинейных форм.

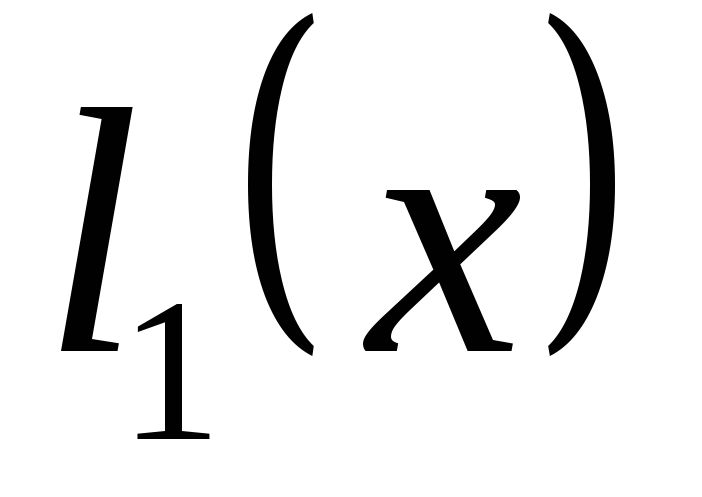
1. Если и – линейные формы, определенные на пространстве , , то  является билинейной формой.

2. . Пусть фиксирована непрерывная функция двух переменных . Для каждой пары непрерывных функций положим . В частности, если , то – произведение линейных функционалов.

3. , , . Пусть фиксирована матрица . Положим .

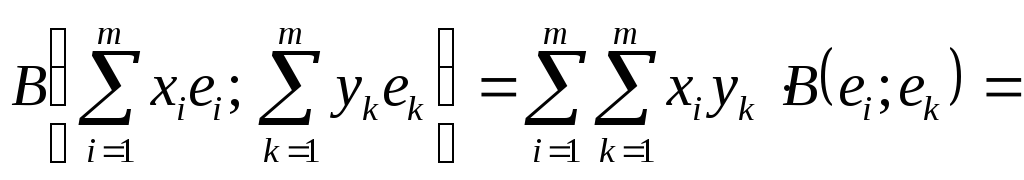
Если и – базис пространства , то , и билинейная форма в базисе имеет вид . Коэффициенты составляют матрицу билинейной формы в базисе .

Пусть и – два базиса в , связанные матрицей перехода . Тогда из разложений , получаем выражения билинейной формы в базисах и : .

Введем обозначения -матриц билинейной формы в базисах и : , . Как связаны матрицы и ?

Теорема 4. Если , то .

(Докажите самостоятельно.)

Следствие. .

Поскольку ранг матрицы билинейной формы не зависит от выбора базиса в пространстве , это число естественно назвать рангом билинейной формы. Отметим еще, что .

Билинейные формы, определенные на , можно складывать и умножать на числа из поля ; при этом будут получаться новые билинейные формы.

Теорема 5. Множество всех билинейных форм, определенных на линейном пространстве , является линейным пространством. Если , то размерность пространства всех билинейных форм на равна .

(Докажите самостоятельно.)

Задача. Найдите базис в пространстве билинейных форм ().

Рассмотрим два важных класса билинейных форм. Билинейную форму называют симметричной, если для любых . Билинейную форму называют кососимметричной, если для любых .

Пример. В действительном евклидовом пространстве скалярное произведение является симметричной билинейной формой. 

В базисе коэффициенты билинейной формы , поэтому матрица симметричной билинейной формы симметрична: для всех и , а матрица кососимметричной билинейной формы кососимметрична: для всех и (в частности, все ).

Теорема 6. В линейном пространстве всех билинейных форм, определенных на , множество всех симметричных билинейных форм образует подпространство; множество всех кососимметричных билинейных форм также образует подпространство. Пространство всех билинейных форм является прямой суммой этих двух подпространств.

Доказательство. Очевидно, что если и – симметричные билинейные формы, то и – симметричная билинейная форма, каковы бы ни были . Это значит, что симметричные билинейные формы образуют подпространство.

Если и – кососимметричные билинейные формы, то и – кососимметричная билинейная форма при любых . Это значит, что кососимметричные билинейные формы образуют подпространство.

Ясно, что билинейная форма может быть одновременно симметричной и кососимметричной в том и только в том случае, если она нулевая, т.е. для любых . Следовательно, сумма двух рассматриваемых подпространств является прямой суммой. С другой стороны, всякую билинейную форму можно представить в виде суммы симметричной и кососимметричной билинейных форм: ; – симметричная, – кососимметричная. Поэтому прямая сумма двух рассматриваемых подпространств совпадает со всем пространством билинейных форм. 

Замечание. Если , то размерность подпространства всех симметричных билинейных форм равна , а размерность подпространства всех кососимметричных билинейных форм равна .

(Докажите самостоятельно, рассмотрев матрицы симметричных и кососимметричных билинейных форм в некотором фиксированном базисе пространства .) 