
- •Тема 8. Линейные операторы в евклидовых и в унитарных пространствах.
- •1. Сопряженные операторы.
- •2. Самосопряженные операторы.
- •3. Нормальные операторы.
- •4. Унитарные операторы.
- •5. Ортогональные операторы.
- •Тема 9. Линейные, билинейные и квадратичные формы.
- •1. Линейные формы.
- •2. Билинейные формы.
- •3. Квадратичные формы.
- •4. Методы приведения квадратичной формы к каноническому виду.
5. Ортогональные операторы.
Пусть теперь
![]() является действительным евклидовым
пространством. Аналогом унитарного
оператора в этом случае служит
ортогональный оператор.
является действительным евклидовым
пространством. Аналогом унитарного
оператора в этом случае служит
ортогональный оператор.
Определение.
Линейный оператор
![]() , действующий в евклидовом пространстве,
называют ортогональным, если
, действующий в евклидовом пространстве,
называют ортогональным, если
![]() .
.
Легко проверить, что теорема 14 и оба следствия из нее остаются в силе, если в них унитарный оператор в унитарном пространстве заменить на ортогональный оператор в евклидовом пространстве. Нужно только в доказательстве следствия 1 вместо тождества (11) использовать тождество
![]() ,
,
справедливое в евклидовом пространстве. Точно так же сохраняется и теорема 16.
Различия между унитарным и ортогональным операторами не только терминологические, они проявляются в канонической форме их матриц (вспомните теоремы 8* и 9 темы 7).
Запишем условия
ортогональности оператора
![]() в матричной форме. Для этого выберем
произвольный ортонормированный
базис
в матричной форме. Для этого выберем
произвольный ортонормированный
базис
![]() .
Пусть в этом базисе оператор
.
Пусть в этом базисе оператор
![]() имеет матрицу
имеет матрицу
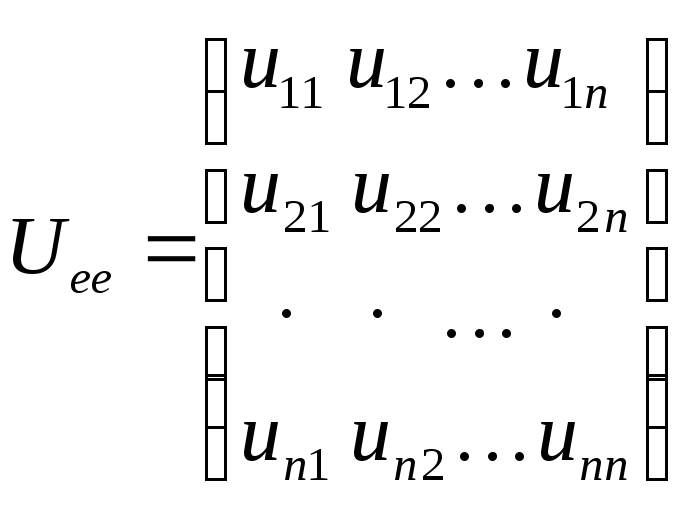 ,
все
,
все
![]() .
.
В том же базисе
![]() оператор
оператор
![]() имеет матрицу, транспонированную к
имеет матрицу, транспонированную к
![]() :
:
![]() .
Требование ортогональности означает,
что
.
Требование ортогональности означает,
что
![]() – единичная
– единичная
![]() -матрица.
Перемножим эти матрицы:
-матрица.
Перемножим эти матрицы:
![]()
 (14)
(14)
Условие ортогональности можно
записать и в виде
![]() .
Тогда имеем
.
Тогда имеем
![]()
 (15)
(15)
Действительную
![]() -матрицу,
элементы которой удовлетворяют (14) или
(15), называют ортогональной.
-матрицу,
элементы которой удовлетворяют (14) или
(15), называют ортогональной.
Для ортогональной
матрицы
![]() из условия
из условия
![]() вытекает
вытекает
![]() ,
т.е.
,
т.е.
![]() или
или
![]() .
.
Дадим геометрическое описание действия ортогонального оператора и построим каноническую форму его матрицы. Сначала рассмотрим действие ортогонального оператора в одномерном и в двумерном евклидовых пространствах.
Пример.
Одномерное действительное пространство
![]() изоморфно
изоморфно
![]() .
Матрица ортогонального оператора в
этом случае может иметь вид
.
Матрица ортогонального оператора в
этом случае может иметь вид
![]() ,
либо
,
либо
![]() .
Геометрическое действие такого оператора
не требует пояснений.
.
Геометрическое действие такого оператора
не требует пояснений.
Пример.
Двумерное действительное пространство
![]() изоморфно
изоморфно
![]() .
Матрица ортогонального оператора в
ортонормированном базисе
.
Матрица ортогонального оператора в
ортонормированном базисе
![]() в
в
![]() имеет вид
имеет вид
![]()
![]() ,
причем
,
причем
![]()
![]() .
Вспомним явное выражение обратной
матрицы:
.
Вспомним явное выражение обратной
матрицы:
![]() ,
где
,
где
![]()
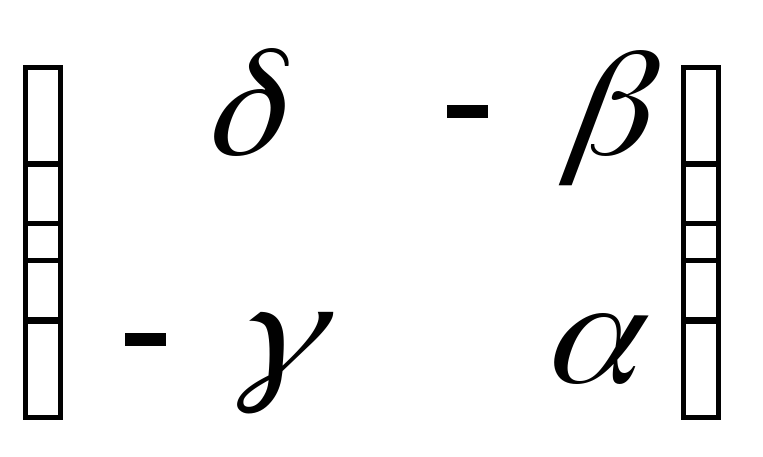 – матрица, присоединенная к
– матрица, присоединенная к
![]() .
.
Пусть
![]() .
Тогда
.
Тогда
![]()
![]()
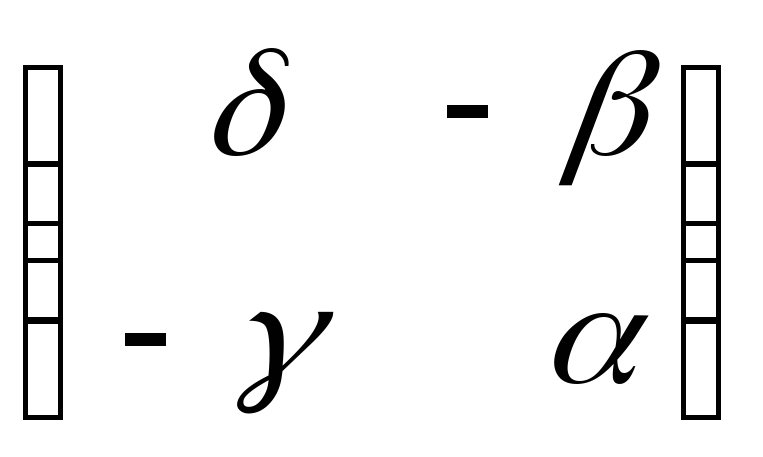 .
Отсюда
.
Отсюда
![]()
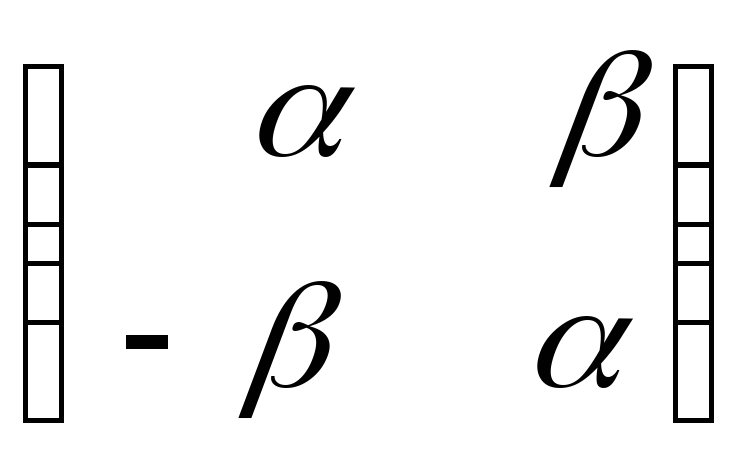 ,
причем
,
причем
![]() .
Это позволяет положить
.
Это позволяет положить
![]() ,
,
![]() ,
т.е.
,
т.е.
![]()
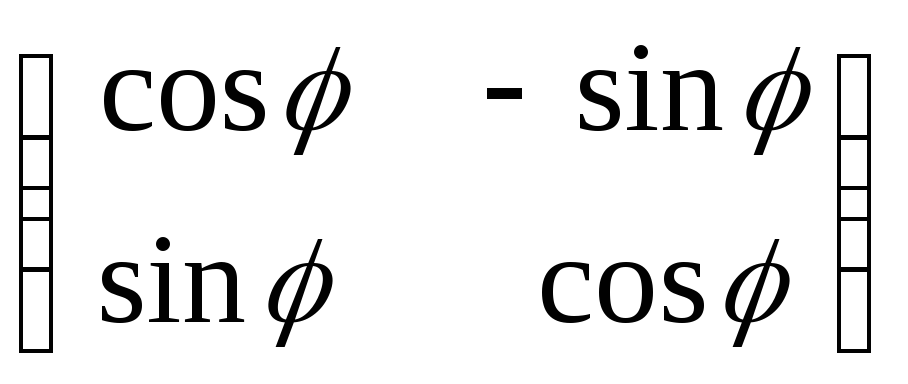 .
Найдем характеристический многочлен
рассматриваемого оператора:
.
Найдем характеристический многочлен
рассматриваемого оператора:
![]() .
Если
.
Если
![]() ,
то имеем собственные значения
,
то имеем собственные значения
![]() .
Тогда ортонормированный базис
.
Тогда ортонормированный базис
![]() состоит из собственных векторов, и
состоит из собственных векторов, и
![]()
![]()
![]() :
тождественный оператор
:
тождественный оператор
![]() оставляет на своем месте любой вектор.
Если
оставляет на своем месте любой вектор.
Если
![]() ,
то имеем собственные значения
,
то имеем собственные значения
![]() .
Тогда ортонормированный базис
.
Тогда ортонормированный базис
![]() состоит из собственных векторов, и
состоит из собственных векторов, и
![]()
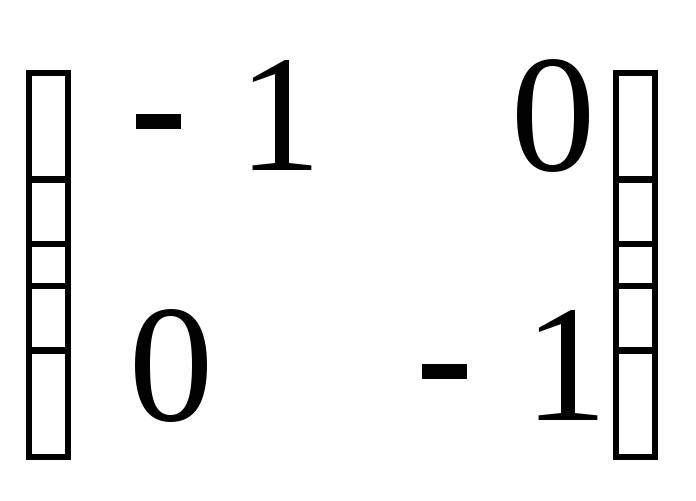
![]() :
оператор
:
оператор
![]() отражает любой вектор относительно
обеих осей координат. Если
отражает любой вектор относительно
обеих осей координат. Если
![]() ,
то собственных значений нет; имеется
двумерное инвариантное подпространство
оператора
,
то собственных значений нет; имеется
двумерное инвариантное подпространство
оператора
![]() – все пространство
– все пространство
![]() .
Оператор
.
Оператор
![]() поворачивает любой вектор на угол
поворачивает любой вектор на угол
![]() против часовой стрелки вокруг начала
координат.
против часовой стрелки вокруг начала
координат.
Пусть теперь
![]() .
Тогда
.
Тогда
![]()
![]()
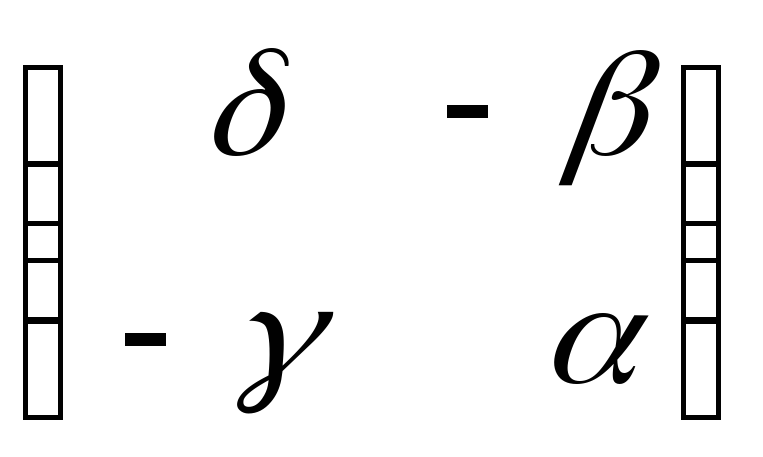 .
Отсюда
.
Отсюда
![]()
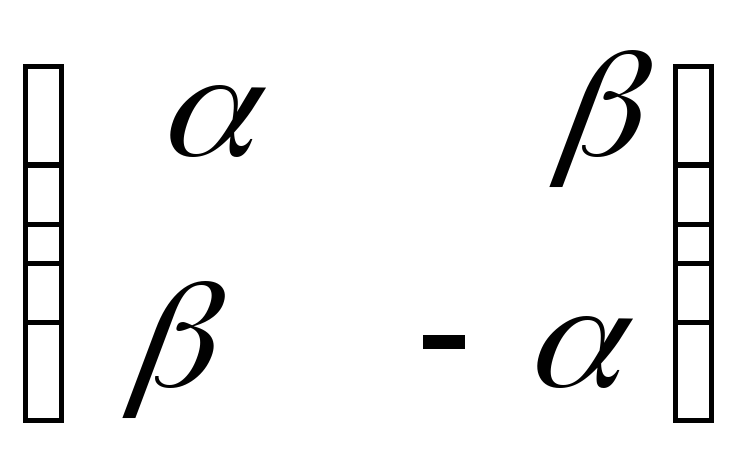 ,
причем
,
причем
![]() .
В этом случае характеристический
многочлен
.
В этом случае характеристический
многочлен
![]()
![]() .
Если собственные значения
.
Если собственные значения
![]() ,
,
![]() ,
то базисные векторы
,
то базисные векторы
![]() являются собственными, и
являются собственными, и
![]()
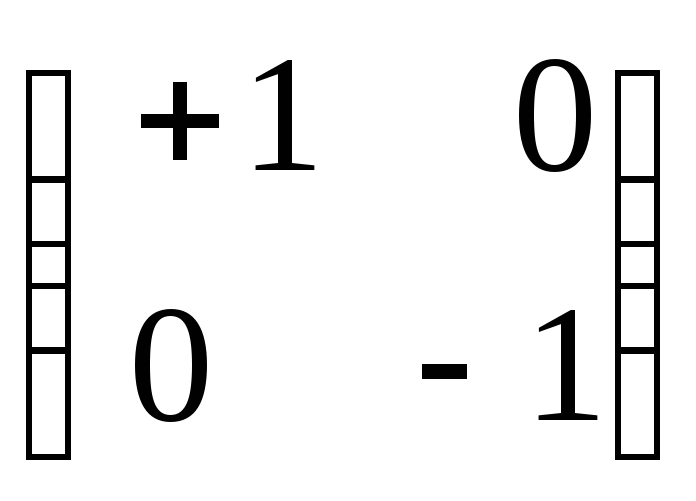 :
оператор
:
оператор
![]() отражает любой вектор относительно оси
отражает любой вектор относительно оси
![]() .
Если
.
Если
![]() ,
,
![]() ,
то базисные векторы
,
то базисные векторы
![]() являются собственными, и
являются собственными, и
![]()
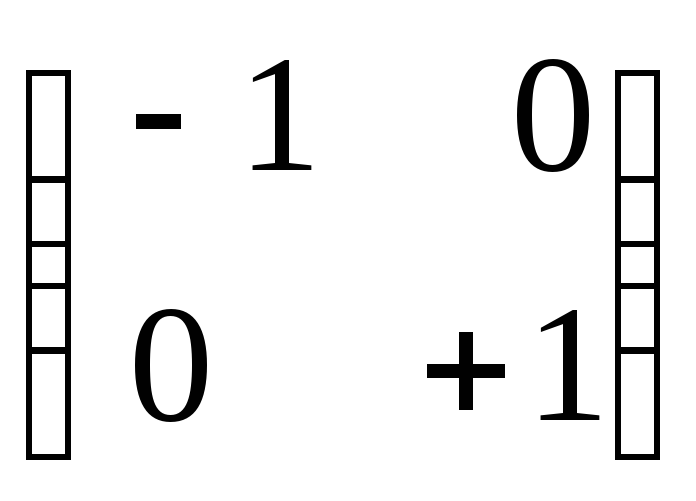 :
оператор
:
оператор
![]() отражает любой вектор относительно оси
отражает любой вектор относительно оси
![]() .
.
Теорема
19. (Каноническая форма матрицы
ортогонального оператора.) Для любого
ортогонального оператора
![]() ,
действующего в евклидовом пространстве
,
действующего в евклидовом пространстве
![]() ,
существует ортонормированный базис
,
существует ортонормированный базис
![]() ,
в котором его матрица
,
в котором его матрица
![]() имеет квазидиагональную форму. На
главной диагонали этой матрицы стоят
клетки вида
имеет квазидиагональную форму. На
главной диагонали этой матрицы стоят
клетки вида
![]() (им отвечают одномерные собственные
подпространства), или
(им отвечают одномерные собственные
подпространства), или
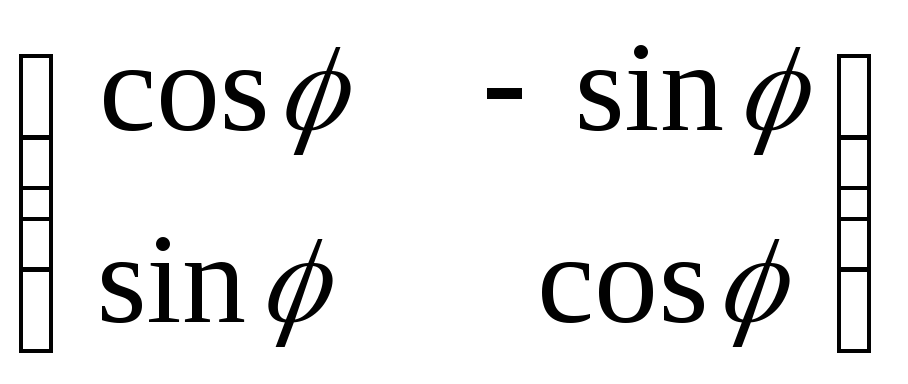 (им отвечают двумерные инвариантные
подпространства), или
(им отвечают двумерные инвариантные
подпространства), или
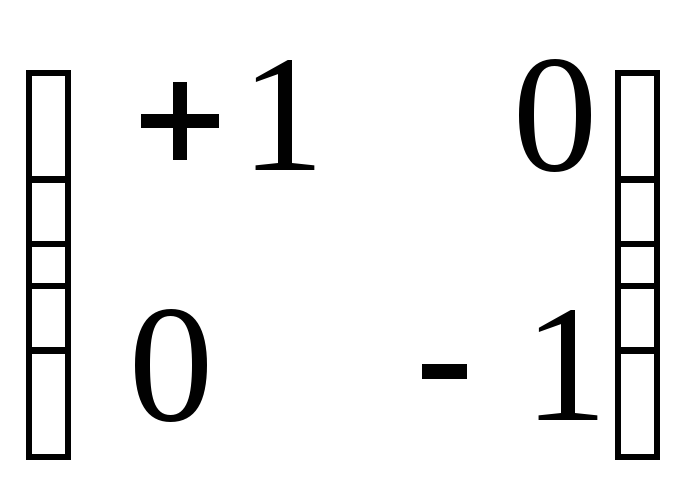 ,
,
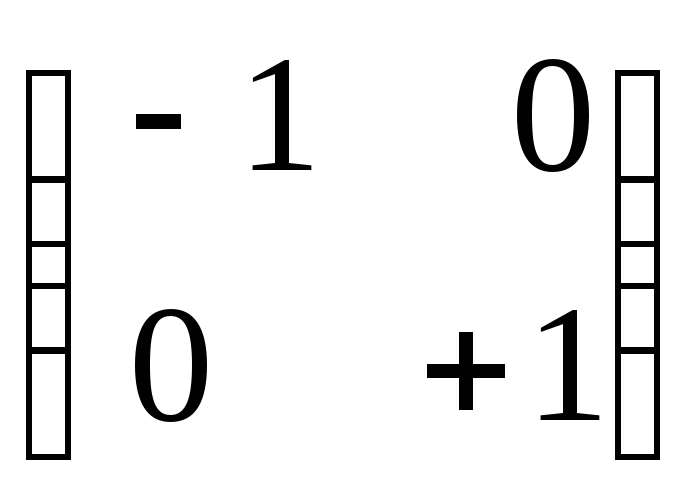 (им отвечают пары одномерных собственных
подпространств).
(им отвечают пары одномерных собственных
подпространств).
Доказательство
проведем индукцией по размерности
![]() пространства
пространства
![]() .
При
.
При
![]() теорема была доказана в предыдущих
примерах. Пусть
теорема была доказана в предыдущих
примерах. Пусть
![]() и теорема верна для ортогональных
операторов во всех пространствах
размерности не более
и теорема верна для ортогональных
операторов во всех пространствах
размерности не более
![]() .
Докажем теорему для пространств
размерности
.
Докажем теорему для пространств
размерности
![]() .
По теореме 9 темы 7 у всякого линейного
оператора
.
По теореме 9 темы 7 у всякого линейного
оператора
![]() в действительном пространстве имеется
одномерное или двумерное инвариантное
подпространство
в действительном пространстве имеется
одномерное или двумерное инвариантное
подпространство
![]() .
По теореме 16, справедливой для ортогональных
операторов, индуцированный оператор
.
По теореме 16, справедливой для ортогональных
операторов, индуцированный оператор
![]() является ортогональным. Если
является ортогональным. Если
![]()
![]() ,
то для ортогонального оператора
,
то для ортогонального оператора
![]() существует базис
существует базис
![]() ,
в котором его матрица имеет вид
,
в котором его матрица имеет вид
![]() или
или
![]() .
Если
.
Если
![]()
![]() ,
то для ортогонального оператора
,
то для ортогонального оператора
![]() существует ортонормированный базис
существует ортонормированный базис
![]() ,
в котором его матрица имеет вид
,
в котором его матрица имеет вид
![]()
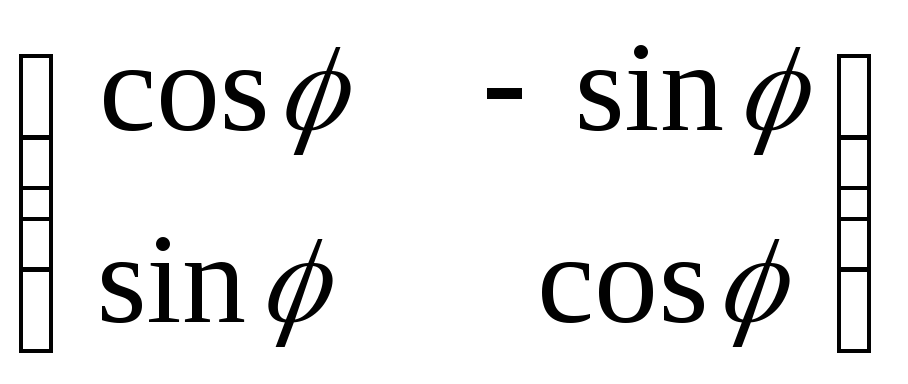 ,
или
,
или
![]()
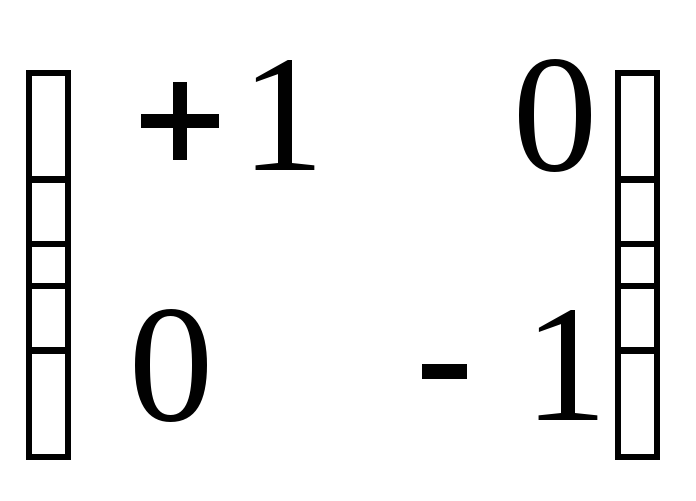 ,
или
,
или
![]()
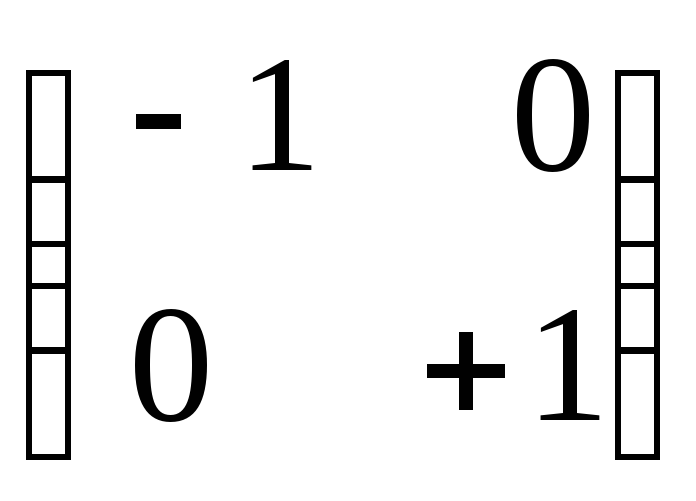 .
.
По теореме 16
![]() инвариантно относительно оператора
инвариантно относительно оператора
![]() .
Поскольку
.
Поскольку
![]()
![]() ,
по предположению индукции в
,
по предположению индукции в
![]() существует ортонормированный базис, в
котором матрица оператора
существует ортонормированный базис, в
котором матрица оператора
![]() имеет требуемый вид. Тогда в базисе
всего пространства
имеет требуемый вид. Тогда в базисе
всего пространства
![]() матрица оператора
матрица оператора
![]() будет иметь требуемый вид.
будет иметь требуемый вид.
Ортогональная матрица является матрицей ортогонального оператора в ортонормированном базисе. А переход от одного ортонормированного базиса к другому ортонормированному базису в евклидовом пространстве задается ортогональным оператором. Поэтому основным результатом для ортогональных матриц является
Теорема
20. Пусть
![]() – ортогональная матрица. Тогда существует
такая ортогональная матрица
– ортогональная матрица. Тогда существует
такая ортогональная матрица
![]() ,
что
,
что
![]() ,
где
,
где
![]() – квазидиагональная ортогональная
матрица, описанная в теореме 19.
– квазидиагональная ортогональная
матрица, описанная в теореме 19.
Теорема 20
утверждает, что ортогональная матрица
![]() ортогонально подобна квазидиагональной
матрице
ортогонально подобна квазидиагональной
матрице
![]() .
Если у ортогонального оператора имеются
собственные значения, то они равны +1
или
.
Если у ортогонального оператора имеются
собственные значения, то они равны +1
или
![]() и стоят на диагонали матрицы
и стоят на диагонали матрицы
![]() .
.
Напомним, что
если самосопряженный оператор действует
в действительном пространстве, то
в ортонормированном базисе его матрица
симметрична:
![]() .
Рассуждениями, аналогичными доказывающим
теорему 20, получаем основной результат
для симметричных действительных матриц:
.
Рассуждениями, аналогичными доказывающим
теорему 20, получаем основной результат
для симметричных действительных матриц:
Теорема
21. Пусть
![]() – симметричная действительная матрица.
Тогда существует такая ортогональная
матрица
– симметричная действительная матрица.
Тогда существует такая ортогональная
матрица
![]() ,
что
,
что
![]() ,
где
,
где
![]() – действительная диагональная матрица.
– действительная диагональная матрица.
(Докажите самостоятельно.)
Теорема 21
утверждает, что действительная
симметричная матрица
![]() ортогонально подобна матрице
ортогонально подобна матрице
![]() .
.
