3. Нормальные операторы.

Продолжим намеченную ранее аналогию между комплексными числами и линейными операторами в унитарном пространстве. Всякое комплексное число удовлетворяет условию . Возникает вопрос: для всех ли линейных операторов выполнено равенство ? Следующий пример дает отрицательный ответ на этот вопрос.

Пример. Пусть – ортонормированный базис в , и 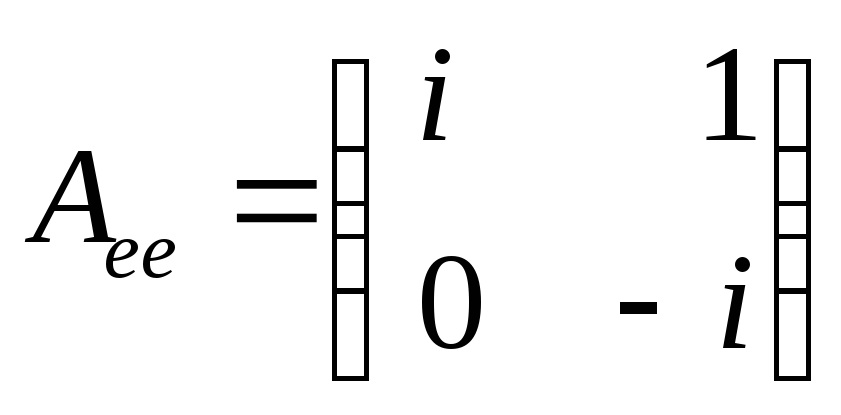( – мнимая единица). Тогда ,

.

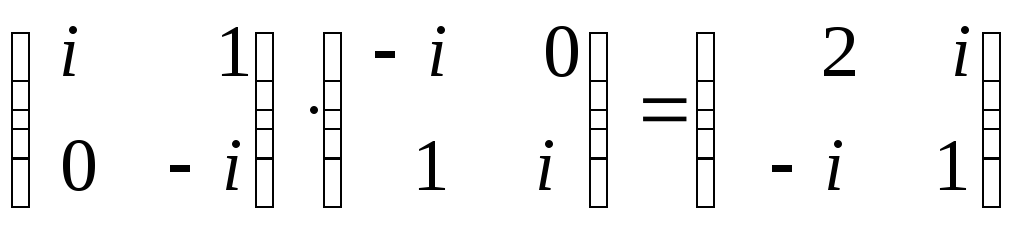Поэтому .

Определение. Оператор называют нормальным, если .

Пусть , и в некотором ортонормированном базисе матрица этого оператора диагональна:

.

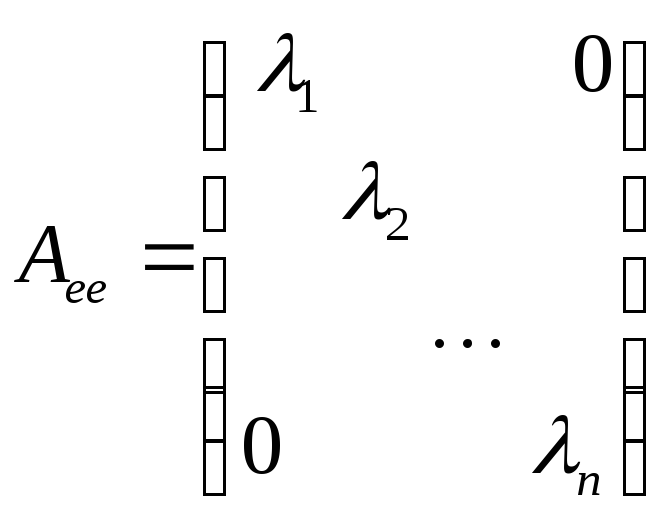В этом же базисе матрица оператора имеет вид

.

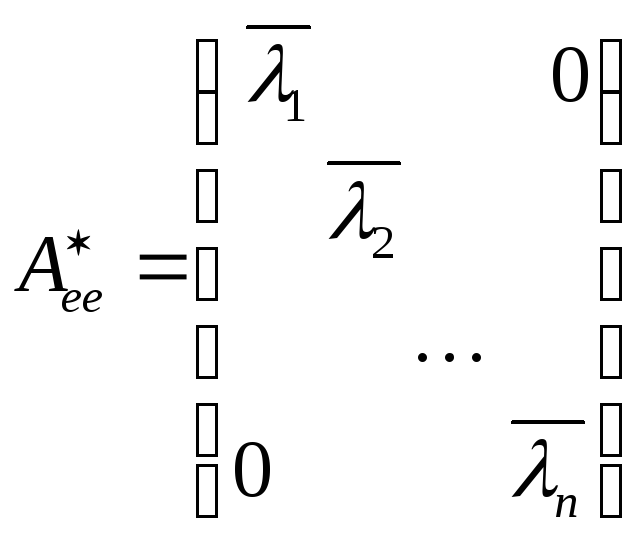Диагональные матрицы перестановочны, поэтому перестановочны и сами операторы и , т.е. рассматриваемый оператор нормален. Оказывается, что этим случаем полностью исчерпывается класс нормальных операторов: справедлива

Теорема 13. Оператор является нормальным в том и только в том случае, если в пространстве существует ортонормированный базис, в котором матрица этого оператора диагональна.

(Без доказательства. Доказательство см в [1, 3, 4, 5].)

Нормальный оператор обладает следующими свойствами (докажите их самостоятельно).

Свойство 1. Пусть – нормальный оператор. Если , , то для того же вектора выполнено равенство .

Свойство 2. Пусть – нормальный оператор. Тогда . 

Свойство 3. Пусть – нормальный оператор. Тогда , . 

Свойство 4. Пусть – нормальный оператор. Если , , и , ,где , то .

Свойство 5. Пусть – нормальный оператор. Тогда операторы и имеют общий ортонормированный базис, целиком состоящий из их собственных векторов. 

Свойство 6. Нормальный оператор является самосопряженным в том и только в том случае, если все его собственные значения действительны. 

4. Унитарные операторы.

Аналогом множества комплексных чисел , удовлетворяющих условию , является еще один важный класс операторов, действующих в унитарном пространстве.

Определение. Линейный оператор , действующий в унитарном пространстве, называют унитарным, если .

Замечание. В конечномерном пространстве условия и эквивалентны. В бесконечномерном пространстве эти два условия были бы различными. 

Из определения ясно, что унитарный оператор нормален. Основное свойство унитарного оператора состоит в том, что . Понятие унитарного оператора имеет простой геометрический смысл:

Теорема 14. Линейный оператор , действующий в унитарном пространстве , является унитарным в том и только в том случае, если он сохраняет скалярное произведение: для любых .

Доказательство. Пусть – унитарный оператор. Тогда для любых имеем .

Обратно: пусть для любых . Тогда . В силу произвольности из последнего равенства получаем для любого . Это значит, что . Докажем, что оператор невырожденный. Предположим противное: для некоторого . Тогда , т.е. скалярное произведение не сохраняется. Итак, оператор невырожденный, поэтому существует обратный к нему оператор . Из равенства получаем , т.е. – унитарный оператор.

Следствие 1. Линейный оператор , действующий в унитарном пространстве , является унитарным в том и только в том случае, если он сохраняет евклидову норму каждого вектора: для любого .

Доказательство. Пусть – унитарный оператор. Тогда для любого имеем , т.е. .

Обратно: пусть оператор сохраняет евклидову норму каждого вектора, т.е. для любого . Заметим, что в унитарном пространстве выполнено тождество

(11)

(проверьте самостоятельно; здесь – мнимая единица).

Из (11) в силу линейности оператора и сохранения им евклидовой нормы получаем

.

Следствие 2. Если – унитарный оператор, то любую ортонормированную систему векторов он переводит снова в ортонормированную систему. Если линейный оператор переводит какой-либо ортонормированный базис снова в ортонормированный базис , то – унитарный оператор.

Доказательство. Первое утверждение непосредственно следует из теоремы 14. Докажем второе утверждение. Пусть в ортонормированном базисе элементы имеют разложения по базису , . Тогда . В силу линейности оператора имеем , . Поскольку по условию – тоже ортонормированный базис, то снова имеем . Следовательно, для любых .

Теорема 15. Нормальный оператор является унитарным в том и только в том случае, если все его собственные значения по модулю равны единице.

Доказательство. Пусть – унитарный оператор, и , . Можно считать, что . В самом деле, в противном случае пронормируем этот собственный вектор: является собственным вектором, отвечающим тому же собственному числу . Тогда имеем

.

Обратно: пусть – нормальный оператор, все собственные числа которого по модулю равны единице. По теореме 13 оператор имеет ортонормированный базис , состоящий из его собственных векторов. В этом базисе матрица оператора имеет вид

,

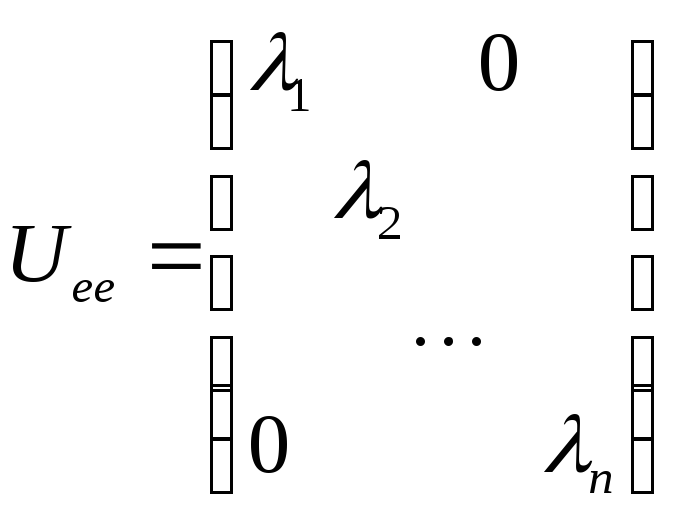где – собственные числа оператора ; по условию теоремы , . Для сопряженного оператора все векторы базиса также являются собственными векторами, но отвечают собственным числам . В базисе матрица оператора имеет вид

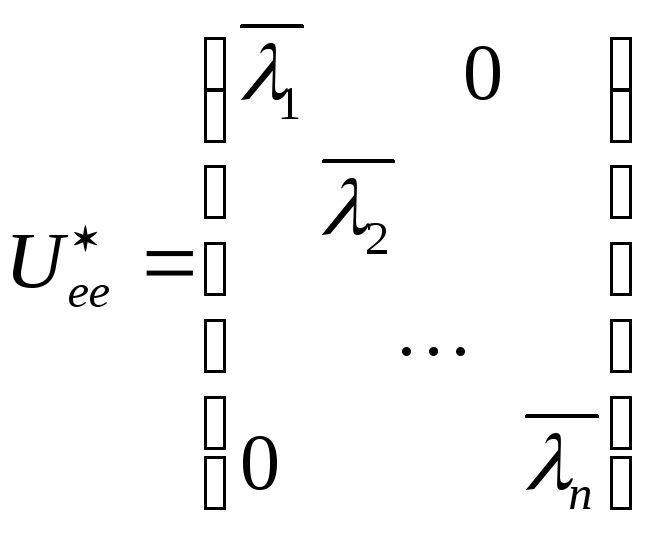
(см. свойство 5 нормального оператора). Пусть . Тогда . В силу произвольности это означает, что . Аналогично доказывается, что .

Теорема 16. Пусть – инвариантное подпространство унитарного оператора . Тогда индуцированный оператор является унитарным оператором, действующим в . Кроме того, является подпространством в , также инвариантным относительно .

Доказательство. Оператор является унитарным в , так как он сохраняет скалярные произведения.

является невырожденным в пространстве оператором, так как он унитарный. Поэтому .Следовательно, для любого элемента существует такой элемент , что . Тогда для любого имеем (поскольку ). Этим доказано, что если , то и .

Запишем условия унитарности оператора в матричной форме. Для этого выберем произвольный ортонормированный базис . Пусть в этом базисе оператор имеет матрицу

.

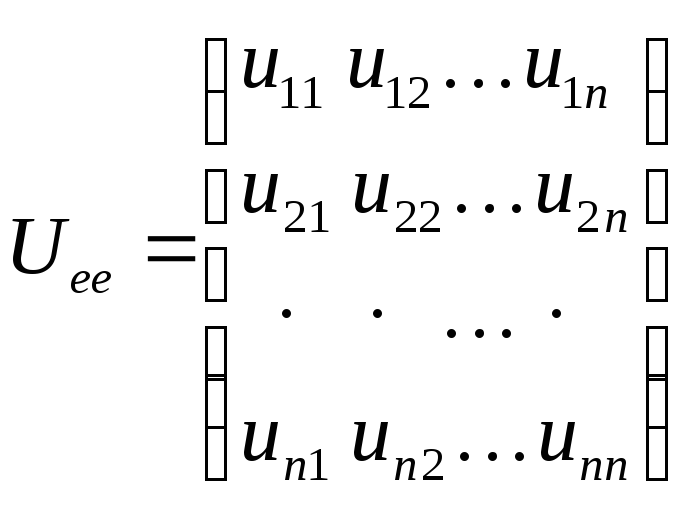В том же базисе оператор имеет матрицу, сопряженную к :

.

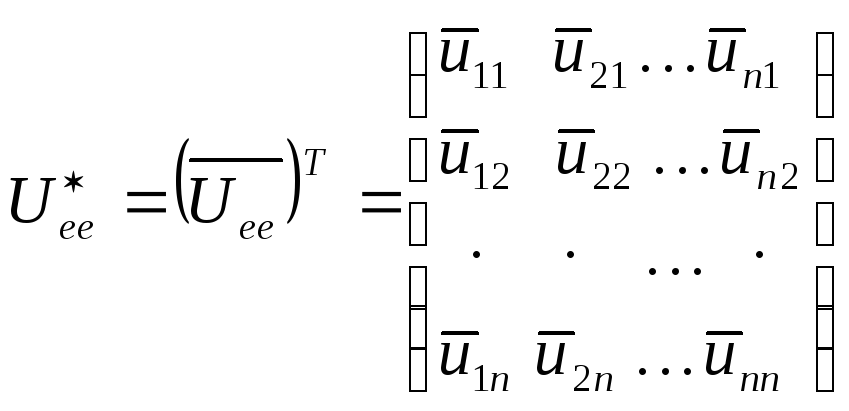Требование унитарности означает, что – единичная -матрица. Перемножим эти матрицы:

(12)

Условие унитарности можно записать и в виде . Тогда имеем

(13)

Матрицу, элементы которой удовлетворяют (12) или (13), называют унитарной.

Унитарная матрица является матрицей унитарного оператора в ортонормированном базисе. А по следствию 2 переход от одного ортонормированного базиса к другому ортонормированному базису задается унитарным оператором. Поэтому основным результатом для унитарных матриц является

Теорема 17. Пусть – унитарная матрица. Тогда существует такая унитарная матрица , что , где – диагональная матрица, у которой на диагонали стоят числа, по модулю равные единице.

Теорема 17 утверждает, что унитарная матрица унитарно подобна матрице .

Аналогичными рассуждениями получаем основной результат для самосопряженных матриц:

Теорема 18. Пусть – самосопряженная матрица. Тогда существует такая унитарная матрица , что , где – диагональная матрица, у которой на диагонали стоят действительные числа.

(Докажите самостоятельно.)

Теорема 18 утверждает, что самосопряженная матрица унитарно подобна матрице .