Тема 9. Линейные, билинейные и квадратичные формы.

1. Линейные формы.

Пусть – линейное пространство над полем ( или ). Линейное отображение : называют линейной формой (или линейным функционалом); , для всех , .

Примеры линейных форм.

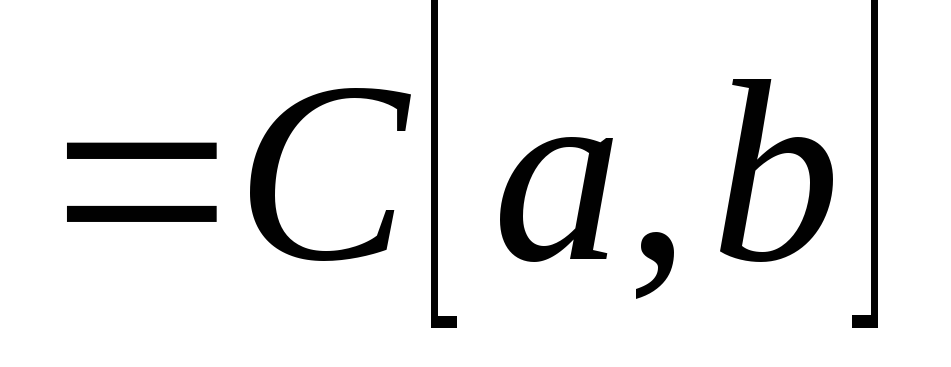1. . Для каждой непрерывной на 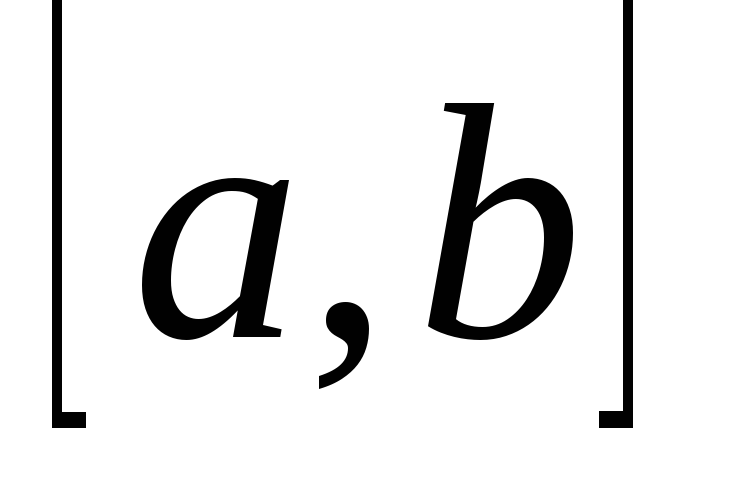функции 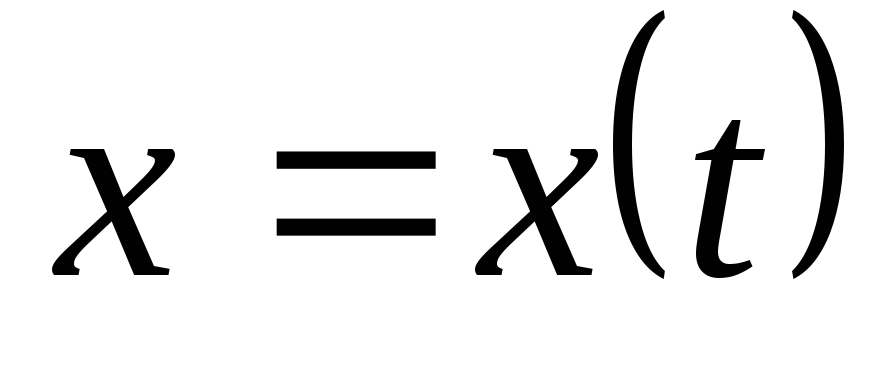положим .

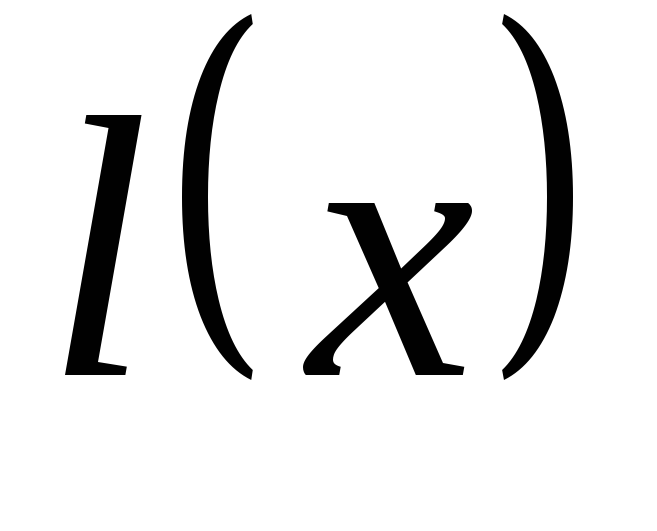
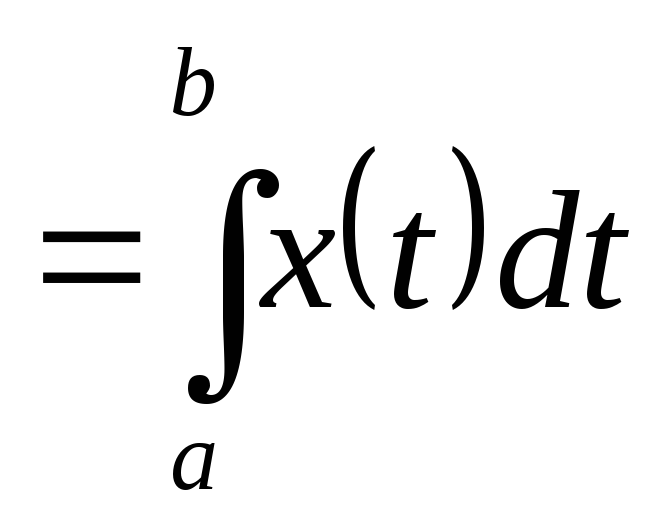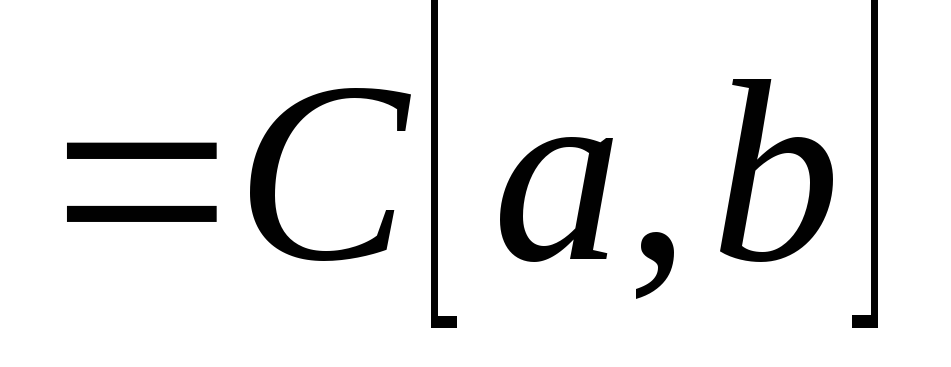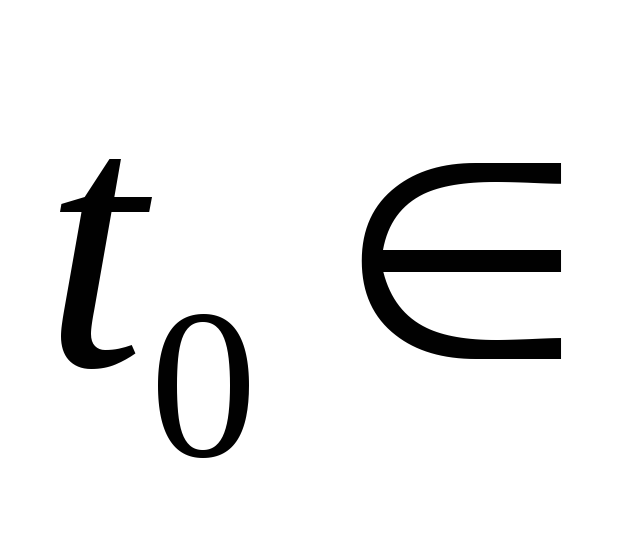
2. .Фиксируем 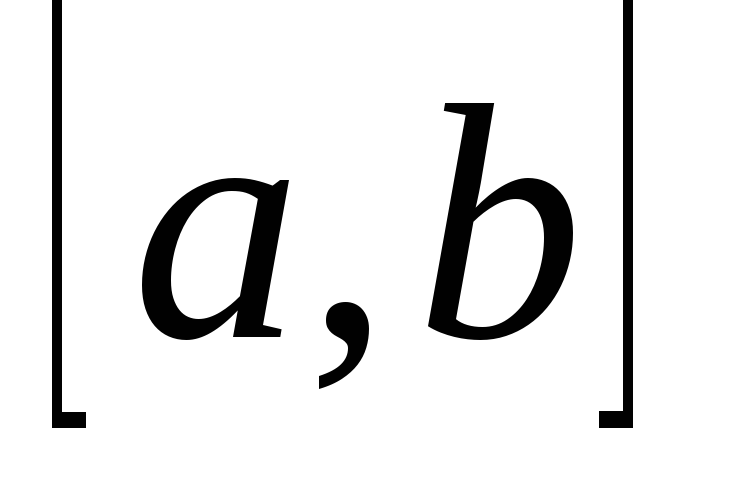и для каждой непрерывной на 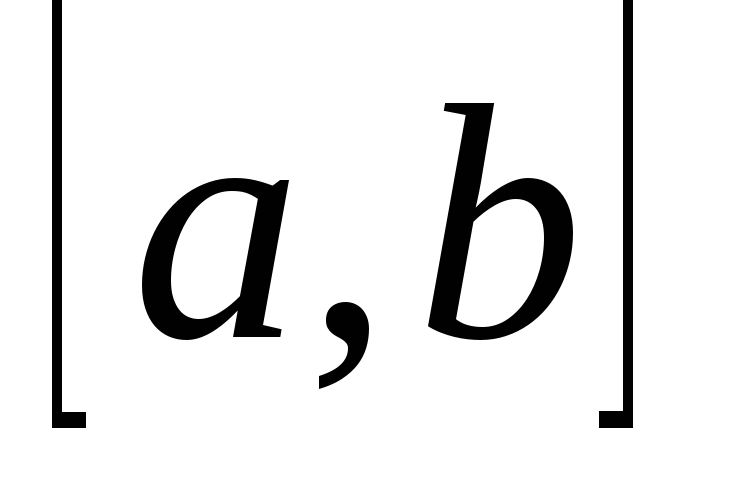функции 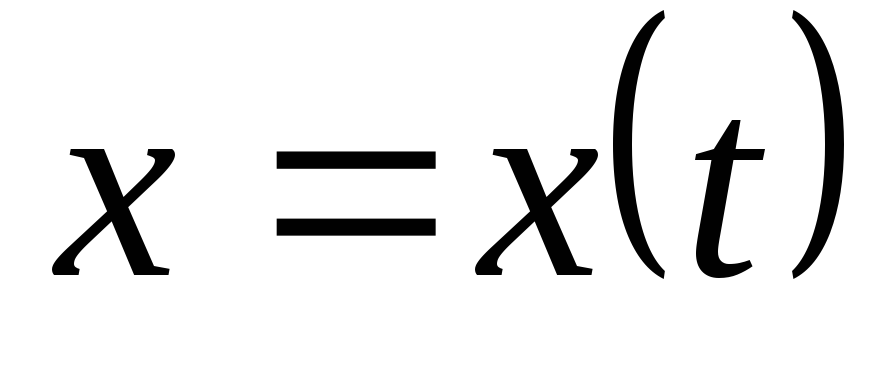положим .

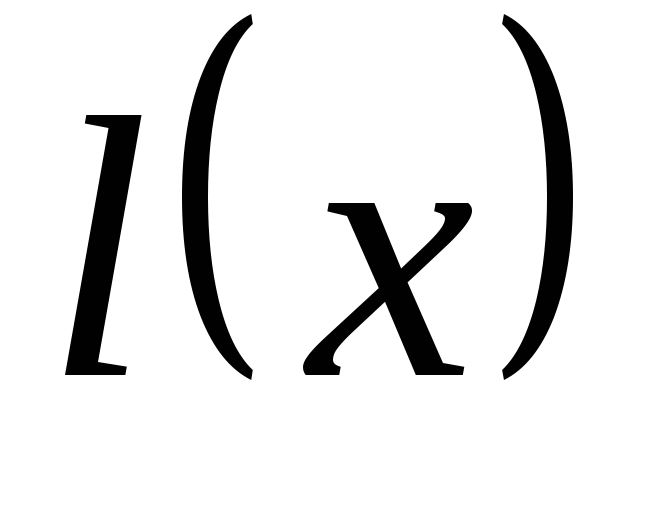
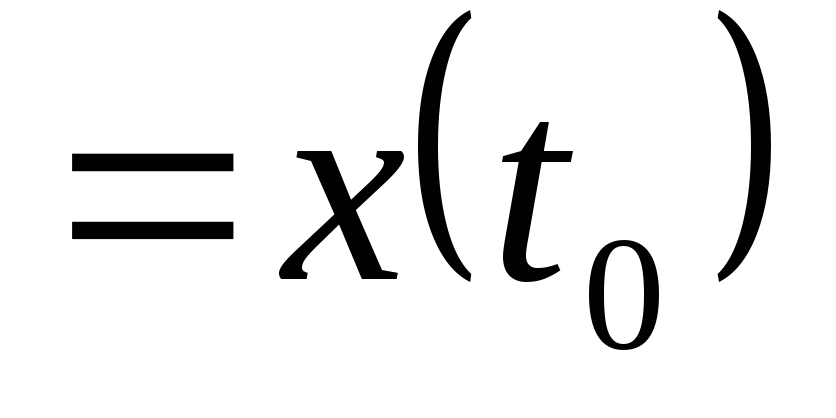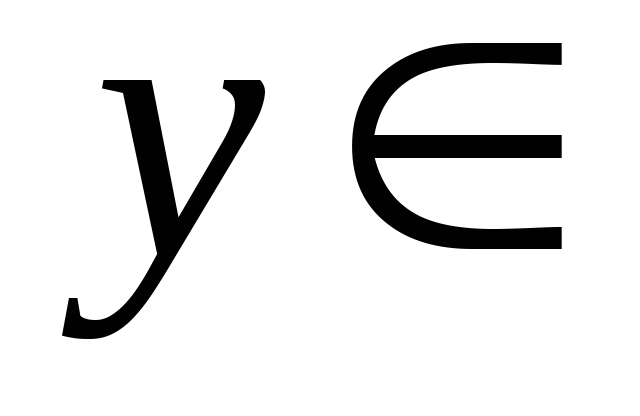
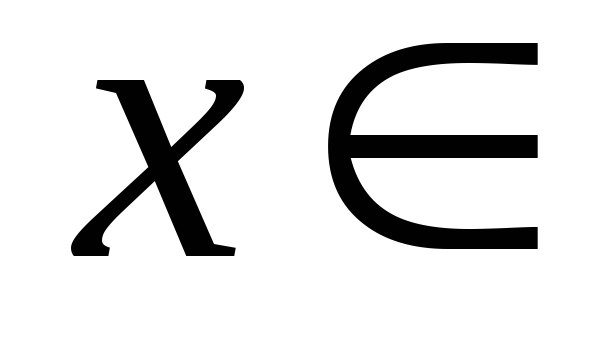
3. – евклидово пространство. Фиксируем элемент и для каждого положим .

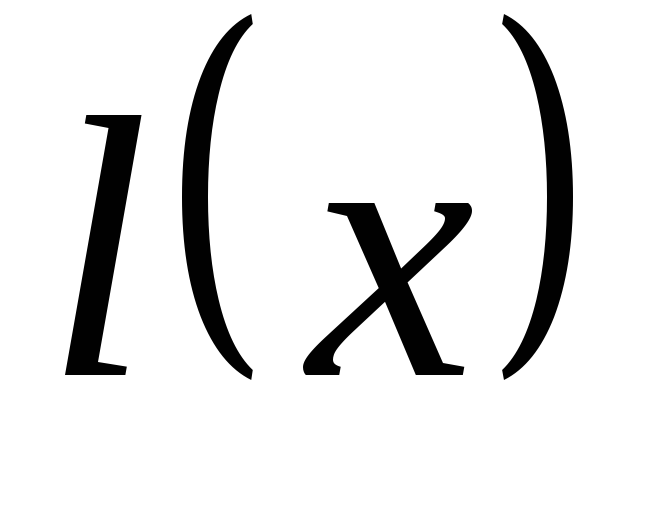
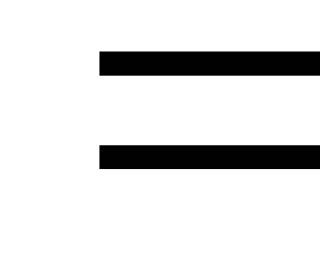
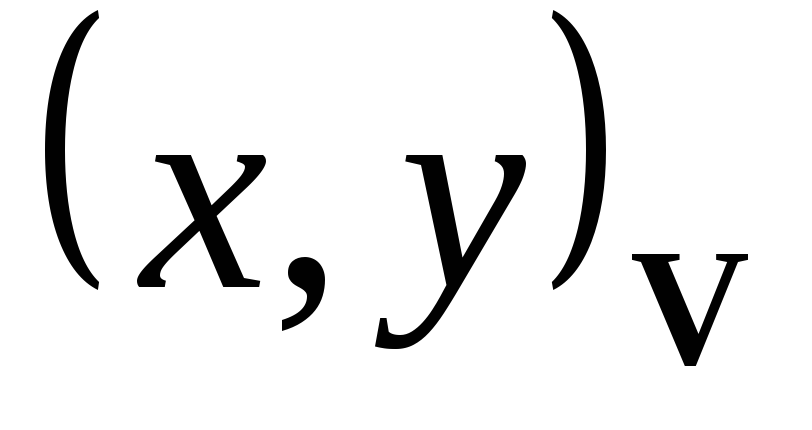Если и – базис в , то для любого и , где коэффициенты определяются выбором базиса.

Замечание. Обычно считают, что значения функционала должны определяться только самими элементами и не должны зависеть от выбора базиса. Если – базис в и , то можно, например, ввести функционал . Такой функционал обладает свойством линейности, но определяется не только элементами , но и выбором базиса: . Другой пример: – пространство многочленов степени не выше ; для фиксированного отрезка положим для любого . Этот линейный функционал не зависит от выбора базиса в . Далее будем рассматривать только линейные функционалы (формы), значения которых не зависят от выбранного в базиса.

Пусть и – два базиса в , связанные матрицей перехода : (напомним, что и мы рассматриваем как строки, состоящие из базисных элементов, – см. тему 2). Тогда из разложений имеем , где , . Введем вектор-столбец и матрицу-строку коэффициентов ; точно так же и . Тогда в матричных обозначениях . Нас сейчас интересует связь между и . Очевидно, для имеем 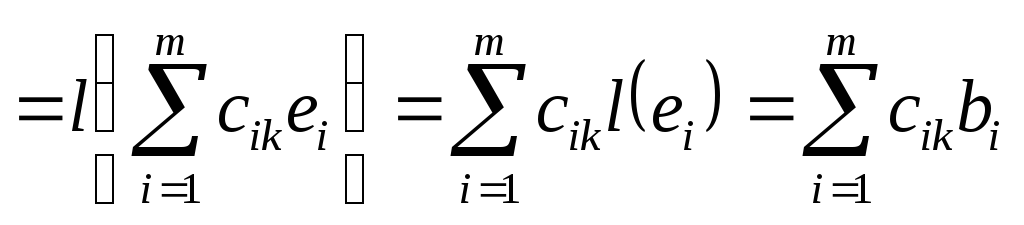. Этим доказана

Теорема 1. При замене базиса коэффициенты линейной формы преобразуются так же, как векторы базиса: .

Обозначим через множество всех линейных (и непрерывных!) функционалов, определенных на . Если линейное пространство задано над полем чисел , то будем умножать линейные функционалы из на числа и складывать такие функционалы: , ; при этом будут получаться новые линейные функционалы.

Теорема 2. является линейным пространством. Если , то и .

(Докажите самостоятельно, заметив, что является пространством линейных операторов : .)

Определение. Линейное пространство называется сопряженным к линейному пространству .

Теорема 3. (Геометрический смысл линейной формы.) Если , ≢, и , то множество является гиперплоскостью в линейном пространстве . Для любой гиперплоскости в пространстве найдется такая линейная форма , что данная гиперплоскость является геометрическим местом точек , на которых . Гиперплоскости, отвечающие различным значениям одной и той же линейной формы, параллельны. Гиперплоскость, на которой , проходит через начало координат.

(Докажите самостоятельно.)

Замечание. Если является евклидовым или унитарным пространством, то все определённые на линейные формы задаются при помощи скалярного произведения. Именно: для любой линейной формы существует, и притом единственный, элемент такой, что для всех .

Замечание о термине «форма». Многочлен называют однородным многочленом степени , если . Например, выражение является однородным многочленом степени 2 относительно переменных . Если в пространстве фиксирован базис, то линейный функционал является однородным многочленом первой степени относительно координат элементов в этом базисе. Однородные многочлены степени принято называть формами степени . При получаем линейные формы, при – квадратичные формы.