2. Самосопряженные операторы.

Операция сопряжения линейного оператора аналогична по смыслу операции сопряжения комплексного числа. Для -матрицы она означает . Среди всех комплексных чисел действительные числа характеризуются тем, что . Аналогом действительных чисел в пространстве операторов является важный класс самосопряженных операторов.

Определение. Оператор называют самосопряженным, если .

Всякое комплексное число представимо в виде , где и – действительные числа. Аналогичное представление имеет место и для линейных операторов.

Теорема 7. Пусть – конечномерное унитарное пространство. Всякий оператор может быть представлен в виде , где и –самосопряженные операторы. (Здесь – мнимая единица.)

Доказательство. Имеем тождество . Введем обозначения: , . По свойствам операции сопряжения имеем

,

.

Теорема 8. Пусть ,, , . Оператор является самосопряженным в том и только в том случае, если (такие операторы и называют перестановочными).

Доказательство. . Поэтому равенство выполнено в том и только в том случае, если .

Теорема 9. Пусть . Если , то для любого скалярное произведение является действительным числом.

Доказательство. .

Теорема 10. Все собственные значения самосопряженного оператора суть действительные числа.

Доказательство. Пусть – собственное значение оператора , т.е. существует такой вектор , что . Тогда . Поскольку и – действительные числа, то и – действительное число.

Теорема 11. Собственные векторы самосопряженного оператора, отвечающие различным его собственным значениям, ортогональны.

Доказательство. Пусть и , , где , , . Тогда и

. В силу имеем

. Поэтому . По условию теоремы , следовательно, .

Построим матрицу самосопряженного оператора. Для этого выберем в пространстве ортонормированный базис . В этом базисе матрицы и операторов и сопряжены друг другу. Тогда для оператора имеем ; такую матрицу называют самосопряженной. Если – евклидово пространство (), то матрица самосопряженного оператора удовлетворяет условию ; такую матрицу называют симметричной.

Теорема 12. Пусть . Оператор является самосопряженным в том и только в том случае, если в пространстве существует ортонормированный базис, в котором матрица этого оператора действительна и диагональна .

(Без доказательства. Доказательство см. в [3].)

Теорема 12 означает, что в некотором ортонормированном базисе матрица самосопряженного оператора имеет вид

,

где все действительны. При этом базис целиком состоит из собственных векторов оператора : , , (здесь не обязательно различны). Таким образом, жорданова форма матрицы самосопряженного оператора составлена из клеток , ; базис, в котором матрица этого оператора имеет жорданову каноническую форму, является ортонормированным и состоит из собственных векторов.

Поскольку самосопряженные операторы являются аналогами действительных чисел, хотелось бы выделить среди них в некотором смысле положительные операторы.

Определение. Самосопряженный оператор называют неотрицательным, если для любого выполнено неравенство (обозначение: ). Самосопряженный оператор называют строго положительным (или положительно определенным), если и только для (обозначение: ).

Данное определение является корректным, поскольку для оператора число действительно при любом .

Утверждение. Если оператор , то все его собственные значения . Если оператор , то все его собственные значения .

Доказательство. По теореме 12 у самосопряженного оператора имеется ортонормированный базис , состоящий из собственных векторов. Поэтому , . Для неотрицательного оператора все , т.е. все . Для строго положительного оператора все , т.е. все .

Самосопряженный оператор, удовлетворяющий какому-либо из условий , (т.е. ), , (т.е. ), называют знакоопределенным. Очевидно, что не все самосопряженные операторы знакоопределенны: если у оператора имеются собственные значения разных знаков, то он не является знакоопределенным.

Если и –самосопряженные операторы, и , то пишут ; если , то пишут . Не всякие самосопряженные операторы и допускают сравнение в указанном смысле: может оказаться, что не является знакоопределенным.

Пример. Пусть – ортонормированный базис, и , . Тогда , . Но , т.е. оператор не является знакоопределенным.

Если , то для любого натурального числа можно ввести понятие корня -ой степени из оператора . Под корнем -ой степени из оператора понимают такой оператор , что . По теореме 12 в некотором ортонормированном базисе матрица оператора имеет каноническую форму

,

где все действительны и неотрицательны. Положим в том же базисе

.

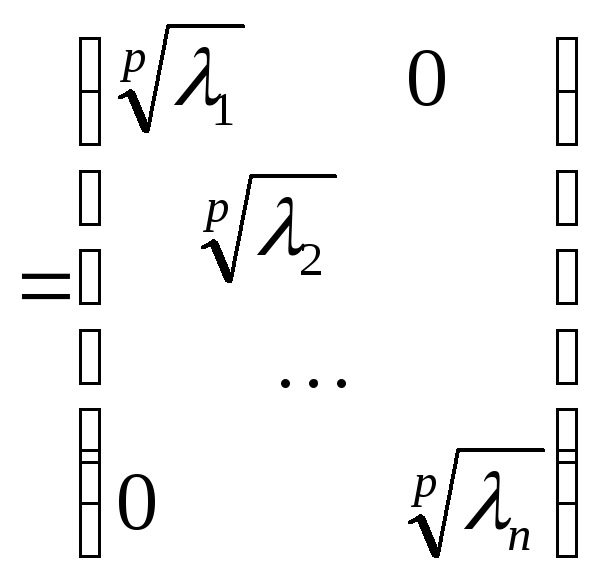Очевидно, . В силу взаимно однозначного соответствия между операторами и их матрицами в фиксированном базисе мы получили требуемый оператор .

Утверждение. Если , то оператор невырожденный, и .

(Докажите самостоятельно. Каковы в этом случае собственные значения оператора ?)