Тема 8. Линейные операторы в евклидовых и в унитарных пространствах.

1. Сопряженные операторы.

Новые свойства оператора появляются, если в и в ввести скалярные произведения. В случаях, когда и – евклидовы линейные пространства (), или когда и – унитарные пространства (), наиболее важными свойствами линейного оператора оказываются те, которые связаны с понятием ортогональности. Основную роль при изучении этих свойств будет играть оператор, сопряженный к данному оператору.

Определение. Пусть и – конечномерные евклидовы или унитарные пространства, . Отображение

: называют оператором, сопряженным к оператору , если для любых элементов , выполнено равенство .

Заметьте, что в определении ничего не говорится о линейности ; линейность надо еще доказать.

Теорема 1. Пусть , тогда существует оператор , сопряженный к , и притом только один. является линейным оператором: .

Доказательство. Выберем в пространстве произвольный ортонормированный базис . Разложение любого элемента по этому базису имеет вид

, (1)

где – коэффициенты Фурье элемента (см. тему 4).

Пусть существует оператор , сопряженный к оператору ; докажем, что единственный. Для любого его образ при отображении является элементом пространства : . Поэтому для выполнено разложение (1): . Пользуясь аксиомами скалярного произведения и определением сопряженного оператора, получаем

. (2)

(Черта в (2) означает комплексное сопряжение. Равенство (2) записано для случая унитарных пространств и . Если и – евклидовы пространства, то на операции комплексного сопряжения в (2) можно не обращать внимания.) Разложение элемента по базису единственно. Поэтому, если для оператора существует , то определен единственным образом формулой (2).

Примем формулу (2) за определение действия оператора в базисе пространства . Докажем, что так определенный оператор : удовлетворяет условию для любых , . В силу линейности оператора имеем (см. (1))

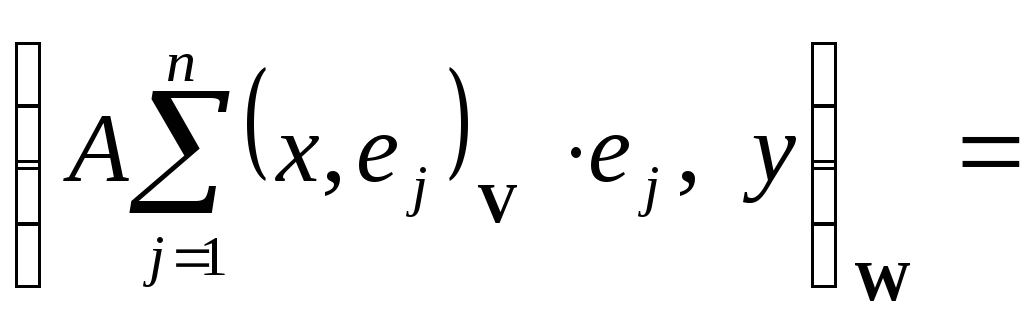
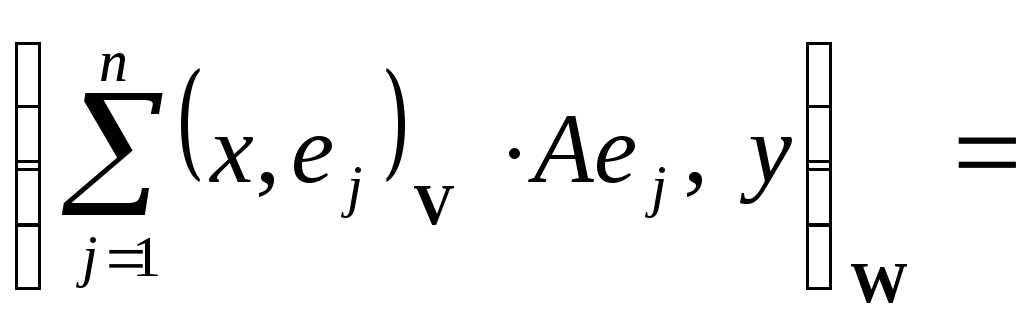
. (3)

Из задания оператора формулой (2) и в силу ортонормированности базиса имеем

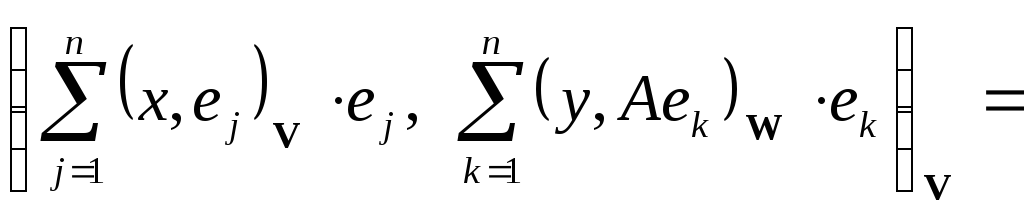
. (4)

Сравнивая (3) и (4), получаем, что заданный формулой (2) оператор удовлетворяет определению сопряженного оператора.

Докажем, что построенный оператор является линейным. Для любых элементов и и для любых чисел имеем

. (5)

С другой стороны, по определению сопряженного оператора

. (6)

Обозначим . Мы только что доказали, что для любого элемента выполнено (вычесть из (5) равенство (6)). В частности, при имеем , Отсюда .

Теорема 2. (Свойства операции сопряжения.)

; ; ;

– в случае унитарных пространств ;

– в случае евклидовых пространств .

(Докажите самостоятельно, исходя из определения сопряженного оператора.)

Теорема 3. Пусть , и . Пусть существует обратный к оператор . Тогда и у оператора имеется обратный оператор , причем .

Доказательство. Докажем сначала, что если – невырожденный оператор, то и – невырожденный. Пусть . По формуле (2) получаем разложение нулевого элемента по ортонормированному базису : . Отсюда для всех . В силу невырожденности оператора образы базисных векторов образуют базис в . Тогда элемент оказывается ортогональным ко всем базисным векторам; поэтому . Итак, если оператор невырожденный, то , т.е. и оператор невырожденный.

Из невырожденности операторов и вытекает, что для любого существует единственный элемент , для которого , и что для любого существует единственный элемент , для которого . Поэтому для любого имеем . Отсюда для любого получаем , а это и означает, что .

Построим теперь матрицы операторов и . Выберем в пространстве ортонормированный базис , а в пространстве – ортонормированный базис . Если , то будем считать совпадающими базисы и . Пусть оператор в паре базисов и имеет матрицу ; это значит, что . Поскольку – ортонормированный базис, коэффициенты разложения элемента по базису являются его коэффициентами Фурье:

, . (7)

Пусть оператор в паре базисов и имеет матрицу ; это значит, что . Поскольку – ортонормированный базис, коэффициенты разложения элемента по базису являются его коэффициентами Фурье:

, . (8)

Сравним (7) и (8), пользуясь определением сопряженного оператора:

, .

Определение. Пусть матрица . Матрицей , сопряженной к матрице , называют матрицу : (черта означает комплексное сопряжение всех элементов матрицы).

Очевидно, что если матрицу транспонировать и взять комплексное сопряжение всех ее элементов, то ранг матрицы не изменится. Напомним, что ранг матрицы линейного оператора не зависит от выбора базисов. Тем самым доказана

Теорема 4. В любых ортонормированных базисах и сопряженным операторам и соответствуют сопряженные матрицы и . Ранги операторов и совпадают: . Если , то .

Теорема 5. ; .

Доказательство. Пусть и – конечномерные пространства, . Пусть , т.е. . Тогда для любого элемента имеем . В силу произвольности и это означает, что

. (9)

Вспоминая, что , точно так же получаем

. (10)

По теореме 6 темы 6 имеем , . По только что доказанной теореме 4 . Поэтому , т.е. из (9) получаем

;

и точно так же из равенства и из (10) получаем

.

(Символ означает ортогональную сумму подпространств; – см. тему 4.)

Теорема 6. Пусть . Если подпространство пространства инвариантно относительно оператора , то его ортогональное дополнение инвариантно относительно оператора .

Доказательство. Пусть , тогда и . Если , то . Но тогда и . В силу произвольности это означает, что , т.е. .