Тема 3. Задачи о минимальном остове.
3.1 Деревья.
3.1 Построение минимального остовного дерева (алгоритм Краскала).
3.1 Деревья.
Втречаются в областях, не имеющих к теории графов прямого отношения. Деревья открывали независимо несколько раз.
Кирхгоф еще в прошлом веке ввел деревья и применил к исследованию электрических цепей. А Кэли использовал их в химии для описания структуры органических соединений. Тогда же деревья были введены и исследованы К. Жорданом, как чисто математические объекты.
Деревом называется простой связный граф, не содержащий циклов. Две вершины такого графа связаны только одной цепью. Деревья определялись по-разному.
Теорема: для графа G с N вершинами и R ребрами следующие утверждения эквивалентны.
G- дерево;
G- связный граф, R=N-1;
G- ациклический граф, R=N-1;
Любые две несовпадающие вершины графа G соединяет простая единственная цепь;
G-ациклический граф, такой что, если какую либо пару его несмежных вершин соединить ребром, то граф будет содержать ровно один цикл.
Дерево имеющее N вершин, всегда содержит R=N-1ребро, т.е минимальное количество ребер для того, чтобы граф был связным.
Если из дерева удалить хотя бы одно ребро, то граф становится несвязным, он распадается на компоненты, которые могут быть так же деревьями или отдельными вершинами. При добавлении в дерево ребра образуется цикл.
Несвязный граф, компонентами которых являются деревья, называется лесом.
Среди различных деревьев особо выделяют последовательное дерево (рис.3а), представляющее простую цепь и звездное дерево (рис. 3б), в котором одна из вершин смежная со всеми остальными вершинами.
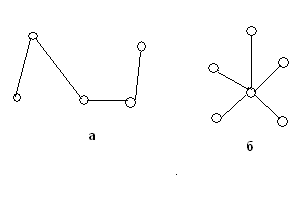
Рисунок 3 .
Если в каждой компоненте связности графа G есть дерево H , то H называется остовом графа G.
Если в связном графе G последовательно удалять ребра, входящие в какой либо цикл, то в конце концов получится дерево, содержащее
все вершины, исходного графа. Такое дерево, называется остовом графа G. Если граф не связный, то его остовом является лес, состоящий из деревьев, является остовами
компонента связности графа.
Число ребер произвольного графа G, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно V(G)=R-N+r, где r- число компонент связности G.
Число V(G)=R-N+r называется цикломатическим числом графа G и определяет меру связности графа.
Для леса V=0, для связного дерева V(H)=0, так как R=N-1,r=1 (V=N-1-N+1).
Граф имеет единственный цикл тогда и только тогда, когда V(G)=1. Любой граф, в котором число ребер не меньше чем число вершин, содержит цикл. Естественно возникает вопрос: как много остовов в графе? Для полного графа число остовов равно NN-2 (N-число вершин). Теорема Кирхгофа (1847г.). Число остовов в связном графе G порядка N≥2 равно алгебраическому дополнению любого элемента матрицы Кирхгофа B(G)=I*IT.
В приложениях часто бывает так, что одна из вершин дерева, а так же ее взаимосвязи с остальными вершинами имеют особое значение. В этом случае удобно рассматривать корневые деревья. В неориентированном случае в качестве корня дерева может рассматриваться любая вершина. Тогда соседние с ней вершины называются вершинами первого уровня (яруса), соседние с ним (отличные от корня) вершинами второго уровня и т.д. коневое дерево удобно выполнять в виде укладки, располагая вершины одного уровня на одной высоте. Если в корневом дереве выбрать некоторую вершину то множество всех вершин, связанных с корнем цепями проходящими через V, называется ветвью для V в корневом дереве. Ветвь- это подграф корневого дерева, который сам является корневым деревом с корнем в V.
В случае орграфа вводится понятие ориентированного дерева. Если все ребра графа направлены в сторону вершины более высокого уровня, то дерево называется ориентированным. В каждую вершину ориентированного дерева входит только одно ребро ( или не одного, если это корень). Если все ребра графа направлены к корню, то дерево называется схемой сборки.