Конечно-разностная аппроксимация.
Большинство задач в физике и технике приводят к линейным и нелинейным дифференциальным уравнениям в частных производных. Одним из методов (иногда единственным) решения таких уравнений является метод конечных разностей. При его использовании предполагается, что решение исходных задачи существует и имеет нужное число производных, обеспечивающих максимальный порядок аппроксимации. Чтобы составить разностную схему, приближено описывающую данное дифференциальное уравнение необходимо выполнить:
заменить область непрерывного изменения аргумента областью его дискретного изменения.
заменить дифференциальный оператор некоторым разностным аналогом и сформулировать соответствующее выражение для краевых и начальных условий.
Из-за континуальности области определения дифференциального уравнения для ее аппроксимации берется конечное число точек, решение ищется в этих точках.
Для нахождения значений в промежуточных точках могут использоваться интерполяционные многочлены. Множество выбранных точек – сетка, сами точки – узлы. Формула, определённая в узлах сетки, называется сеточной. Свойство решения и его точность зависят от выбора сетки и выбранной схемы аппроксимации. Таким образом, вместо функции непрерывного аргумента y(x), рассматривается функция дискретного аргумента yh(xi), где h – шаг сетки, влияющей на значение функции. Сетка может быть равномерной и неравномерной. Для разностной аппроксимации необходимо предварительно выбрать шаблон, т.е. множество точек сетки, окружающий рассматриваемую точку x.
Оператор первого
порядка:
Производную в точке x можно рассматривать в виде шага вперёд или назад
Можно также взять линейную комбинацию этих выражений
При
Для выбора аппроксимации нужно учитывать ошибку (меньшая ошибка), т.е.
Разложим v(x) по формуле Тейлора:
Подставляя это
выражения в формулы
, получим:
или,
вернее,
Точнее, чем
Если взять пятиточечный шаблон, то
Точность аппроксимации 0(h4).
Аппроксимация функции второй производной:
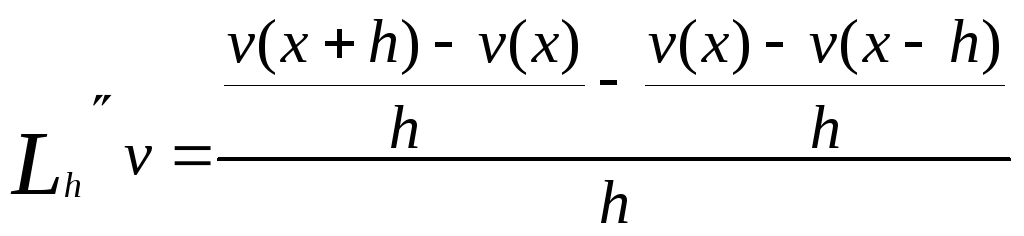
При разложении в ряд Тейлора получаем погрешность
Для пятиточечного шаблона:
Для третьей производной при пятиточечном шаблоне:
Рассматривалась равномерная сетка. Хорошо, если края сетки совпадают с границами области определения.
Целесообразно, чтобы для конечно-разностной аппроксимации производных использовались формулы, дающие одинаковый уровень погрешности (например, o(h2)).
Приближение функции многочленами
В Rn
– пространстве( n-мерное пространство
точек
с
координатами x1,
x2,
… xn)
заданы точки
и значения
функции
в
этих точках.
Нужно найти
аналитически функцию «U», которую можно
представить в виде линейных комбинаций
заданных функций
так, чтобы она в заданных точках
наименьшим
отклонялась от значений
,
чтобы дефекты
[в
т.
]были
минимальными.
Для этого необходимо, найти ak:
1 случай:
s=m, тогда если
, т.е. матрица, коэффициенты которой
есть значения функций
в соответствующих точках
, то можно
получить дефекты
.
Коэффициенты ak
находятся из условия
путём решения СЛАУ. В этом случае
выражение
интерпретирует значение
.
Таким образом, при s=m, мы имеем задачу интерполяции.
2 случай:
s<m, следовательно относится к задаче аппроксимации.
s>m
интереса не представляет, потому что
некоторые функции
будут
зависеть от других функций
.
Т.е. задача аппроксимации f(x) сводится к нахождению y(x):
Здесь
считаются заданными, а коэффициенты ak
ищутся так, чтобы расстояние ||f-g||
было минимальным.
В качестве такого расстояния можно рассматривать:
Для дискретного
случая
В качестве d можно
брать
.
Такая аппроксимация называется чебышевской, или T-аппроксимацией, которая часто применяется для решения дифференциальных уравнений с краевыми условиями.
Случаи относятся к линейной аппроксимации.
Используют также и так называемую рациональную аппроксимацию:
x – набор x1…..x2
- заданные функции
- искомые постоянные
коэффициенты
Также аппроксимации используются для вычисления на ЭВМ функций Бесселя (напр.), которые применяются для расчетов пластин и оболочек; tg(x) и т.п.
При рациональной аппроксимации с заданной степенью точности часто требуется меньше коэффициентов, чем при линейной.
[-1;1]
Т-аппр:
на
том же отрезке
Для n=3
n=4
Задание различных норм точности аппроксимации может существенно влиять на мин. решение.
Для
с
помощью линейной функции y=ax + b на отрезке
[0;1] по классическому МНК коэффициенты
a и b находятся из условия
МНК:
;
Т-ап:
;
При линейной
аппроксимации функции
в качестве функции
могут выбираться как обычная степенная
функция вида
,
так и специальные функции, в частности
ортогональные многочлены, т.е.
u
Если bi=1, то ортонормированные многочлены.
В качестве ортогональных многочленов часто выбирают
а). Лежандра:
[-1;1]
i - № многочлена
при
- реккурентная
формула
б). Чебышева:
на [-1;1]
T0(x)=1 ; Tn(-1)=(-1)n ; T1(x)=x
0
Рекуррентная формула:
Известна теорема,
что в лин. нормированном пространстве
R
для заданных элементов f(x),
всегда
min решение.
Для одномерного пространства чебышевское приближение лучше МНК.
Для многомерного пр-ва сказанное выше неочевидно, поэтому используют МНК.
Пусть s=m и в [a;b]
заданы m+1 опорные точки
, а также значения f(x) в опорных точках.
Требуется найти
Im(x)
степени не более m
такой, что Im(xj)
= f(xj)
.
Всегда имеется только один интерполяционный многочлен, но однозначно определённый многочлен может быть представлен в различных видах или формах.
Форма Ланганжа:
,
где
Здесь степень
не больше “m”
и
,
при
поэтому
.
Форма Ньютона
,
где
,
j=1, m
- разделённая
разность
;
