I метод Ляпунова.

Т/1

Состояние равновесия [х₀=0] дифференциального уравнения

, где f(x)=0

[х – некоторая обобщённая координата]

является асимптотически устойчивым, если состояние равновесия соответствует свободной линейной стационарной системы , где А=||_0, явл-ся асимптотически устойчивым.

Т/2

Состояние равновесия Ǿ дифференциального уравнения , где f(0)=0, является неустойчивым.

Если состояние равновесия Ǿ соответствует свободной линейной стационарной системы , где А=||_0, является неустойчивым.

Пр/1

В соответствии с Т1 продифференцированные правые части по х и y

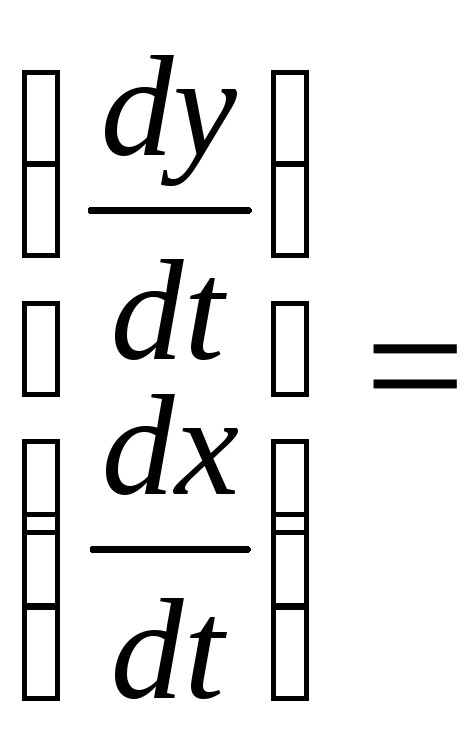
Ax=||х, где - собственные числа, которые находятся из уравнения:

(1-)²+1=0

(1-)_1;2=±i

_1,2=1±I a±i

e^at (sin b + cos b)

∞ ≤1

неустойчивая система (при а>0)

устойчивая система (t→∞; a<0 e^at→0)

Так как a=1>0, то система неустойчива.

Пр/2

<0 система устойчива.

Пр/3

Упругие колебания маятника с учётом сил трения или сопротивления среды имеют вид:

b – коэффициент затухания

с – постоянная, зависящая от тяжести и длины маятника

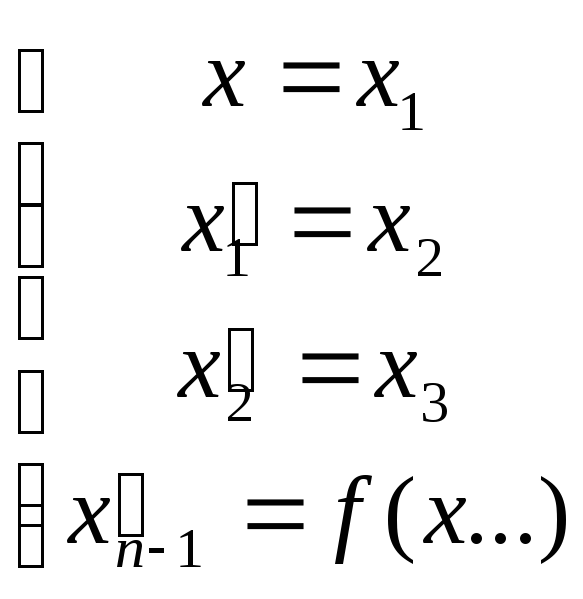
Для n=3:

x_2,0=0; x_1,0=0

1. b>0

2. b<0

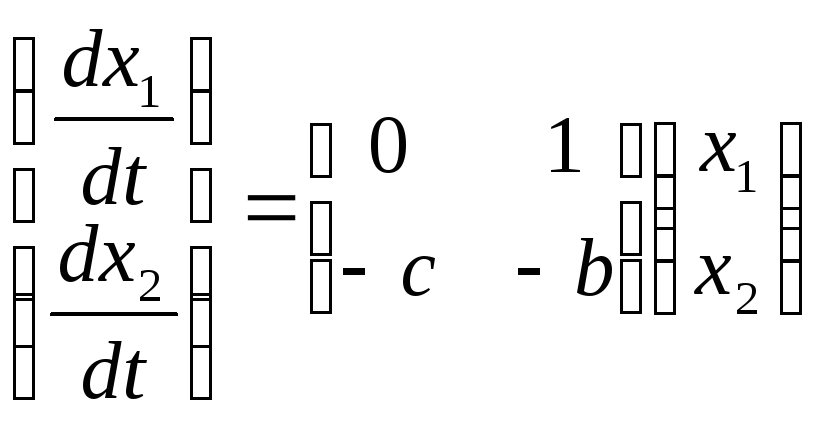
3. b=0

b>0 → устойчива

b<0 → неустойчива

b=0 → мнимый корень → ответ неясен

II метод Ляпунова.

Т/1

Если дифференцируемая функция v(x_i) i=1…n, называемая функцией Ляпунова и удовлетворяющая в окрестности начала координат условиям:

1. v(x_i) ≥ 0, v(x_i)=0 при x_i=0 i=1..n

2. , при t>t₀ в силу уравнения (*),

то точка покоя x_i =0 i=1..n системы устойчива.

Не выходим за пределы .

Т/2

Если дифф. Функция Ляпунова v(x_i) i=1…n, удовлетворяющая условиям

1. v(x_i)=0 при x_i=0 (v(x_i)>0, если x_i≠0) i=1…n

2. в поле сколь угодно малой окружности начала координат

<0, где - const,

то точка покоя x_i=0 i=1…n системы асимптотически устойчива.

Пр/4

± ответ неясен

v=3x₁²+4x₂²

v(x_1, x₂)≥0

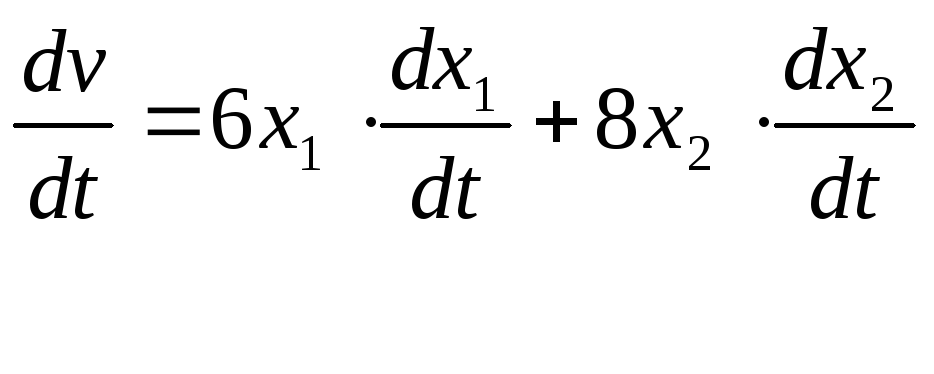
v(0_, 0)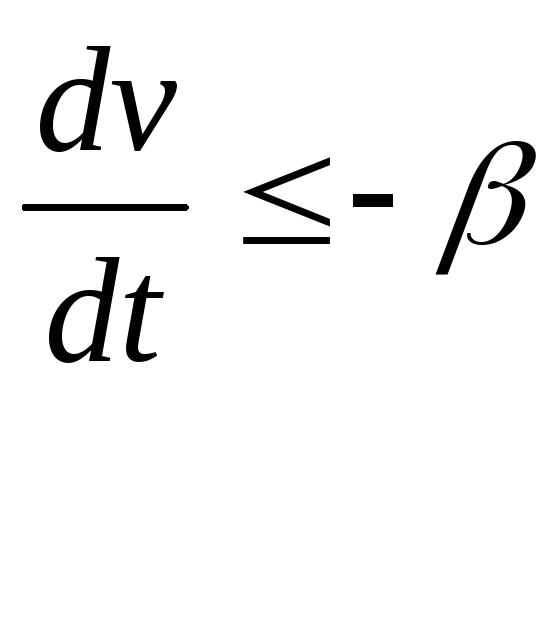=0

<0

Значит, (0,0) – асимптотически устойчива (по Т2)

Пр/5

1)

2)

<0 точка покоя асимптотически устойчива

Если для некоторой функции v условия теорем не выполнены, то это не означает, что система не устойчива, т.к. может быть неправильно выбрана сама функция v.

Если исследуемая система подвержена малым возмущениям (кратковременным), то её можно заменить возмущённой системой на интервале вида

и мало, а при t>t₁ возвращаемся к прежней системе.

При асимптотической устойчивости поле траекторий стремится к нулю.

При нелинейных членах или погрешностях (например, машинные округления.) траектории смещаются, и если при t→∞ эти траектории стремятся к 0, то в начале координат возникает устойчивый или неустойчивый фокус.

--фокус

Практически все задачи строительной механики можно представить следующим образом:

Пусть имеется некое внешнее воздействие и поведение системы . Математическая природа элементов обоих пространств может быть произвольной (числа, функции, векторы, тензоры – обобщение матриц..). Структура и свойства системы характеризуются оператором Н таким образом, что u=H*q.

q – воздействия (ветер, землетрясение…)

u – перемещение, напряжение, деформация

H – теория упругости, пластичности, механики твёрдого тела, динамики, а также граничные и начальные условия

Систему можно изобразить и так: L*u=q

u L q

P

q H u P – возмущения

Модель «Сила - перемещение»

Иногда оператор М может зависеть от параметра λ (напр. время), тогда система выглядит так:

P т.е. мы имеем обратную связь, поэтому эта система

автоматического управнения

q H u

L λ

L*u=q. Введем некоторое пространство V для описания качества системы. Время t Є Т может играть роль параметра. При изменении t одно состояние системы переходит в другое, т.е. u=u(t). последовательность изменения состояний, или эволюция состояний u(t), представляется виде некоторых траекторий. Каждой траектории u=u(t) соответствует траектория v(t) Є V в пространстве качества. Связь между ними можно описать оператором М. V=M*u. множество состояний системы, допустимых с точки зрения качества, образуют в пространстве V область допустимых состояний Ώo. Граница Г области допустимых состояний соответствует предельным состояниям. Если V Є Ώo, то параметры качества сохраняются в установленных пределах. Пересечение границы Г траекторией v(t) соответствует отказу системы (напр. потеря устойчивости, превышение заданной стоимости). Если система q Є Q дискретна, то Q, V, U – евклидовы пространства.