Метод статистических испытаний (метод монте-карло)

Состоит в использовании связи между вероятностными характеристиками и аналитическими вычислительными задачами. Вместо вычисления ряда сложных аналитических выражений можно экспериментально определить значения соответствующих вероятностей или математических выражений.

П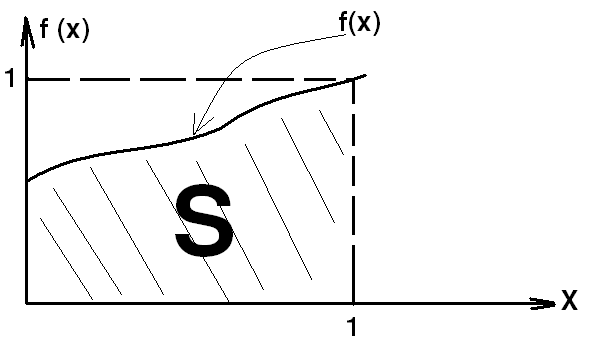ример:

Вычислить интеграл I=

Q f(x) 1

Пусть квадрат 0 х 1, 0 у 1 случайно попадают точки, координаты которых независимы и равномерно распределены в интервале (0, 1). Какова вероятность, что эти точки попадают в область по кривой?

Очевидно, что эта вероятность Р численно равна S.

Пусть наугад взятая точка характеризуется 0 ξ, h 1 координатами (ξ, h). Если имеется некоторый способ получения независимых равномерно распределенных величин ξ и h, то можно покрыть весь квадрат , тогда для (ξ1, h1) проверяем условие h1 f(x), т.е. находится на кривой f(x) или под ней. Если условие выполнено, то точка попала в S. Аналогично проверяется условие попадания для остальных точек. Затем подсчитываем число пар (m), попавших в S, тогда в силу закона больших чисел :

дробь р (где n – общее число точек) близка вероятности попадания точки в область S. Эта величина есть приближенное значение искомого интеграла.

Чем больше точек испытаний, тем точнее будет результат. Для оценки кол-ва точек (N), необходимого для получения результата с точностью ε², используют выражение :

N= =

Эта оценка для доверительной вероятности равна 0,997. в формуле «р» характеризует вероятность, что оценка математического ожидания определенной величины не превысит ошибки ε. D(ξ) – дисперсия моделируемой величины ξ. Таким образом, увеличение точности в 10 раз требует увеличение числа испытаний в 100 раз. В практических задачах метод статических испытаний дает точность 0,01-0,001 от максимального значения , количество случайных чисел – 100тыс и более. Однако этот метод хорошо приспособлен к многомерным задачам и практически единственным в этом случае.

Задачи, решаемые методом Монте-Карло, делятся на 2 группы:

допускающие формулируемые

аналитическую в терминах случайных

формулировку процессов

(1) (2)

(1) Решение системы линейных уравнений, краевых задач, многомерные интегралы

(2) Исследование процессов массового обслуживания, системы управления со случайными величинами входов, задачи моделирования различных самообучающихся систем.

Для реализации метода Монте-Карло необходимы случайные числа. Обычно берут совокупность случайных чисел с равномерным распределением на промежутке [0,1]

Равномерное распределение случайной величины h будет тогда, когда ее функция

плотности f(y): f(y) = {

ф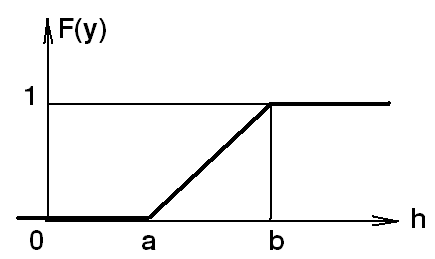ункция распределения случайной величины F(y)={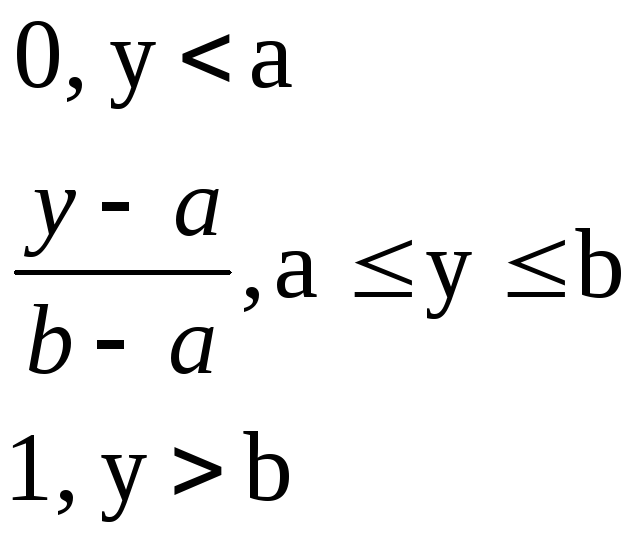

Математическое ожидание М:

М(h)=(a+b)/2

; дисперсия =

Случайные величины можно получать двумя способами:

1)генерирование с помощью спецприставки к ЭВМ (радиоактивное излучение)

2)алгоритмически

Однако во втором случае будут получаться псевдослучайные числа, т.к. разрядность ЭВМ мала.

Датчики случайных чисел должны быть проверены, должно быть установлено допустимое кол-во случайных чисел в последовательности, после чего она может вырождаться за счет повторения последовательности.

Иногда требуется получить последовательность случайных чисел с заданным законом распределения на основе последовательности случайных чисел с равномерным законом распределения. Известно, что если система имеет плотность распределения f(x), то распределение случайной величины h= является равномерным в [0,1]. Поэтому процедура преобразования равномерно распределена в интервале [0,1] случайных чисел R в случайные числа u c заданным законом распределения из формулы f(x)= λe следует:

1- e= R

х=-

пусть требуется получить последовательность случайных чисел uс нормальным законом распределения (математическое ожидание a, среднее квадратичное отклонение )

f(x)=

Если взять случайно равномерно распределенные числа ξ с математическим ожиданием а и среднеквадратическим отклонением , то ξ= ξ+….+ ξn будет асимптотически нормально а=n*а ;

Уже при n = 8 — 12 получается близкое к нормальному распределение.

Решение СЛАУ при помощи M – R.

i=1….n

V(x)= 0 < =1….n

ع

V(x) – n-мерный эллипс

V

х- образуют искомое решение и являются координатами центра симметрии этого эллипса.

Погрузим этот эллипс на параллелепипед такой, что

Образуем последовательность случайных векторов

i=1….N попарно независимы и равномерно распределены каждая на своем отрезке [A;B] , l=1…n

случайное число i-ого испытания для l-ого параметра

М - кол-во случайных векторов, удовлетворяющих соотношению V, т.е. попавших в эллипсоид (в т.ч. граница)

Частота М/N сходится по вероятности к отношению Vэ/Vп, где Vэ и Vп – объём эллипсоида и параллелепипеда соответственно.

Если =, то , т.е. так можно вычислить координаты центра симметрии эллипсоида, при этом , где D – дисперсия

Были представлены методы определения коэффициентов регрессии (r), коэффициент корреляции (h). Однако точность и достоверность этих величин неизвестны из-за того, вычислены для выборки, а не ген. совокупности данных. Информацию о точности и достоверности указанных величин доставляют доверительные оценки (доверительные границы).

П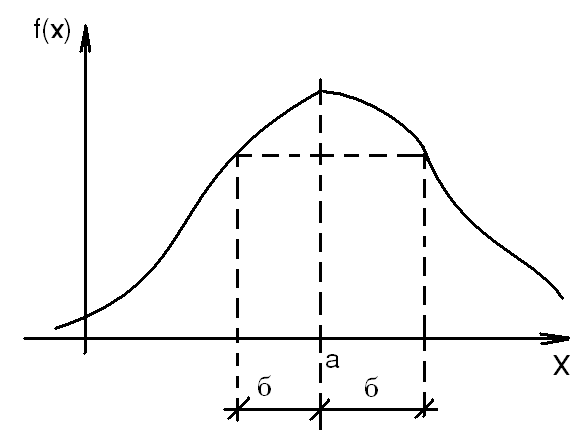усть - некоторая выборка из ген. совокупности с признаком Х, распределение которой зависит от параметра Х, а Г(х) есть вероятность Р(-Г(х)<<Г(х))=l-, тогда (-Г,Г) – доверительная оценка параметра с мерой надежности 1-, т.е. (-Г,Г) включает истинный параметр , с вероятностью 1-.

Пусть - выборка из независимых случайных величин б – расстояние от а до точки перегиба кривой, которая симметрична относительно точки а.

Рассмотрим функцию выборки

Распределение этой величины называется ХИ-квадрат распределения с n степенями свободы, равным числу опытов, или мощности выборки.

Если Т=Х/У (Х,У - независимы), где ХN(x,0,1) и У=, то распределение Т называется t-распределением или распределением Стьюдента.

² распределение в зависимости от n и вероятности

t – распределение, зависящее от числа n и вероятности , или t(m)

Оценим значимость (точность и достоверность) коэффициента корреляции. Для этого определяют фактическое и теоретическое значение критерия Стьюдента.

Для фактического значения критерия коэффициента корреляции:

или

(выборка) (регр. коэффициент)

корреляции

теоретическое значение критерия Стьюдента определяется по специальным таблицам для заданно значения доверительной вероятности р=1- и известного значения критерия Стьюдента.

Пусть Y, X, n = 7, r = 0,86 Р = 0,95

=0,05

t=2,365; коэффициент корреляции является существенным, а связь между Y и Х достоверной.

y= 0,09 + 0,24 * х

а а

Для линейной зависимости одной переменной есть формулы оценки случайных погрешностей коэффициентов аи а , а также оценки значимости этих коэффициентов. Для общего случая таких формул нет или они очень сложные.

Для определения доверительных границ уравнения регрессии существуют формулы:

у= , где ;

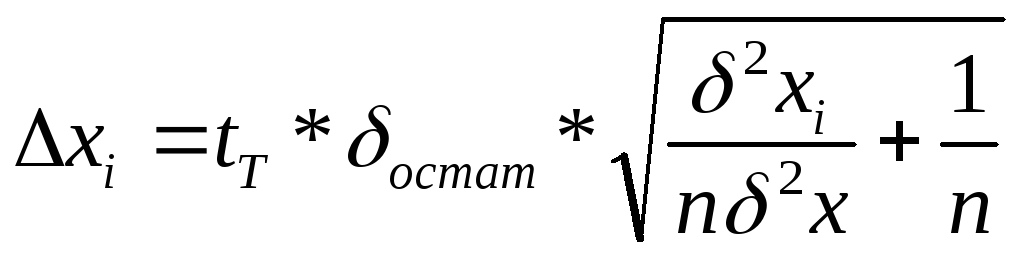m – число коэффициентов

;

математическое ожидание

Анализ этих формул показывает, что кривые доверительного интервала отходят от кривой регрессии с увеличением Х :