Корреляционно-регрессионный анализ

В научной инженерной практике достаточно часто приходится заниматься методами оценивания различных наблюдений. Для реализации процедуры оценивания предполагается, что заданы некоторые совокупности данных об измеряемых параметрах сложных систем. Эти совокупности данных называются выборками (имеющиеся данные отражают не все множество таких данных, а лишь некоторую выбранную случайным образом совокупности или выборку данных). Большинство этих данных в силу случайности своего характера имеют некоторое распределение плотности вероятности, которое влияет на применяемые методы оценки. Необходимо учитывать, что любые измерения содержат ошибки. По характеру их разделяют на систематические и случайные.

Систематические порождаются определенными закономерностями, существующими при данных условиях эксперимента, либо объективными факторами присущих исследуемому объекту. Случайные ошибки при данных условиях эксперимента характеризуются непостоянностью, т.к. отражают воздействие многих, но не определяющих факторов. Основной задачей математической статистики при обработке совокупности данных является определение численных параметров или функций, характеризующих вероятностные свойства рассматриваемых данных. Примерами таких свойств являются: математическое ожидание выборки, разброс выборки относительно математического ожидания, корреляционный коэффициент, определяющий связь данных между собой, функция распределения или спектральная плотность.

Такое определение интересующих нас величин практически невозможно, т.к. полученные из опыта результаты являются случайными, поэтому получаются приближенные оценки, важными свойствами которых являются:

1. Состоятельность, т.е. при возрастании объема выборки вероятность сколь угодно малых отклонений от оцениваемой величины стремится к 0.

2. Несмещенность – математическое ожидание равно оцениваемой величине. Требование несмещенной оценки к требованию отсутствия систем ошибки. Оценки, несмещенные и обладающие наименьшей возможной дисперсией называются эффективными.

Кроме этих характеристик используется также понятие точности полученной оценки. Для этого используется понятие доверительного интервала и доверительной вероятности.

Если а – оцениваемый параметр, а` - его оценка, мы не хотим, чтобы а` была больше (меньше) a`+/- ε, то вероятность такого события записывается так:

P(a- ε < a` < a+ ε) = α – доверительная вероятность

(a-ε;a+ ε) – доверительный интервал

Вычисление вероятности зависит от закона распределения её плотности. Для оценки её вида используются гистограммы. Ось значений случайных величин разбивают на интервалы. Для расчета длины (l) интервала можно использовать формулу:

, где n – число наблюдений

Каждому интервалу указывается интервал значений величины Х. Подчитывая число элементов Х, попавших в тот или иной интервал, можно построить гистограмму.

Ступенчатый график гистограммы обычно сглаживают непрерывной гладкой функцией (для этого можно использовать метод наименьших квадратов). Вид этой функции проверяют на соответствие известным законом распределения плотности вероятности. Обычно принимается, что случайная величина распределена по нормальному закону. Выбор закона определен следующими обстоятельствами:

1. Закон зависит только от 2 параметров (средних значений и дисперсии).

2. Нормальная плотность довольно точно отражает широкий круг случайных явлений природы.

3. Нормальная плотность связана с центральной предельной теоремой, которая утверждает, что распределение выборочных (средних) значений, случайно отобранных из генеральной совокупности т.е. теоретически полной) с известной конечной дисперсией асимптотически приближается по мере увеличения объема выборки к нормальному распределению.

Для одной случайной величины Х этот закон плотности имеет вид:

– математическое ожидание

σ² – дисперсия – характеристика разброса величины Х от своего математического ожидания.

Одинаковые дисперсии но разные мат ожидания

Одинаковые мат ожидания, но разные дисперсии

Дисперсия дает меру рассеяния плотности вероятности. Кривые нормальной плотности стремятся к нулю, но нигде его не достигают. При разных сигма и Мат ожидании получаются разные нормальные плотности с которыми неудобно работать, т.к. каждый раз надо вычислять значения по сложным формулам, поэтому целесообразно провести нормировку в виде:

, тогда

Z=0

=0

Для такого распределения составим специальные таблицы:

Свойства математического ожидания.

1.

2.

3.

Свойства дисперсии.

1.

2.

3.

не смещённые и состоятельные

даёт несмещённую оценку

асимптотически эффективная оценка

,

т.е. средняя арифметическая величина в раз точнее отдельного измерения.

Если использовать доверительные вероятность и интервал , то

, где - функция, обратная функции Лапласа

Если , то можно воспользоваться специальными таблицами для

Доверительная оценка для математического ожидания измеряемой величины x будет иметь вид:

Здесь характеризует уровень вероятности, с которой необходимо получить оценку

Пусть имеется некоторая выборка, содержащая измерения (m+1) переменных .(y, x_{1, …,} x_m ), т.е. рассматривается (m+1)-мерное пространство. Каждая точка этого пространства есть значение (m+1) переменных. Ставится задача выявить степень зависимости переменной y от остальных переменных x_{1, …,} x_m. Возможны два случая:

1. все переменные x_i не зависят друг от друга

2. часть переменных x_i зависит друг от друга, что вносит искажения в зависимость y(x_i).

Для случая (1) задача ясна и можно установить зависимость y=f(x_{1, …,} x_m) каким-нибудь способом (МНК, например). n≥m

Для случая (2) надо выявить зависимые друг от друга переменные x_i . Для этого определяются частные коэффициенты корреляции (т.е. коэф-ты, устанавливающие степень зависимости x_i от x_j ) по формулам:

, где

Если определить все частные коэффициенты корреляции, то можно построить ковариационную матрицу ( матрицу связей) К.

Если , то между х_i и х_j нет связи.

Если , то имеется строгая функциональная зависимость, однако аналитически вид этой зависимости нам не известен, её можно попытаться определить МНК (например), задавая различные функции их взаимосвязи. Считается, что если , то связь между этими переменными достаточно тесная.

Если значение коэффициента корреляции достаточно мало, то можно считать, что переменные независимы.

Если , то для удаления связи вычеркивается i (j) строка и столбец в матрице К, (тогда y= f(x₁…x_m) приближается к функции правильно описывающей работу системы)

Из сказанного очевидно, что для случая (1) получим диагональную матрицу.

С помощью матрицы К можно выразить совместную плотность вероятности переменных х_i.

Для двумерного случая:

Графически совместную плотность вероятности можно представить так:

Х1

После анализа матрицы К можно попытаться установить связь между У и Xi(i=1,m). Можно считать, что некоторая связь имеется, но мы не знаем её аналитической зависимости. Предположим, что эта связь имеет линейный характер.

Y = α0+ α1*x1+ αm*xm – уравнение регрессии.

У – предполагаемая зависимость.

Если потребовать, чтобы , то частные производные равны 0.

{m+1 уравнение

Решая полученную систему уравнений относительно , получим значения неизвестных в уравнении регрессии.

Эту задачу можно решить и в матричной форме.

Чтобы узнать, на сколько точно угадана зависимость в виде уравнение регрессии необходимо определить коэффициент корреляции этой регрессии.

, где

Будем считать, что коэффициент в уравнении регрессии определены. Сделаем замену переменных.

i – номер переменной, j – номер опыта

В силу свойств математического ожидания и дисперсии.

Имеем:

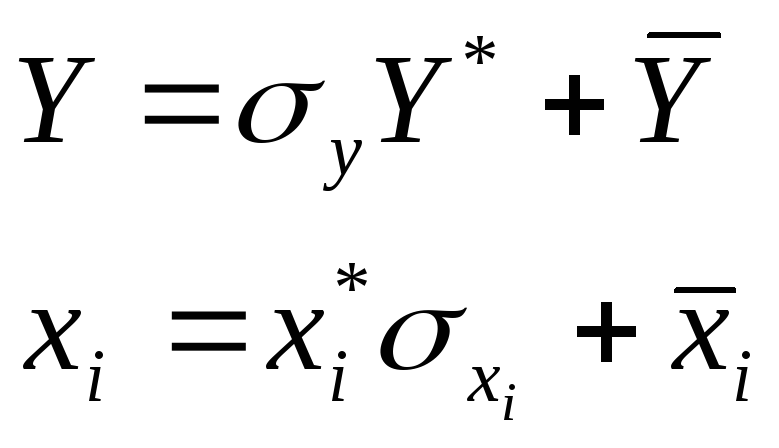
Подставляем эти выражения в уравнение регрессии, получим:

т.к. математические ожидания левой и правой частей уравнения регрессии равны.

Окончательно получаем:

В этом уравнении направление эффекта, вызванным изменением , определяется знаком , а величина эффекта от пропорциональна абсолютному значению коэффициента .