
- •Министерство образования республики беларусь
- •Тема 1. Логика и множества (основные понятия)
- •2. Укажите верное определение.
- •3. Укажите верное определение.
- •4. Укажите верное определение.
- •5. Укажите верное определение.
- •6. Укажите верное определение.
- •7. Укажите верное определение.
- •8. Укажите верное определение.
- •9. Укажите верное определение.
- •10. Укажите верное определение.
- •Тема 2. Матрицы, определители, числа, векторные пространства (основные понятия)
- •Тема 3. Основные факты
- •Тема 4. Логика. Множества. Основные алгебраические структуры
- •Тема 5. Системы линейных уравнений и арифметические векторы
- •Тема 6. Матрицы и определители
- •Тема 7. Теория чисел
- •Тема 8. Векторные и евклидовы пространства, линейные операторы
Тема 8. Векторные и евклидовы пространства, линейные операторы
1. Подпространством
арифметического векторного пространства
R![]() является множество всех векторов, сумма
координат которых равна:
является множество всех векторов, сумма
координат которых равна:
А) –1; В) 0;
Б) 1; Г) 2.
2. Пусть V — множество всех направленных отрезков, отложенных от начала координат. Укажите истинные утверждения.
А) Линейная оболочка всякого ненулевого вектора первого координатного угла есть все векторы этого угла, включая векторы на осях.
Б) Линейная оболочка двух различных ненулевых векторов из первого координатного угла есть множество всех векторов первого и третьего координатных углов.
В) Линейная оболочка всякого ненулевого вектора из первого координатного угла есть все векторы верхней полуплоскости.
Г) Линейная оболочка ненулевого вектора есть множество всех векторов прямой, проходящей через начало координат и имеющей направляющим вектором данный вектор.
3. Система векторов векторного пространства является его базисом, если:
А) ее линейная оболочка совпадает со всем пространством.
Б) данная система линейно независимая и ее линейная оболочка совпадает со всем пространством;
В) данная система линейно независима;
Г) всякий вектор пространства хотя бы одним образом выражается через эту систему.
4. Для любых
подпространств L![]() и
L
и
L![]() векторного
пространства V
истинно равенство:
векторного
пространства V
истинно равенство:
А)
dim (L![]() ∩ L
∩ L![]() )
= dim L
)
= dim L![]() + dim L
+ dim L![]() ;
;
Б)
dim (L![]() ∩ L
∩ L![]() )
= dim L
)
= dim L![]() + dim L
+ dim L![]() + dim (L
+ dim (L![]() + L
+ L![]() );
);
В)
dim (L![]() ∩ L
∩ L![]() )
= dim L
)
= dim L![]() + dim L
+ dim L![]() – dim (L
– dim (L![]() + L
+ L![]() );
);
Г)
dim (L![]() ∩ L
∩ L![]() )
= dim (L
)
= dim (L![]() + L
+ L![]() )
– (dim L
)
– (dim L![]() + dim L
+ dim L![]() ).
).
5. В пятимерном векторном пространстве два подпространства размерностей 2 и 3 имеют пересечение размерности m. Верно, что:
А) в любом случае m ≠ 0;
Б) в любом случае m = 1;
В) в любом случае m = 2;
Г)
(m
= 0)
![]() (m
= 1)
(m
= 1)
![]() (m
= 2).
(m
= 2).
6. Пусть а(![]() ),
b(
),
b(![]() )
— произвольные векторы арифметического
векторного пространства R
)
— произвольные векторы арифметического
векторного пространства R![]() ,
заданные своими координатами в некотором
базисе. Это пространство будет евклидовым,
если скалярное произведение определено
следующим образом:
,
заданные своими координатами в некотором
базисе. Это пространство будет евклидовым,
если скалярное произведение определено
следующим образом:
А) ab
=
![]() ;
;
Б) ab
=
![]() ;
;
В) ab
=
![]() ;
;
Г)
ab
=
![]() .
.
7. Пусть а(![]() ),
b(
),
b(![]() )
— произвольные векторы арифметического
векторного пространства R
)
— произвольные векторы арифметического
векторного пространства R![]() ,
заданные своими координатами в некотором
базисе. Это пространство будет евклидовым,
если скалярное произведение определено
следующим образом:
,
заданные своими координатами в некотором
базисе. Это пространство будет евклидовым,
если скалярное произведение определено
следующим образом:
А) ab
=
![]() ; В)
ab
=
; В)
ab
=
![]() ;
;
Б)
ab
=
![]() ; Г)
ab
=
; Г)
ab
=
![]() .
.
8. В двумерном
векторном пространстве с базисом e(![]() отображение f
вектору a(
отображение f
вектору a(![]() )
ставит в соответствие вектор b.
Отображение f
является линейным оператором, если
координаты вектора b
равны:
)
ставит в соответствие вектор b.
Отображение f
является линейным оператором, если
координаты вектора b
равны:
А)
(2a![]() ;
3a
;
3a![]() ); В)
(a
); В)
(a![]() +2;
a
+2;
a![]() );
);
Б)
(a![]() ;
a
;
a![]() +3); Г)
(a
+3); Г)
(a![]() +2;
3a
+2;
3a![]() ).
).
9. Множество M матриц с операциями сложения матриц и умножения матрицы на действительное число образует векторное пространство, если:
А) M
=
![]() ; В)
M
=
; В)
M
=
![]() ;
;
Б)
M
=![]() ; Г)
M
=
; Г)
M
=
![]() .
.
10. Следующее множество матриц с операциями сложения и умножения матриц на элемент из R образует векторное пространство:
А)
![]() ; В)
; В)
![]() ;
;
Б)
![]() ; Г)
; Г)
![]() .
.
11. Следующее множество матриц с операциями сложения и умножения матриц на элемент из R образует векторное пространство:
А)
![]() ; В)
; В)
![]() ;
;
Б)
![]() ; Г)
; Г)
![]() .
.
12. Следующее множество матриц с операциями сложения и умножения матриц на элемент из R образует векторное пространство:
А)
![]() ; В)
; В)
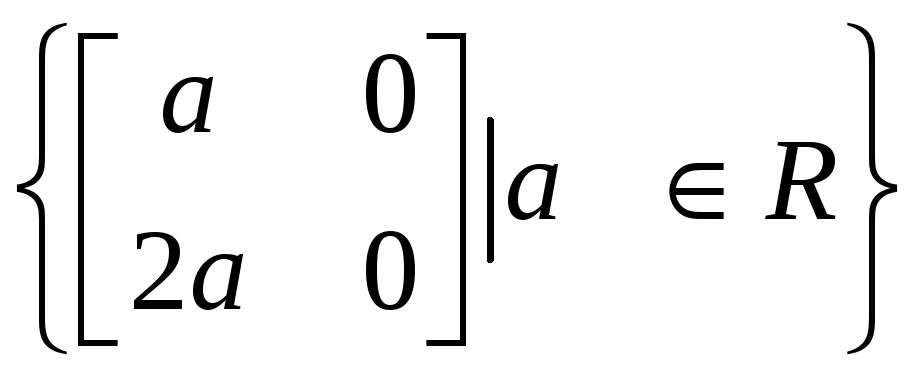 ;
;
Б)
![]() ; Г)
; Г)
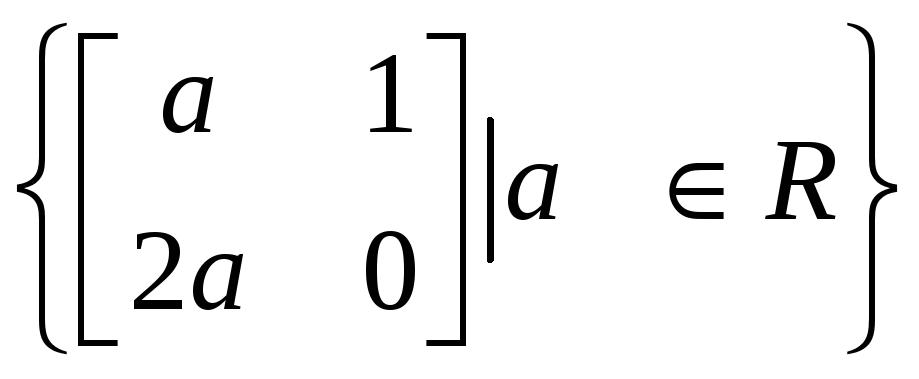 .
.
13. Следующее множество матриц с операциями сложения и умножения матриц на элемент из R образует векторное пространство:
А)
![]() ; В)
; В)
![]() ;
;
Б)
![]() ; Г)
; Г)
![]() .
.
14. Векторы а1(m; 1; 0), a2(2; m; 1), a3(1; 0; 1) в пространстве R3 линейно зависимы, если:
A) m = ±2; В) m = 0;
Б) m = ± 3; Г) m = ± 1.
15. Векторы а1(m; 2; 0), a2(1; 1; 0), a3(–1; 1; m) в пространстве R3 линейно зависимы, если:
A) m = 0 или m = 2; В) m = ±2;
Б) m = 1; Г) m = –1.
16. Векторы а1(1; 0; m), a2(2; m; 1), a3(m; 0; 1) в пространстве R3 линейно зависимы, если:
A) m = ±2; В) m = 2 или m = ±1;
Б) m = 0 или m = ±1; Г) m = 0.
17. Векторы а1(2; 1; k), a2(1; 0; k), a3(–1; 0; 2) в пространстве R3 линейно зависимы, если:
A) k = 1; В) k = –2;
Б) k = –1; Г) k = 2.
18. Векторы а1(–1; 2k; 3), a2(0; 3k; –k), a3(1; k; –4) в пространстве R3 линейно зависимы, если:
A) k = ±1; В) k = ±3;
Б) k = 0 или k = 1; Г) k = 1 или k = 3.
19. Вектор b(–1; 4; 5) пространства R3 в базисе, состоящем из векторов а1(1; 0; 1),
a2(–2; 1; 0), a3(0; –1; 2) имеет координаты:
A) (1; 1; –3); В) (–3; 1; 0);
Б) (–1; –1; 1); Г) (–1; 0; 1).
20. Вектор b(4; –1; 3) пространства R3 в базисе, состоящем из векторов а1(1; 0; 1), a2(0; 2; 1), a3(–2; 3; 0) имеет координаты:
A) (0; 1; –2); В) (2; 1; –1);
Б) (4; 0; 0); Г) (6; –1; 1).
21. Вектор c(2; –1; 2) пространства R3 в базисе, состоящем из векторов а1(1; 2; 0), a2(0; 1; 3), a3(3; 0; –1) имеет координаты:
A) (2; 0; 1); В) (–1; 0; 1);
Б) (–1; 1; 1); Г) (–2; 1; 1).
22. Вектор c(–2; 5; 8) пространства R3 в базисе, состоящем из векторов а1(–2; 3; 4), a2(1; 0; 1), a3(2; –1; 0) имеет координаты:
A) (1; 0; 2); В) (0; –2; 1);
Б) (1; –1; 0); Г) (2; 0; 1).
23. Вектор d(1; 4; 4) пространства R3 в базисе, состоящем из векторов а1(1; –1; 1), a2(0; 2; 1), a3(1; 0; 3) имеет координаты:
A) (1; 3; 0); В) (2; 0; –1);
Б) (0; 1; 1); Г) (0; 2; 1).
24. Размерность линейной оболочки системы векторов а1(1; 1; 1; 2), a2(2; 0; 1; 1), a3(0; 2; 1; 3), a4(1; –1; 0; –1) равна:
A) 4; В) 2;
Б) 3; Г) 1.
25. Размерность линейной оболочки системы векторов а1(1; 3; 0; –1), a2(0; –1; 1; 1), a3(1; 2; 1; 1), a4(1; 4; –1; –2) равна:
A) 1; В) 2;
Б) 3; Г) 4.
26. Размерность линейной оболочки системы векторов b1(–1; 1; 1; 1), b2(1; 1; –1; 1), b3(0; 2; 0; 2), b4(–2; 0; 2; 0) равна:
A) 2; В) 3;
Б) 1; Г) 4.
27. Размерность линейной оболочки системы векторов b1(2; 0; –1; 2), b2(1; 1; –1; 1), b3(1; –1; 0; 1), b4(0; 2; –1; 0) равна:
A) 1; В) 3;
Б) 2; Г) 4.
28. Размерность линейной оболочки системы векторов c1(1; 0; 1; –1), c2(0; 2; 0; 1), c3(–1; 2; –1; 1), c4(1; –1; 0; –1) равна:
A) 1; В) 3;
Б) 2; Г) 4.
29. В пространстве многочленов степени не выше 3 система многочленов x – 1, x, x2 – 2, 2x3 образует базис. Координаты многочлена f(x) = –1 + 4x – x2 + 4x3 в этом базисе:
A) (1; 2; –6; 4); В) (1; 2; 2; 2);
Б) (3; 1; –1; 2); Г) (–1; 2; 6; 4).
30. В пространстве многочленов степени не выше 3 система многочленов 1 – x, x, x2, x3 – x образует базис. Координаты многочлена f(x) = 2 – 3x – x2 + 3x3 в этом базисе:
A) (2; 2; –1; 3); В) (1; –1; 1; –1);
Б) (2; –3; –1; 3); Г) (2; –1; 0; 3).
31. В пространстве многочленов степени не выше 3 система многочленов x2+1, x–1, x3, x3–x2 образует базис. Координаты многочлена f(x) = 1 + x – x2 + 2x3 в этом базисе:
A) (1; 1; –1; 2); В) (2; 1; –1; 3);
Б) (1; –1; 2; 3); Г) (–2; 1; 1; –3).
32. В пространстве многочленов степени не выше 3 система многочленов 3 – x, x2 + 2, x2 –x, x3 + 1 образует базис. Координаты многочлена f(x) = –3x + x2 – x3 в этом базисе:
A) (1; –1; 1; –1); В) (0; –3; 1; 1);
Б) (–3; 1; –1; 0); Г) (1; –1; 2; –1).
33. В пространстве многочленов степени не выше 3 система многочленов 2 – x, x2 + x, 2x3 – x, x3 + x2 образует базис. Координаты многочлена f(x) = 4 – 3x – 3x2 – x3 в этом базисе:
A) (4; –3; –3; –1); В) (2; 1; 0; –3);
Б) (2; 0; 1; –3); Г) (0; –3; –3; 2).
34. Найдите размерность суммы и размерность пересечения подпространств L1 = L(a1; a2; a3), L2 = L(b1; b2), если а1(1; 2; 0; 1), a2(1; 1; 1; 0), a3(0; 1; –1; 1), b1(1; 0; 1; 0), b2(1; 3; 0; 1):
A) dim(L1 + L2) = 4, dim(L1 ∩ L2) = 1;
Б) dim(L1 + L2) = 5, dim(L1 ∩ L2) = 0;
В) dim(L1 + L2) = 3, dim(L1 ∩ L2) = 2;
Г) dim(L1 + L2) = 3, dim(L1 ∩ L2) = 1.
35. Найти размерность суммы и размерность пересечения подпространств L1 = L(a1; a2; a3), L2 = L(b1; b2), если а1(1; 1; 1; 1), a2(1; 0; 3; –1), a3(1; 2; –1; 3), b1(1; 2; 0; 2), b2(1; 0; –1; 0):
A) dim(L1 + L2) = 4, dim(L1 ∩ L2) = 0;
Б) dim(L1 + L2) = 5, dim(L1 ∩ L2) = 0;
В) dim(L1 + L2) = 3, dim(L1 ∩ L2) = 1;
Г) dim(L1 + L2) = 4, dim(L1 ∩ L2) = 1.
36. Найти размерность суммы и размерность пересечения подпространств L1 = L(a1; a2; a3), L2 = L(b1; b2), если а1(1; 1; –1; 1), a2(1; –1; 1; –1), a3(3; 1; –1; 1), b1(0; –1; 1; –1), b2(1; 0; –1; 1):
A) dim(L1 +L2) = 3, dim(L1 ∩ L2) = 1;
Б) dim(L1 + L2) = 4, dim(L1 ∩ L2) = 1;
В) dim(L1 + L2) = 3, dim(L1 ∩ L2) = 2;
Г) dim(L1 + L2) = 2, dim(L1 ∩ L2) = 2.
37. Найти размерность суммы и размерность пересечение подпространств L1 = L(a1; a2), L2 = L(b1; b2; b3), если а1(1; 1; –2; 1), a2(2; 0; 1; –1), b1(0; 2; –3; 3), b2(3; 1; –1; 0), b3(1; –1; 3; –2):
A) dim(L1 +L2) = 3, dim(L1 ∩ L2) = 1;
Б) dim(L1 + L2) = 4, dim(L1 ∩ L2) = 0;
В) dim(L1 + L2) = 2, dim(L1 ∩ L2) = 2;
Г) dim(L1 + L2) = 3, dim(L1 ∩ L2) = 2.
38. Найти размерность суммы и размерность пересечение подпространств L1 = L(a1; a2), L2 = L(b1; b2; b3), если а1(3; –1; 0; 1), a2(–1; 0; 1; 2), b1(2; –1; 1; 3), b2(4; –1; –1; –1), b3(1; 1; –1; 0):
A) dim(L1 +L2) = 4, dim(L1 ∩ L2) = 1;
Б) dim(L1 + L2) = 3, dim(L1 ∩ L2) = 1;
В) dim(L1 + L2) = 3, dim(L1 ∩ L2) = 2;
Г) dim(L1 + L2) = 2, dim(L1 ∩ L2) = 2.
39. Укажите преобразование φ трехмерного пространства, являющееся линейным оператором:
A) φ(x1; x2; x3) = (x1 – x2, x1 + x2, x3 + 2);
Б) φ(x1; x2; x3) = (x12, x2, 2x3);
В) φ(x1; x2; x3) = (x1 – x2, x1 + x2, 3x3);
Г) φ(x1; x2; x3) = (x1, x2 + 1, x3 + 2).
40. Укажите преобразование φ трехмерного пространства, являющееся линейным оператором:
A) φ(x1; x2; x3) = (0, x2, x32);
Б) φ(x1; x2; x3) = (x1, 2x2, 3x3);
В) φ(x1; x2; x3) = (2x1, x2 – x1, x3 – x12);
Г) φ(x1; x2; x3) = (x1 + x2 + x3, x2, x33).
41. Укажите преобразование φ трехмерного пространства, являющееся линейным оператором:
A) φ(x1; x2; x3) = (x1 – x2 + x3, x2, x3);
Б) φ(x1; x2; x3) = (2x1 + x2, 0, x3 + 1);
В) φ(x1; x2; x3) = (x1 + 1, 0, x3 + x2);
Г) φ(x1; x2; x3) = (x1; x22, 3x3).
42. Укажите преобразование φ трехмерного пространства, являющееся линейным оператором:
A) φ(x1; x2; x3) = (x1; x2 + x3; x3 + x2 + 1);
Б) φ(x1; x2; x3) = (x1; x2 + 2, 2x3);
В) φ(x1; x2; x3) = (x1 – x2, x2 + x3, 2x3);
Г) φ(x1; x2; x3) = (2x1; x23, x1 + x2 + x3).
43. Укажите преобразование φ трехмерного пространства, являющееся линейным оператором:
A) φ(x1; x2; x3) = (x12; 2x2; 0);
Б) φ(x1; x2; x3) = (x1 + x2 + x3; 0, x12 + x3);
В) φ(x1; x2; x3) = (x1 + x2, x22, 0);
Г) φ(x1; x2; x3) = (x1 + x2 + x3, 0; x2 – x3).
44. Пусть a = e1 + 2e2 + e3 + 2e4 и b = 3e1 + e2 – e3 + 2e4, базис e ортонормированный. Скалярное произведение ab равно:
A) 8; В) 0;
Б) 6; Г) –8.
45. Пусть a = –e1 + 2e2 + e3 – e4 и b = –2e1 + e2 + 3e3 + e4, базис e ортонормированный. Скалярное произведение ab равно:
A) 1; В) 6;
Б) 5; Г) –1.
46. Пусть a = e1 + e2 – 3e4 и b = e1 – 5e2 + 7e3 – 2e4, базис e ортонормированный. Скалярное произведение ab равно:
A) 17; В) 10;
Б) 2; Г) –10.
47. В евклидовом пространстве R4 угол между векторами а(1; 2; 1; –1), b(–2; 1; 1; 1) равен:
A) π; В) π/2;
Б) π/3; Г) π/4.
48. В евклидовом пространстве R4 угол между векторами а(1; 1; 1; 1), b(1; 1; 3; –5) равен:
A) π/4; В) π/6;
Б) π; Г) π/2.
49. В двумерном евклидовом пространстве дан базис e = (e1, e2) и линейный оператор φ поворота на угол π/4 против часовой стрелки. Матрица А линейного оператора φ в базисе e имеет вид:
A)![]() ; В)
; В)
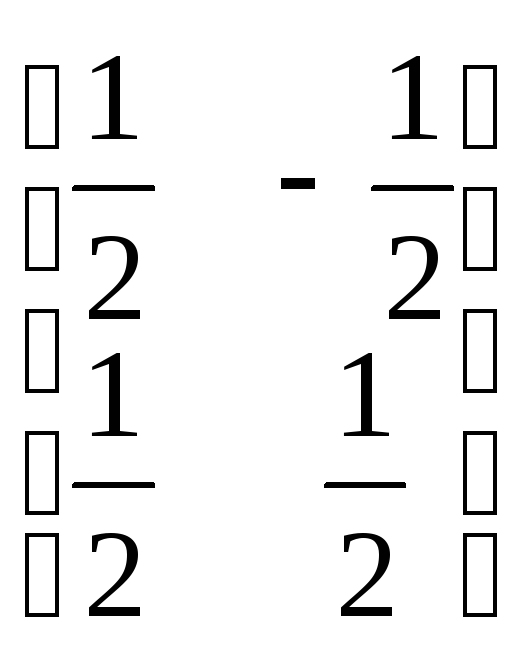 ;
;
Б)
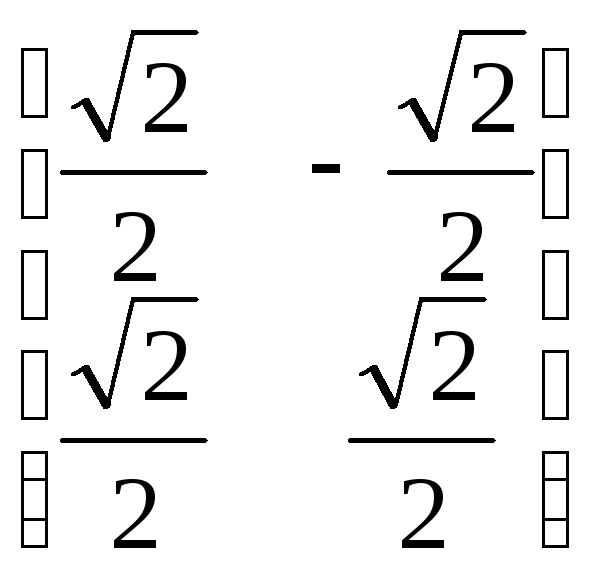 ; Г)
; Г)
![]() .
.
50. В двумерном евклидовом пространстве дан базис e = (e1, e2) и линейный оператор φ поворота на угол 2π/3 против часовой стрелки. Матрица А линейного оператора φ в базисе e имеет вид:
A)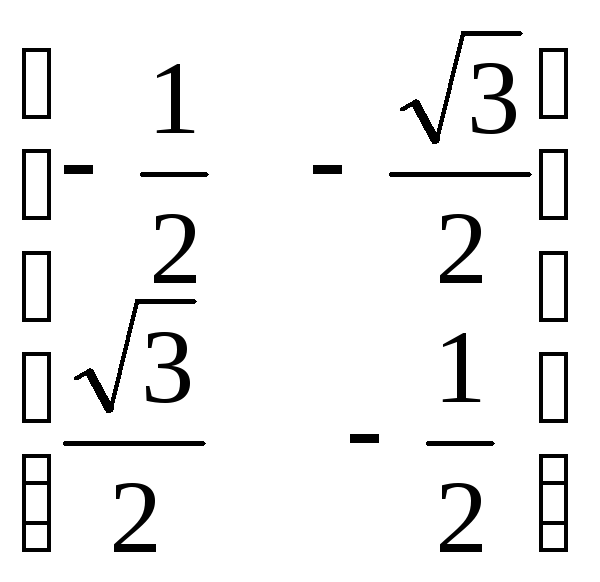 ; В)
; В)
![]() ;
;
Б)
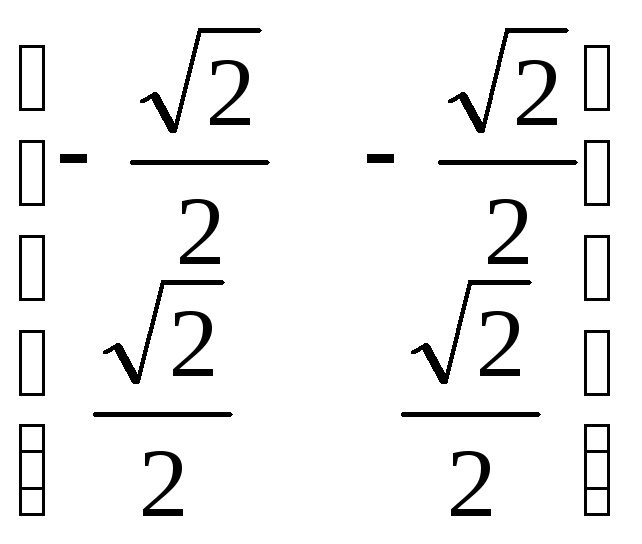 ; Г)
; Г)
![]() .
.
51. В двумерном евклидовом пространстве дан базис e = (e1, e2) и линейный оператор φ, который вектор e1 поворачивает на угол π/2 по часовой стрелке, а вектор e2 растягивает вдвое. Матрица А линейного оператора φ в базисе e имеет вид:
A)![]() ; В)
; В)
![]() ;
;
Б)
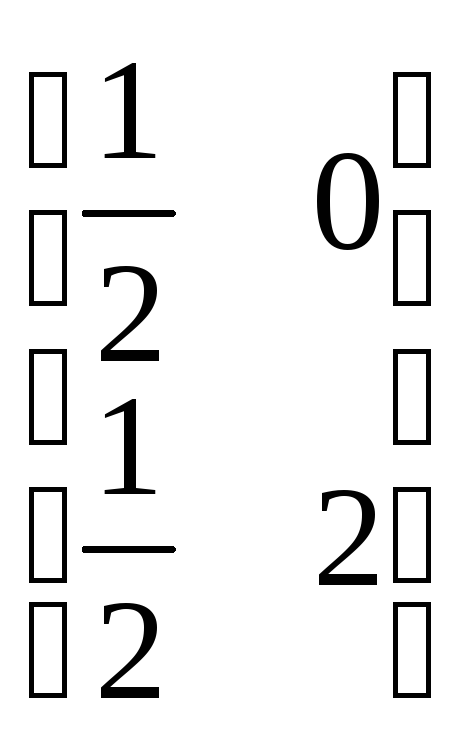 ; Г)
; Г)
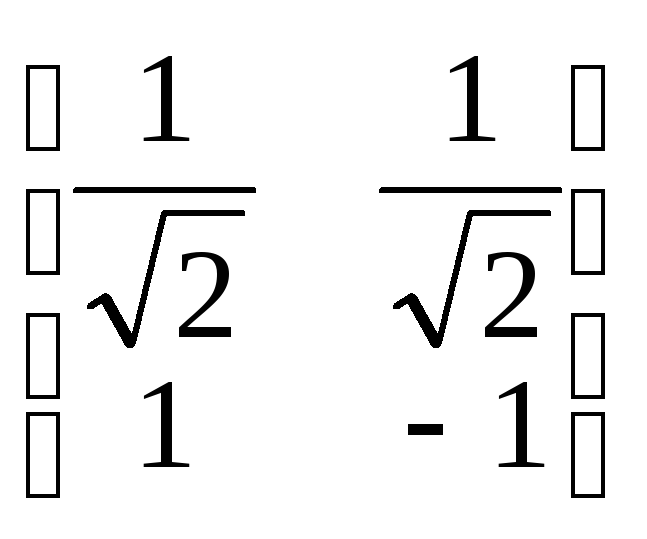 ,
,
52. В двумерном евклидовом пространстве дан базис e = (e1, e2) и линейный оператор φ, который вектор e1 поворачивает на угол π, а вектор e2 поворачивает на угол π/3 по часовой стрелке. Матрица А линейного оператора φ в базисе e имеет вид:
A)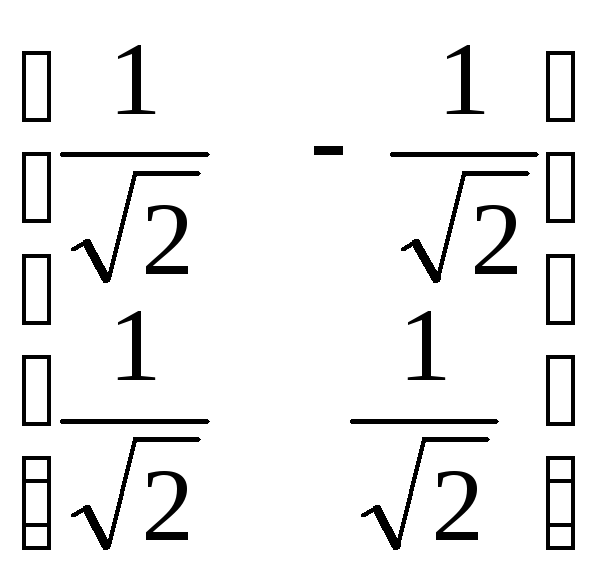 ; В)
; В)
![]() ;
;
Б)
![]() ; Г)
; Г)
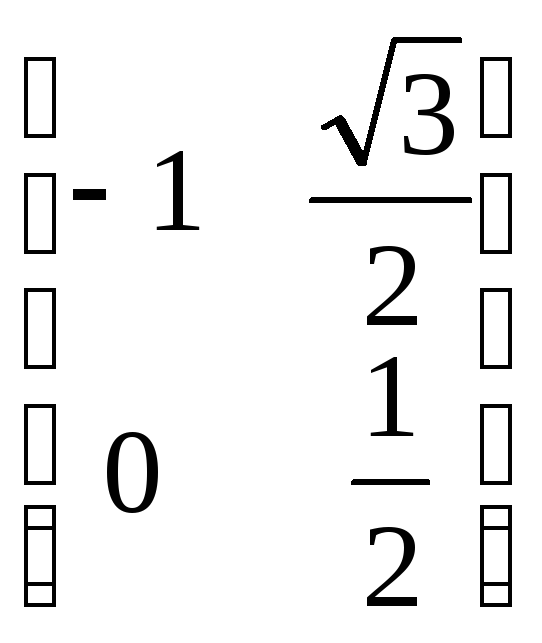 .
.
53. В двумерном евклидовом пространстве дан базис e = (e1, e2) и линейный оператор φ, который вектор e1 поворачивает на угол π, а вектор e2 поворачивает на угол π/6 против часовой стрелки. Матрица А линейного оператора φ в базисе e имеет вид:
A)![]() ; В)
; В)
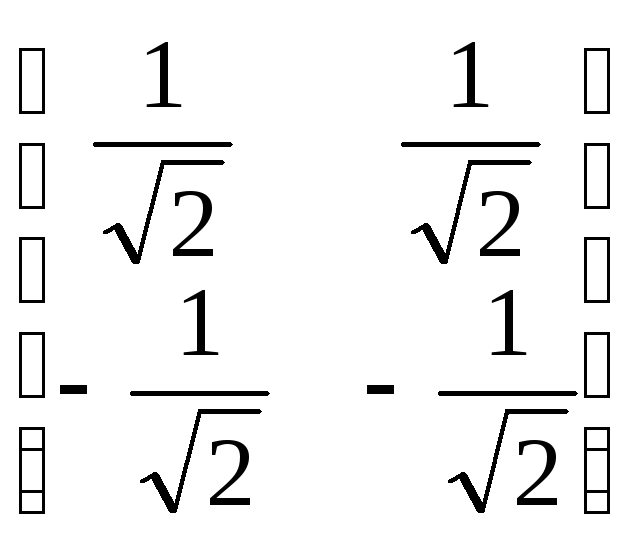 ;
;
Б)
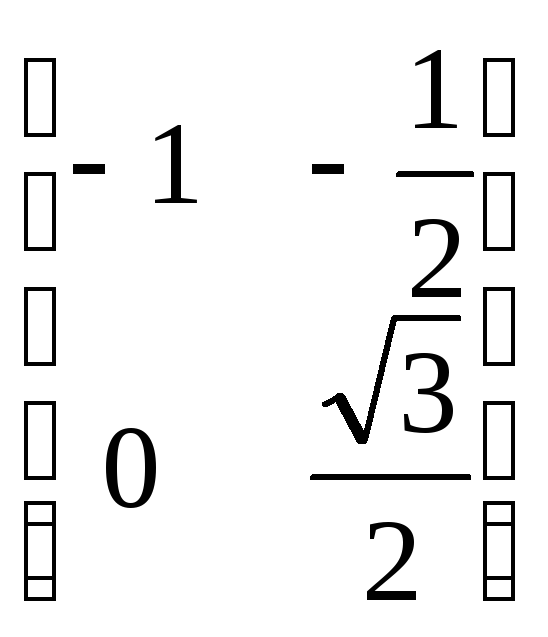 ; Г)
; Г)
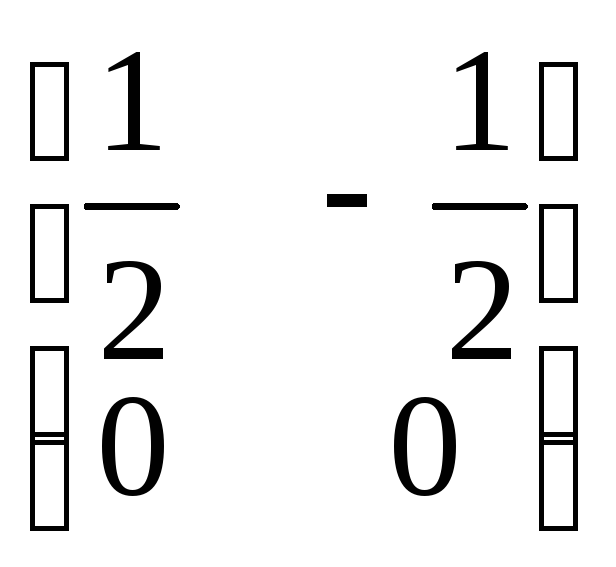 .
.
54. Если в пространстве
R2
линейный оператор φ в некотором базисе
задан матрицей
![]() ,
то собственные значения линейного
оператора равны:
,
то собственные значения линейного
оператора равны:
A) λ1 = λ2 = –1; В) λ1 = 2, λ2 = –1;
Б) λ1 = 1, λ2 = –1; Г) λ1 = 2, λ2 = 1.
55. Если в пространстве
R2
линейный оператор φ в некотором базисе
задан матрицей
![]() ,
то собственные значения линейного
оператора равны:
,
то собственные значения линейного
оператора равны:
A) λ1 = 1, λ2 = –1; В) λ1 = 2, λ2 = 5;
Б) λ1 = 0, λ2 = 5; Г) λ1 = λ2 = 5.
56. Если в пространстве
R2
линейный оператор φ в некотором базисе
задан матрицей
![]() ,
то собственные значения линейного
оператора равны:
,
то собственные значения линейного
оператора равны:
A) λ1 = λ2 = 1; В) λ1 = 3, λ2 = –3;
Б) λ1 = 0, λ2 = 3; Г) λ1 = 1, λ2 = –1.
57. Матрица
![]() приводится к диагональной матрице:
приводится к диагональной матрице:
A)![]() ; В)
; В)
![]() ;
;
Б)
![]() ; Г)
; Г)
![]() .
.
58. Матрица
![]() приводится к диагональной матрице:
приводится к диагональной матрице:
A)![]() ; В)
; В)
![]() ;
;
Б)
![]() ; Г)
; Г)
![]() .
.
ОТВЕТЫ
Тема 1
1А, 2Б, 3В, 4Г, 5В, 6В, 7Б, 8В, 9А, 10А, 11Г, 12Б, 13Б, 14В, 15В, 16Г, 17Б, 18А, 19Б, 20Г,
Тема 2
1Г, 2Г, 3В, 4Б, 5Г, 6Б, 7Б, 8Б, 9Б, 10Г, 11В, 12Г, 13В, 14В, 15Б, 16А, 17Б, 18Г, 19В, 20Г, 21В, 22А, 23Б, 24В, 25В, 26В, 27Г.
Тема 3
1В, 2А, 3А, 4В, 5В, 6Г, 7А, 8В, 9Б, 10Г, 11В, 12Б, 13В, 14Б, 15А, 16В, 17В, 18Б, 19Г, 20А, 21В, 22А, 23Б, 24В, 25Б, 26В, 27Б, 28В, 29Г, 30Г, 31А, 32А, 33В, 34В, 35Г, 36Б, 37Б, 38В, 39В, 40Г, 41В, 42В, 43Г, 44Б, 45Б, 46А.
Тема 4
1Г, 2А, 3В, 4В, 5Б, 6В, 7В, 8А, 9Б, 10Г, 11А, 12А, 13Г, 14Б, 15Г, 16Г, 17Б, 18В, 19В, 20Г, 21Б, 22А, 23Г, 24А, 25Б, 26В, 27В, 28Г, 29Б, 30А, 31Г, 32Б, 33Г, 34Б, 35Б, 36А, 37Г, 38Б, 39Б, 40В.
Тема 5
1Г, 2В, 3В, 4Б, 5Б, 6А, 7Г, 8В, 9В, 10Б, 11В, 12А, 13В, 14В, 15В, 16Г, 17В, 18А, 19Б, 20В, 21В, 22Б, 23Б, 24В, 25А, 26Б, 27В, 28Г, 29А, 30Б, 31А, 32А, 33В, 34В, 35А, 36В, 37Г, 38В, 39Б, 40Г, 41Г,
Тема 6
1А, 2В, 3Б, 4А, 5В, 6А, 7Б, 8Г, 9Б, 10Б, 11А, 12В, 13Г, 14А, 15Б, 16В, 17В, 18А, 19Б, 20Б, 21Г, 22Б, 23В, 24Г, 25В, 26В, 27А, 28В, 29Г, 30В, 31Б, 32В, 33А, 34Б, 35Г, 36Г, 37Г, 38Б, 39Г, 40В.
Тема 7
1Б, 2В, 3А, 4Б, 5Б, 6В, 7Г, 8В, 9В, 10А, 11Б, 12Г, 13Г, 14Б, 15Б, 16А, 17Г, 18Б, 19Б, 20Б, 21В, 22А, 23Г, 24Г, 25В, 26Г, 27Б, 28Г, 29В, 30Г, 31А, 32Г, 33А, 34Г, 35А, 36Г, 37А, 38Г, 39В, 40Г, 41Б, 42В, 43В, 44Б, 45Г, 46В, 47Б, 48В, 49А, 50Б.
Тема 8
1В, 2Г, 3Б, 4В, 5Г, 6Г, 7Б, 8А, 9Б, 10Г, 11А, 12В, 13Б, 14Г, 15А, 16Б, 17В, 18Б, 19А, 20В. 21Б, 22Г, 23А, 24В, 25Б, 26А, 27Б, 28Г, 29Б, 30А, 31В, 32Г, 33Б, 34Г, 35А, 36А, 37Г, 38В, 39В, 40Б, 41А, 42В, 43Г, 44А, 45В, 46Б, 47В, 48Г, 49Б, 50А, 51В, 52Г, 53Б, 54А, 55Б, 56В, 57А, 58Г.
