Часть II. Булевы функции
Таблицы значений булевых функций
2.1. Решить булевы уравнения:
а) x
y =
x
y; д)
~ y
= xy
;
б) x
| y
= 0; е)
y
= 1;
в)
x
y =
x
y;
ж) x
y
=
;
г)
x =
0; з) (y
(xz))
x
z
= (x
(y~z))
(xz
y)
2.2. Решить системы булевых уравнений:
а)
; б)
.
2.3. Построить таблицы значений для следующих булевых функций:
а) f(x,
y)
= (xy)
( xyx);
г) f(x,
y,
z)
= (x
)
| (xy
z);
б) f(x,
y)
= (x
(y
))
~ ((
x)x);
д) f(x,
y,
z)
= ((x|y)
)
(z
);
в) f(x,
y)
= (x
(
x))
(y
);
е) f(x,
y,
z)
= x (
|
z)
(yz)
.
2.4. Проверить, выполняются ли законы коммутативности и ассоциативности для сложения по модулю 2, стрелки Пирса и штриха Шеффера.
2.5. Булева функция n переменных принимает значение «1» на восьми наборах переменных. На скольких наборах переменных эта функция принимает значение «0», если
а) n = 3; б) n = 4; в) n = 5; г) n = 6?
2.6. Подсчитайте количество различных булевых функций n переменных, если
а) n = 1; б) n = 2; в) n = 3; г) n = 4.
Совершенные нормальные формы
2.7. Разложить булевы функции, представленные в таблице 1, в совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы.
Таблица 1.
|
x |
y |
z |
f1(x, y, z) |
f2(x, y, z) |
f3(x, y, z) |
f4(x, y, z) |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
1 |
2.8. Используя таблицы значений, разложить данные функции в совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы:
а) f(x, y) = x ~ y; д) f(x, y) = x y;
б) f(x, y) = x y; е) f(x, y) = (x y) ~ (x y);
в) f(x,
y)
= x
y;
ж) f(x,
y,
z)
= y ~
(x
y
);
г) f(x,
y)
= x |
y; (з)
f(x,
y,
z)
= (x
(
z))
(
|
z).
2.9. Используя таблицы значений, разложить данные функции в совершенную дизъюнктивную нормальную форму:
а) f(x) = 1; б) f(x, y) = 1; в) f(x, y, z) = 1.
2.10. Используя таблицы значений, разложить данные функции в совершенную конъюнктивную нормальную форму:
а) f(x) = 0; б) f(x, y) = 0; в) f(x, y, z) = 0.
Двойственная функция
2.11. Построив таблицы значений для заданных функций f, составить таблицы значений для двойственных функций f*. Восстановить вид f* с помощью наиболее экономичной совершенной нормальной формы.
а) f(x,
y)
= (x
~ (
x))
| (
0); в)
f(x,
y,
z)
= (
)
(xy~z);
б) f(x,
y,
z)
= (x|1)(y
(
x)); г)
f(x,
y,
z)
= (x|
)
(y(
y
x)).
2.12. С помощью таблиц значений выяснить, какие функции являются двойственными к следующим функциям:
а) эквивалентности, в) стрелке Пирса,
б) сложению по модулю 2, г) штриху Шеффера?
2.13. Используя принцип двойственности, найти функции f*, двойственные к данным функциям f.
а) f(x
,y,
z)
= (x
)
x
(
xy); в)
f(x,
y,
z)
= x
xy;
б) f(x,
y,
z)
=
(
x); г)
f(x,
y,
z)
= (x |
)
~ (y
(
x)).
Эквивалентные преобразования
2.14.
Найдите x,
если
b.
2.15. Упростить формулы:
а) x
(xy)
(x
);
д) (xz)
(((yz)xy)z);
б) xz
x
yz
yz;
е) (x
(
&x))
(y
);
в) (x~y)
(xy);
ж) ((xy)
)
| (z
);
г) (yx)
(yyx);
з) (x
(zy
x))
(x
)
y.
2.16. Используя эквивалентные преобразования, разложить данные функции в совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы:
а) f(x,
y)
= x (xy);
г) f(x,
y,
z)
= (
y)
;
б) f(x,
y)
= (xy)
(yx);
д) f(x,
y,
z)
= (
x)
~ (xy
);
в) f(x,
y,
z)
= (x
)
yz;
е) f(x,
y,
z)
= (x
(y
))
.
2.17. По таблицам значений (см. таблицу 1) найдите формулы, реализующие функции f1, f2, f3, f4, и придайте им более простой вид.
Релейно-контактные схемы (РКС)
2.18. Составить наиболее простые РКС для формул:
а) x
(
z
у)
; в)
(x
(z
))
~ ((
x)
z);
б) (xy)
(yz);
г) (z
(
x))
(y
).
2.19. Упростить РКС:
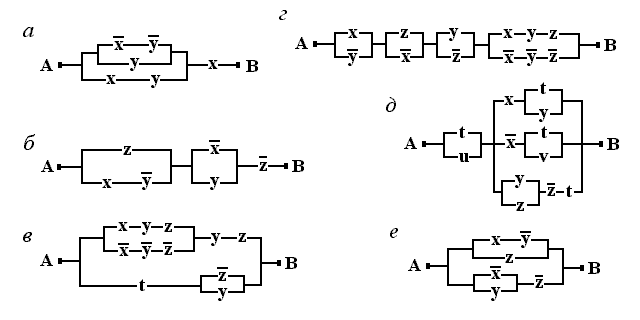
2.20. Построить наиболее простые РКС по заданным условиям работы:
а) f(0,0,1) = f(1,0,1) = f(1,1,1) = 1;
б) f(0,0,0) = f(0,1,0) = f(0,1,1) = f(1,1,1) = 1;
в) f(0,0,0,0) = f(0,0,1,1) = f(1,1,0,0) = 1;
г) f(0,1,0,1) = f(1,1,1,1) = 1,
а на остальных наборах значения функции f равны нулю.
2.21. Комитет состоит из пяти человек. Решение выносится большинством голосов. Если председатель голосует “против”, решение не принимается. Постройте такую схему, чтобы, голосуя “за”, каждый из пяти человек нажимал бы на кнопку, и в случае принятия решения зажигалась бы сигнальная лампочка.
2.22. Требуется, чтобы включение света в комнате осуществлялось с помощью трех различных переключателей таким образом, чтобы нажатие на любой из них приводило к включению света, если он перед этим был выключен, и к его выключению, если он был включен. Построить простую цепь, удовлетворяющую такому заданию.
Полином Жегалкина
2.23. Используя таблицы значений, разложить данные функции двух переменных в полином Жегалкина.
а) f(x,
y)
=
y;
в) f(x,
y)
= (y
)
| (xy);
б) f(x,
y)
= x
y;
г) f(x,
y)
= xy
.
2.24. Разложить в полином Жегалкина функции f1, f2, f3, f4, представленные в таблице 1.
2.25. Используя таблицы значений, разложить данные функции трёх переменных в полином Жегалкина.
а) f(x,
y,
z)
= x
(yz);
в) f(x,
y,
z)
=
;
б) f(x,
y,
z)
= (xz
y)
(xy
z); г)
f(x,
y,
z)
= (x
)
(
| z).
2.26. Путём эквивалентных преобразований преобразовать данные формулы в полином Жегалкина.
а)
; в)
(
~ y)
(xz
);
б)
xy; г)
(zy)
((y
)
xy
).
Функционально замкнутые классы
2.27. Какие из булевых функций f1, f2, f3, f4, представленных в таблице 1, принадлежат:
а) классу Т0 функций, сохраняющих константу 0;
б) классу Т1 функций, сохраняющих константу 1;
в) обоим классам и Т0, и Т1?
2.28. Среди булевых функций от одной и двух переменных найти все функции, сохраняющие 1, и все функции, сохраняющие 0.
2.29. Подсчитайте количество булевых функций от n переменных, сохраняющих константу 0, если n = 4.
2.30. Найти число булевых функций от n переменных, принадлежащих одновременно классам Т0 и Т1.
2.31. Какие из булевых функций f1, f2, f3, f4, представленных в таблице 1, являются самодвойственными?
2.32. Показать, что функция f(x, y, z) = xy yz zx является самодвойственной.
2.33. Булева функция четырёх переменных самодвойственна. На скольких наборах переменных она принимает значение “1”?
2.34. Подсчитайте количество самодвойственных булевых функций от n переменных, если n = 4.
2.35. Какие из булевых функций f1, f2, f3, f4, представленных в таблице 1, являются монотонными?
2.36. Построить все монотонные функции от двух переменных.
2.37. Какие из функций монотонны?
а) f(x,
y,
z)
= xy
xz 
;
б)
f(x,
y,
z)
= (
z)
z(xy);
в) f(x,
y,
z)
=
~
.
2.38. Среди булевых функций от одной и двух переменных найти все линейные функции.
2.39. Подсчитайте количество линейных булевых функций от n переменных, если n = 9.
2.40. К каким классам принадлежат данные булевы функции?
а) f(x,
y)
= x
y;
в) f(x,
y,
z)
= z
(xy)
xy
;
б) f(x,
y)
= x |
y;
г) f(x,
y,
z)
=
(z~y)
x
(yz
).
2.41. Доказать, что пересечение двух функционально замкнутых классов есть функционально замкнутый класс.
2.42. Доказать, что класс функций, сохраняющих константу 0, но не сохраняющих константу 1, не является функционально замкнутым.
2.43. Доказать, что объединение функционально замкнутых классов может не быть функционально замкнутым.
2.44. Доказать, что совокупность функций, двойственных функциям из функционально замкнутого класса, образует функционально замкнутый класс.
Полные системы
2.45. Преобразовать данные формулы таким образом, чтобы в их записи остались только: 1) отрицание и конъюнкция; 2) отрицание и дизъюнкция; 3) штрих Шеффера; 4) стрелка Пирса.
а) x
~ y;
в) xy
;
д) (xy)
;
б) x
y;
г)
yz;
е) x
z.
2.46. Используя теорему о функциональной полноте, проверить, являются ли полными следующие системы функций:
а) {
,
x1x2};
в) {x1x2,
x1x2,
1}; д) {0, x1x2}.
б) {
,
1}; г) {x1x2,
x1x2,
x1x2};
2.47. Используя теорему о функциональной полноте, проверить, являются ли полными следующие системы, состоящие из одной функции:
а) f(x)
=
;
в) f(x,y,z)
=
(xy)
z((x
)
x
);
б) f(x,y)=
;
г) f(x,y,z)
=
(y~z)
x(yz).
2.48. Доказать, что единственными полными системами, состоящими из одной булевой функции от двух переменных, являются системы {x1x2} и {x1 | x2}.
2.49. Привести пример полной системы функций, состоящей из одной функции n переменных.