ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ

СБОРНИК ЗАДАЧ ПО КУРСУ

«ДИСКРЕТНАЯ МАТЕМАТИКА»

Для практических и самостоятельных занятий по специальности 061800 «Математические методы в экономике»»

Мурманск

2008

Печатается по решению редакционно-издательского совета Мурманского государственного педагогического университета

Рецензенты:

Е.Е. Маренич, доктор физ.-мат. наук, профессор (Мурманский государственный педагогический университет); Н.М. Ежова, канд. пед. наук, доцент (Мурманская академия экономики и управления)

Автор−составитель 

Н. Р. Ланина, канд. техн. наук, доцент кафедры алгебры, геометрии и прикладной математики Мурманского государственного педагогического университета

СБОРНИК ЗАДАЧ ПО КУРСУ «ДИСКРЕТНАЯ МАТЕМАТИКА» для практических и самостоятельных занятий по специальности 061800 «Математические методы в экономике»»: Методическое пособие.  Мурманск: МГПУ, 2008.  34 с.

В предлагаемых методических указаниях собраны задачи по таким разделам дискретной математики, как «Теория графов» и «Булевы функции». Выполнение упражнений, расположенных по принципу: «от простого  к сложному», позволит студентам лучше понять лекционный материал, подготовиться к контрольным работам и экзамену. Методические указания предназначены для студентов специальности 061800 «Математические методы в экономике». Они также могут помочь студентам других специальностей при изучении курса дискретной математики.

Печатается в авторской редакции

 Мурманский государственный

педагогический университет (МГПУ), 2008

Введение

Предлагаемые методические указания содержат материалы для практических занятий, индивидуальной работы со студентами и самостоятельной работы студентов при подготовке к контрольным работам по таким разделам дискретной математики, как “Теория графов” и “Булевы функции”.

Настоящие указания позволят студенту приобрести навыки в решении задач дискретной математики, глубже понять теоретический материал, а также расширить знания, полученные на лекциях.

Часть I. Графы

1.1. Подбирается экипаж космического корабля из трёх человек: командира, инженера и врача. Имеются 4 кандидата на должность командира к1, к2, к3, к4, 3 кандидата на должность инженера и1, и2, и3 и 3 кандидата на должность врача в1, в2, в3. Известно, что к1 психологически совместим с и1, и3, в2, в3; к2  с и1, и2, в1, в2, в3; к3  с и1, и2, в1, в3; к4  с и1, и2, и3, в2. Кроме того, и1 психологически несовместим с в3, и2  с в1, и3  с в2.

Сколькими способами может быть составлен экипаж?

Определение графа

1.2. Составить множество Е_i и нарисовать диаграмму неориентированного графа F_i(V, E_i), где V = {1, 2, 5, 6, 8}, а E_i  множество двухэлементных подмножеств множества V, удовлетворяющее условию:

а) Е₁ = {{a, b} / a = 2k и b = 2n; a, b  V; k, n  N};

б) Е₁ = {{a, b} / a = 2k1; a, b  V; k, n  N};

в) Е₃ = {{a, b} / a + b = 2k1; a, b  V; k  N};

г) Е₃ = {{a, b} / a, b  V}.

1.3. Составить множество Е_i и нарисовать диаграмму ориентированного графа F_i(V, E_i), где V = {0, 5, 7, 8, 10, 15}, а E_i  бинарное отношение, заданное на множестве V:

а) Е₁ = {(a, b) / a + b = 15; a, b  V};

б) Е₂ = {(a, b) / a < b; a, b  V};

в) Е₃ = {(a, b) / a  b; a, b  V};

г) Е₃ = {(a, b) / a  (b+1) = 0; a, b  V}.

Полные и однородные (регулярные) графы

1.4. Граф F  полный неориентированный и имеет n вершин. Скольким рёбрам инцидентна вершина в графе F? Сколько всего рёбер содержит граф F?

1.5. На плоскости имеется 87 точек. Сколько существует отрезков с концами в этих точках?

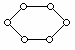
1.6. Сколько рёбер надо добавить к графу, чтобы он стал полным (рис. 1.1)?

Рис. 1.1.

1.7. Сколько диагоналей в выпуклом 92-угольнике?

1.8. Существует ли полный неориентированный граф, имеющий

а) 107 рёбер? б) 120 рёбер?

1.9. Можно ли устроить такой тренировочный турнир, чтобы в нём участвовало 33 команды, и каждая команда сыграла ровно 3 матча?

1.10. В компании из n человек у каждого ровно трое друзей. Докажите, что n чётно.

1.11. Доказать, что если каждый из 5 человек переписывается ровно с двумя другими, то не найдется трёх человек, которые все переписываются между собой.

Изоморфные графы

1.12. Доказать, что графы изоморфные (рис. 1.2).

1.13. Нарисуйте диаграммы всех неизоморфных неориентированных графов

а) с 3 вершинами (их четыре); б) с 4 вершинами (их 11).

1.14. Доказать, что все полные графы с n вершинами изоморфны.

Рис. 1.2.

1.15. Доказать, что графы не являются изоморфными (рис. 1.3).

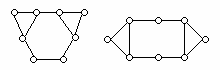
Рис. 1.3.

1.16. Исследовать графы на изоморфизм (рис. 1.4).

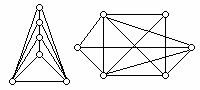
Рис. 1.4.

1.17. Доказать, что изоморфизм графов представляет собой отношение эквивалентности.

Количество графов на N помеченных вершинах

1.18. Сколько существует неориентированных графов с 5 помеченными вершинами (т.е. среди этих графов могут быть и изоморфные) и

а) 3 ребрами; б) не более чем с 3 ребрами;

в) с произвольным количеством ребер; г) 8 ребрами;

д) не менее чем с 8 ребрами; е) хотя бы с одним ребром?

1.19. Сколько существует ориентированных графов с 4 помеченными вершинами (т.е. среди этих графов могут быть и изоморфные) и

а) 10 ребрами; б) не менее чем с 10 ребрами;

в) с произвольным количеством ребер; г) 3 ребрами;

д) не более чем с 3 ребрами; е) хотя бы с одним ребром?

1.20. Известно, что на n помеченных вершинах можно построить 990 различных неориентированных графов с 2 рёбрами. Определить n.

Операции над графами

1.21. Нарисуйте граф, являющийся дополнением к графу:

а) изображенному на рис. 1.2, а;

б) изображенному на рис. 1.2, б;

в) к полному графу с 8 вершинами.

1.22. Граф F имеет 174 вершины. Скольким рёбрам инцидентна вершина в дополнении к графу F, если в F она инцидентна:

а) 173 рёбрам? б) 70 рёбрам?

1.23. Граф F называется самодополнительным, если он изоморфен своему дополнению . Нарисуйте самодополнительный граф

а) с 4 вершинами, б) с 5 вершинами.

1.24. Докажите, что количество вершин самодополнительного графа должно быть равно 4k или 4k+1, где k N.

1.25. Имеется n_i точек. Каждая пара из них соединена отрезком либо синего, либо красного цвета. Всегда ли можно выбрать из этих точек такие три, что все отрезки, соединяющие их друг с другом, будут одного цвета? а) n₁ = 4; б) n₂ = 5.

1.26. Задача Рамсея. Доказать, что среди любых шести человек найдутся либо трое попарно знакомых, либо трое попарно незнакомых.

1.27. Пусть каждая пара из 6 точек соединена отрезком либо синего, либо красного цвета. Всегда ли можно найти два треугольника, образованных отрезками одного цвета (разрешается, чтобы эти треугольники имели общую сторону)?

1.28. На географическую карту нанесено 5 городов. Из любых трех найдутся 2 города, соединенные авиалиниями, и два  несоединенные. Доказать, что

а) каждый город соединен только с двумя городами;

б) вылетев из любого города, можно облететь остальные, побывав в каждом по одному разу, и вернуться назад.

1.29. Над графами F₁ и F₂ (рис. 1.5) выполнить операции объединения F₁  F₂, соединения F₁ + F₂, произведения F₁  F₂ , композиции F₁ [F₂] и F₂ [F₁].

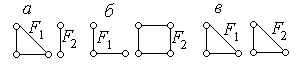
Рис. 1.5.

1.30. Пусть F₁ и F₂  полные неориентированные графы с 4 и 5 вершинами соответственно. Подсчитать количество вершин и рёбер в графах F₁F₂, F₁+F₂, F₁F₂, F₁ [F₂] и F₂ [F₁].

1.31. Доказать или опровергнуть: если F₁ и F₂  однородные графы, то таковы же графы:

а) F₁ + F₂; б) F₁  F₂; в) F₁ [F₂].

1.32. Доказать или опровергнуть:

а) = +; б) = ; в) = [].

Степени вершин графа

1.33. Существует ли полный неориентированный граф с 5 вершинами, степени которых все различны между собой, т.е. равны 0, 1, 2, 3, 4?

1.34. Нарисуйте неориентированный граф с 5 вершинами, у которого ровно 2 вершины имеют одинаковую степень.

1.35. Все вершины неориентированного графа F(V, E) (|V| = n, |E| = m) имеют степень k или k+1. Доказать, что если F имеет n_k вершин степени k и n_k+1 вершин степени k+1, то n_k = (k+1)n  2m.

1.36. Доказать, что в любом неориентированном графе количество вершин нечётной степени чётно.

1.37. В тренировочном турнире участвовало 12 команд, причём между каждыми двумя командами было сыграно по 3 матча. Сколько всего было проведено матчей?

1.38. Если в неориентированном графе с 5 вершинами ровно 2 вершины имеют одинаковую степень, то могут ли они обе быть изолированными или обе иметь степень 4?

1.39. Доказать, что в любой компании, состоящей из 11 человек, найдутся 2 человека, имеющих одинаковое количество знакомых в этой компании.

1.40. Во всякой ли компании найдутся 3 человека, у которых одинаковое количество знакомых в этой компании?

Способы задания псевдографов

1.41. Для псевдографа, изображённого на рисунке 1.6, а, составить матрицу смежности, матрицу инцидентности, список рёбер, списки смежности. Определить степени всех его вершин.

1.42. Для графа, изображённого на рисунке 1.6, б, составить матрицу смежности, матрицу инцидентности, список рёбер, списки смежности. Определить степени всех его вершин.

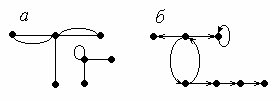
Рис. 1.6.

1.43. Без помощи диаграммы по известной матрице инцидентности неориентированного псевдографа восстановить его список ребер и матрицу смежности.

а б в

1	0	1	0	0		1	1	0	0	0	0		1	1	0	0	0
1	0	0	0	1		1	0	1	0	0	0		1	0	0	1	0
1	0	0	0	1		1	0	0	1	0	0		1	0	0	0	1
0	1	1	0	0		0	0	0	0	0	1		0	1	1	0	0
0	1	0	0	1		0	1	0	1	0	0		0	0	0	1	1
0	1	0	0	0		0	0	1	0	1	0		0	0	0	1	1
0	0	1	0	0		0	0	1	0	1	0		0	0	0	1	1
0	0	0	1	1		0	0	1	0	0	1		0	0	1	0	0

1.44. Без помощи диаграммы по известной матрице инцидентности ориентированного псевдографа восстановить его список ребер и матрицу смежности.

а б в

1	0	0	1	0		1	0	0	1	0	0		1	0	1	0	0
2	0	0	0	0		0	1	0	1	0	0		1	0	0	1	0
1	1	0	0	0		0	1	0	0	0	1		1	0	0	0	1
0	1	0	0	1		0	2	0	0	0	0		0	0	1	0	1
0	0	1	0	1		1	0	1	0	0	0		1	0	0	1	0
1	0	0	0	1		0	1	0	1	0	0		0	1	0	1	0
0	1	0	0	1		0	0	0	1	1	0

1.45. Без помощи диаграммы по известной матрице смежности неориентированного псевдографа восстановить его матрицу инцидентности и определить степени всех вершин.

а б в

0	1	0	2	0		0	0	1	0	0	0		0	1	1	0	1
1	0	1	0	0		0	0	0	0	2	1		1	0	1	1	0
0	1	0	1	0		1	0	1	0	0	1		1	1	1	0	0
2	0	1	1	1		0	0	0	0	1	0		0	1	0	0	2
0	0	0	1	0		0	2	0	1	0	3		1	0	0	2	0
						0	1	1	0	3	0		0	0	0	0	0

1.46. Без помощи диаграммы по известной матрице смежности ориентированного псевдографа восстановить его матрицу инцидентности и определить степени всех вершин.

а б в

0	1	1	0	1		0	1	0	0	0	0		1	0	0	0	0
0	0	0	0	0		0	0	0	0	0	1		0	0	0	0	0
0	0	1	0	0		0	0	1	0	0	0		0	1	0	0	0
1	0	0	1	0		0	0	0	0	0	0		0	1	0	0	3
0	0	2	1	0		0	1	0	0	0	0		1	0	1	0	0
						1	1	0	1	0	0

1.47. Без помощи диаграммы по известному списку рёбер ориентированного псевдографа восстановить его матрицу инцидентности и матрицу смежности, а также определить степени всех вершин.

a	b	c	d	e	f	g	h
1	1	1	3	3	4	4	5
2	5	6	3	6	3	5	4

1.48. Пусть C^r обозначает r-ю степень матрицы смежности ориентированного псевдографа F. Доказать, что (i, j)-й элемент матрицы C^r равен количеству всех путей длиной r из _i в _j.

1.49. Пользуясь утверждением задачи 1.48, по заданной матрице C смежности ориентированного псевдографа F определить

а) количество путей длины 2 из вершины 1 в вершину 5;

б) количество путей длины 3 из вершины 1 в вершину 4;

в) количество циклов чётной длины l (l  4), проходящих через вершину 1.

0	1	1	1	0
1	0	1	0	1
1	1	0	1	1
1	0	1	0	1
0	1	1	1	0

Связность. Достижимость

1.50. Для псевдографа, изображённого на рисунке 1.6, а, составить матрицу отношения связности.

1.51. Для псевдографа, изображённого на рисунке 1.6, б, составить матрицу отношения достижимости. Разбить множество его вершин на классы эквивалентности.

1.52. Доказать, что в неориентированном псевдографе из всякого цикла можно выделить простой цикл.

1.53. Замкнутый путь, в котором все дуги попарно различны, называется контуром. Контур, в котором для каждой вершины  справедливо равенство ₁() = ₂() = 1, называется простым. Доказать, что в ориентированном псевдографе из всякого замкнутого пути можно выделить простой контур.

1.54. Для графа, изображённого на рис. 1.7, указать все точки сочленения и все мосты.

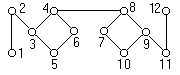
Рис. 1.7.

1.55. Всегда ли компанию из n человек, в которой у каждого ровно трое знакомых, можно разбить на n / 2 пар так, чтобы люди в каждой паре были друзьями?

1.56. Доказать, что вершина  является точкой сочленения графа F тогда и только тогда, когда в F найдутся такие вершины u и , отличные от , что  принадлежит любой простой (u, )-цепи.

1.57. Доказать, что если   точка сочленения в графе F, то она не является точкой сочленения в .

1.58. Доказать, что если неориентированный граф F не является связным, то связно его дополнение .

Эйлеровы и гамильтоновы графы

1.59. Какой из графов является эйлеровым или гамильтоновым (рис. 1.8)?

Рис. 1.8.

1.60. Выписать все эйлеровы цепи графа F, изображенного на рис. 1.9 (их восемь). Показать, что в F нет эйлерова цикла, а в подграфе F* с множеством вершин {1, 2, 3, 4} их ровно два. Доказать, что ни F, ни F* не являются гамильтоновыми.

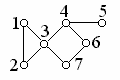
Рис. 1.9.

1.61. Проверить, существуют ли в графах, заданных матрицами смежности, эйлеровы цепи и циклы? Если “да”, то найти их.

а б

0	1	0	0	2	1		0	1	0	0	2	1
1	0	1	0	0	2		1	0	1	0	0	2
0	1	0	2	0	1		0	1	0	2	0	1
0	0	2	0	1	1		0	0	2	0	1	1
2	0	0	1	0	1		2	0	0	1	0	0
1	2	1	1	1	0		1	2	1	1	0	0

1.62. Составить маршрут для автотуристов так, чтобы каждый населенный пункт (рис. 1.10) посещался бы в точности один раз.

Рис. 1.10.

1.63. Какой из графов обязательно содержат гамильтонов цикл:

а) плоский, б) эйлеров, в) полный, г) связный?

1.64. Сколько различных гамильтоновых a) цепей, б) циклов содержит полный ориентированный граф, имеющий n вершин?

1.65. Сколько различных гамильтоновых a) цепей, б) циклов содержит полный неориентированный граф, имеющий n вершин?

1.66. Доказать, что эйлеров граф не содержит мостов.

1.67. Доказать, что если в неориентированном графе F с n  3 вершинами для любой пары несмежных вершин  и  выполняется соотношение: ()+()  n, то F гамильтонов.

1.68. Доказать, что если в неориентированном графе F с n > 3 вершинами для любой вершины  степень ()  n/2, то F гамильтонов.

1.69. Привести пример не гамильтонова графа с n = 10 вершинами, у которого ()+()  n  1 для любой пары несмежных вершин  и .

Дерево, лес. Свойства деревьев

1.70. Нарисовав диаграммы неизоморфных деревьев, показать, что

а) на 6 вершинах их шесть; б) на 7 вершинах их одиннадцать.

1.71. Доказать, что лес, состоящий из k деревьев и содержащий n вершин, имеет nk рёбер.

1.72. Сколько рёбер следует удалить из связного графа F, имеющего m рёбер и n вершин, чтобы получить дерево, содержащее все вершины F?

1.73. Из дерева Т удалено не концевое ребро. В результате образовался новый граф Т*. Доказать, что Т*  лес.

1.74. Какое максимальное и какое минимальное число концевых вершин может иметь дерево, обладающее 9-ю вершинами?

1.75. Пусть F₁  неориентированное дерево с 4 вершинами, а F₂  полный неориентированный граф с 3 вершинами. Подсчитать количество вершин и рёбер в графах F₁F₂, F₁+F₂, F₁F₂, F₁ [F₂] и F₂ [F₁].

1.76. С помощью алгоритма Прюфера восстановите по вектору дерево. Сделайте проверку.

а) (3, 3, 7, 1, 1, 1); в) (7, 11, 11, 6, 6, 6, 2, 2, 10, 1);

б) (1, 2, 2, 4, 9, 5, 5, 5); г) (2, 3, 1, 4, 4, 4, 1, 2, 6, 6).

1.77. В дереве с n концевыми вершинами нет вершин степени 2 (исключение может составлять только корень). Доказать, что общее число вершин такого дерева не превосходит 2n1.

Двудольный граф

1.78. Показать, что дерево является двудольным графом.

1.79. Показать, что граф, изображенный на рис. 1.11, а является двудольным и составить его матрицу смежности.

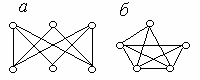
Рис. 1.11.

1.80. Охарактеризовать матрицу смежности произвольного двудольного графа.

1.81. Доказать, что наибольшее число рёбер у графов, имеющих n вершин и не содержащих треугольников, равно [n²/4].

1.82. Доказать, что граф F с n вершинами не является двудольным, если он имеет более n²/4 ребер.

1.83. Доказать, что если в графе F с n вершинами отсутствуют циклы нечетной длины и число ребер превышает (n1)²/4, то граф связный.

1.84. Доказать или опровергнуть: если F₁ и F₂  двудольные графы, то таковы же графы: а) F₁ + F₂; б) F₁  F₂; в) F₁ + [F₂].

1.85. Доказать, что граф F двудольный тогда и только тогда, когда для любого нечетного числа n все диагональные элементы матрицы Сⁿ равны нулю (С  матрица смежности графа F).

Планарность. Плоский граф

1.86. Доказать, что графы планарные (рис. 1.11) и проверить для них формулу Эйлера.

1.87. Существует ли граф с 4 вершинами, не являющийся планарным?

1.88. Является ли планарным граф, который может быть изображен проволочной моделью куба?

1.89. Неориентированный граф задан матрицей смежности. Является ли он планарным?

а б

0	1	0	0	1	1	0	0	0	0		0	1	0	0	1	1	0	0	0	0
1	0	1	0	0	0	1	0	0	0		1	0	1	0	0	0	1	0	0	0
0	1	0	1	0	0	0	1	0	0		0	1	0	1	0	0	0	1	0	0
0	0	1	0	1	0	0	0	1	0		0	0	1	0	1	0	0	0	1	0
1	0	0	1	0	0	0	0	0	1		1	0	0	1	0	0	0	0	0	1
1	0	0	0	0	0	0	1	1	0		1	0	0	0	0	0	1	0	0	1
0	1	0	0	0	0	0	1	0	1		0	1	0	0	0	1	0	0	1	0
0	0	1	0	0	1	1	0	0	0		0	0	1	0	0	0	0	0	1	1
0	0	0	1	0	1	0	0	0	1		0	0	0	1	0	0	1	1	0	0
0	0	0	0	1	0	1	0	1	0		0	0	0	0	1	1	0	1	0	0

1.90. Проверить формулу Эйлера для графа, образованного 88 квадратными полями шахматной доски. Обобщить результат на случай доски ll.

1.91. Привести пример такого графа F с 8 вершинами, что графы F и одновременно планарные.

1.92. Доказать, что в графе F с не менее чем 11 вершинами F и не могут быть планарные одновременно.

1.93. Доказать, что в графе F с не менее чем 9 вершинами F и не могут быть планарные одновременно.

Раскраска графа

1.94. Определить хроматические числа графов, изображённых на рис. 1.11.

1.95. Определить хроматическое число связного однородного графа степени 2 с n вершинами.

1.96. Доказать, что хроматическое число любого n-вершинного дерева (n  2) равно 2.

1.97. Доказать, что граф 2-хроматический тогда и только тогда, когда каждый его цикл имеет чётную длину.

1.98. Определить хроматическое число графа, полученного из полного n-вершинного графа удалением: а) одного ребра; б) двух рёбер; в) трёх рёбер, составляющих треугольник.

1.99. В плоскости проведено конечное число прямых линий, которые разбили эту плоскость на конечное число областей. Доказать, что достаточно два цвета для такой раскраски всех этих областей, когда любые две смежные области окрашиваются в разные цвета.

1.100. Доказать, что хроматическое число (F) графа F не превышает 1+(F), где (F)  максимальная из степеней вершин.

Остовное дерево

1.101. Привести пример графа, из которого нельзя выделить остовное дерево.

1.102. Найти минимальное остовное дерево, используя алгоритм

1) Крускала, 2) Прима (рис. 1.12).

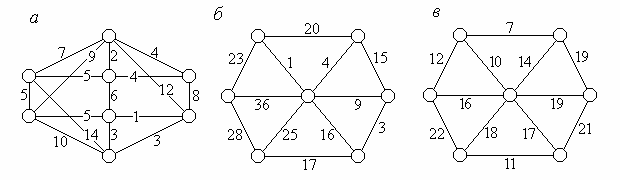
Рис. 1.12.

1.103. Доказать, что в любом нетривиальном связном неориентированном графе F есть, по крайней мере, две вершины, которые не являются точками сочленения.

1.104. Каково наибольшее число точек сочленения в графе с n вершинами?

Кратчайшие пути

1.105. Найти кратчайшие пути от вершины-источника s до всех остальных вершин как методом Форда-Беллмана, так и методом Дейкстры (рис. 1.13).

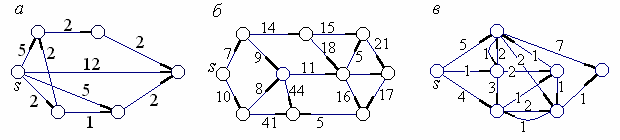
Рис. 1.13.

Максимальный поток

1.106. Перераспределить заданный начальный поток по сети так, чтобы он стал максимальным (рис. 1.14).

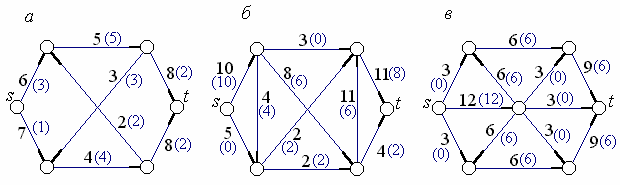
Рис. 1.14.

1.107. Найти максимальный поток в сети (рис. 1.15).

Рис. 1.15.