4. Матрицы и определители

Пример 6. Вычислить определять матрицы, разлагая его в сумму по элементам первой строки:

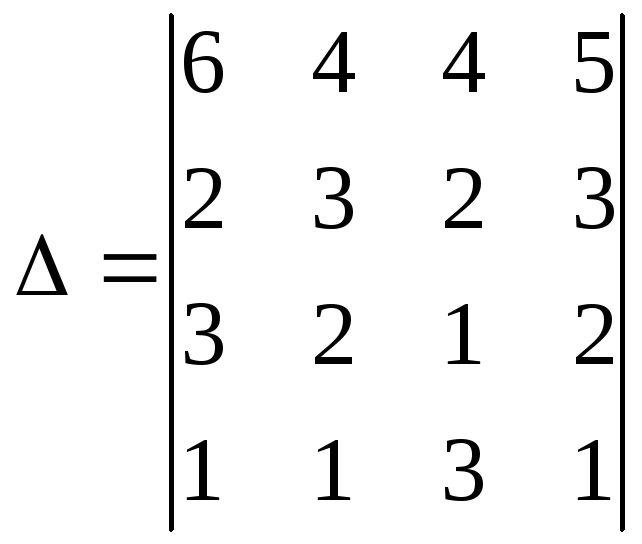
Решение.

=

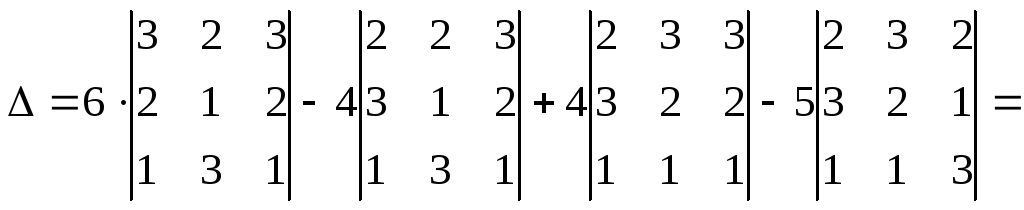
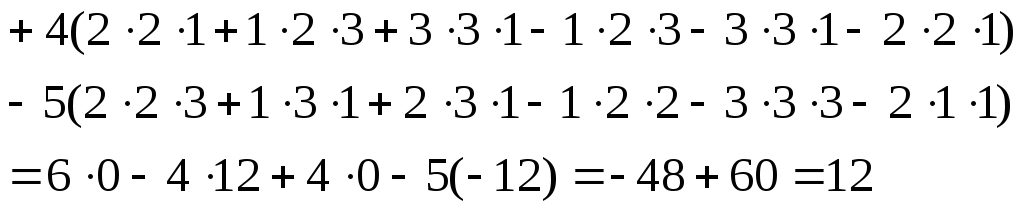
Пример 7. Дана матрица А. Выяснить является ли она невырожденной. Найти матрицу , обратную к А.

Решение. 1 4 0

А = 1 3 1

-2 4 0

1. Находим определить матрицы А:

1 4 0

1 3 1 =

-2 4 0

Значит матрица невыраженная и у нее существует обратная матрица А.

2. Находим алгебраические дополнения для каждого элемента матрицы А.

3 1 = - 4, 1 1 = -2

4 0 -2 0

1 3 = 10, 4 0 = 0

-2 4 4 0

1 0 = 0, 1 4 = -12

-2 0 -2 4

4 0 = 4, 1 0 = -1

3 1 1 1

1 4 = -1

1. 3

3. Составим матрицу из алгебраических дополнений, взятых в том же порядке, что и элементы матрицы А.

-4 -2 10

0 0 -12

4 -1 -1

4. Транспонируем матрицу , т.е. поменяем ролями строки и столбцы, получим матрицу :

- 4 0 4

= -2 0 -1

10. -12 -1

5. Разделим каждый элемент матрицы на определитель. Получим обратную матрицу .

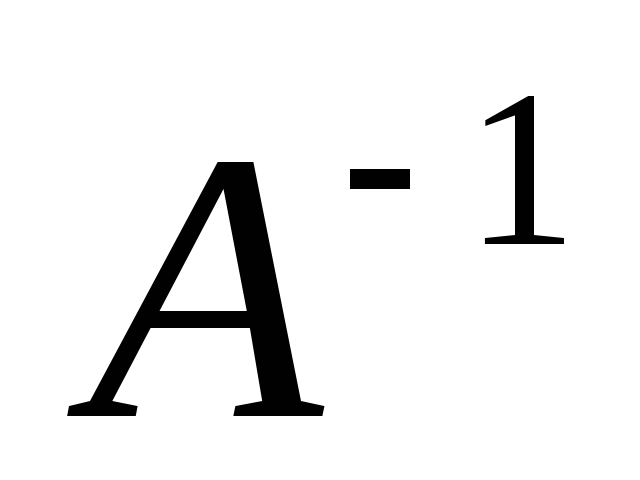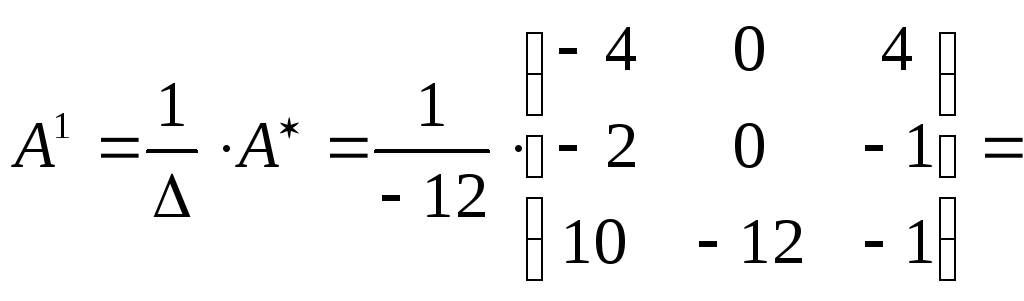
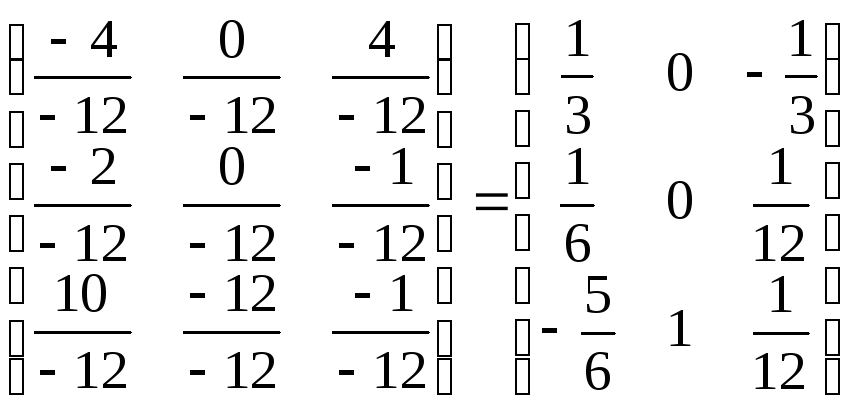
Проверка:

1 4 0 0 1 0 0

1 3 1 0 = 0 1 0 = E

-2 4 0 1 0 0 1

5. Системы линейных алгебраических уравнений

Пример 8. Проверить совместность системы уравнений и в случае совместности решить ее:

а) по формулам Крамера;

б) с помощью обратной матрицы (матричным методом);

в) методом Гаусса.

Решение. Совместность данной системы проверим по теореме Кронекера-Капелли. С помощью элементарных преобразований расширенную матрицу приведем к трапециевидной формуле:

1 2 -1 6 1 2 -1 6 1 2 -1 6

= 2 -1 1 -1  0 -5 3 -13  0 -5 3 -13

3 1 5 0 0 -5 8 -18 0 0 5 -5

Следовательно, rangA = rang=3 (числу неизвестных системы). Значит, исходная система совместна и имеет единственное решение.

а) по формуле Крамера:

где

1 2 -1

2 -1 1 = -25;

3 1 5

6 2 -1 1 6 -1 1 2 6

-1 -1 1 = -25; 2 -1 1 = - 50; 2 -1 -1 = 25.

0 1 5 3 0 5 3 1 0

Находим

б) С помощью обратной матрицы где - обратная матрица к А, Н – столбец правых частей:

- 1 1 2 1 2 -1 2 -1

1 5 = - 6 ; 3 5 = - 7 ; 3 1 = 5; 1 5 = -11;

1 -1 1 2 2 -1 1 - 1

3 5 = 8; 3 1 = 5; -1 1 = 3; 2 1 = -3;

1 2

2 -1 = - 5.

Решение системы:

6 - 11 3 6 1

х = = -7 8 -3 -1 = 2

5 5 -5 0 -1

т.е.

в) Наша система эквивалентна

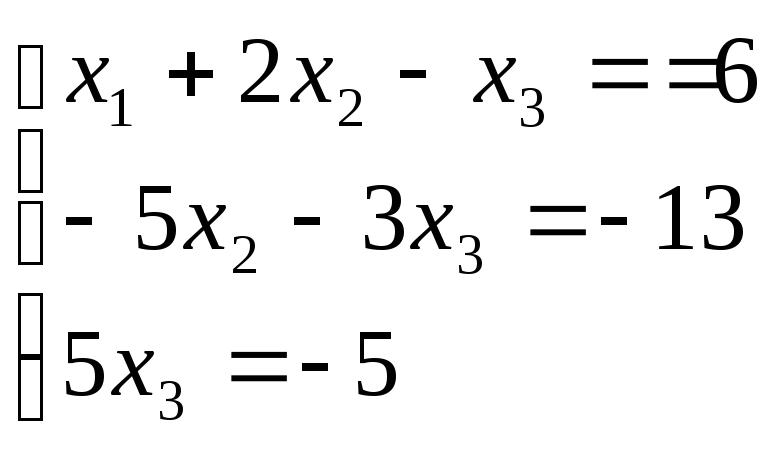
(прямой ход Гаусса совершен при нахождении рангов матриц и ) :

тогда

Пример 9. Решить однородную систему линейных алгебраических уравнений:

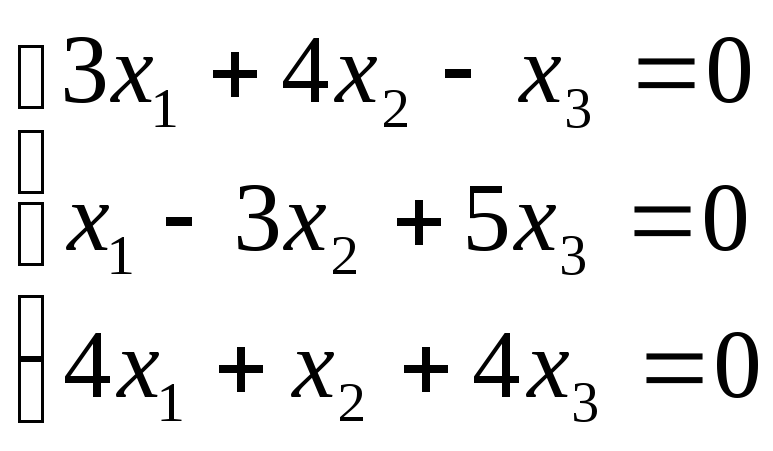
С помощью элементарных преобразований матрицу А приведем к трапециевидной форме:

3 4 -1 1 -3 5

1 -3 5  0 13 -16

4 1 4 0 0 0

Следовательно, rangA = 23 и система имеет бесконечное множество решений, зависящих от 3 – 2 = 1 произвольной постоянной. Исходная система эквивалентна

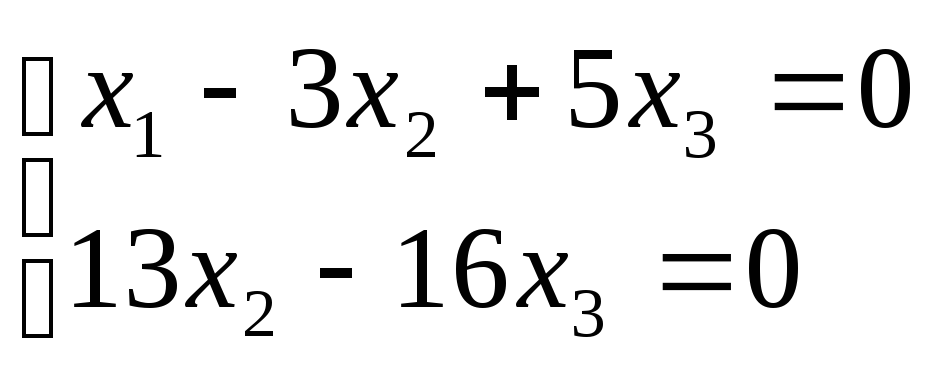
Откуда

Полагая (произвольной постоянной), имеем