2. Прямая в пространстве

22) Параметрические уравнения в прямой:

где () – точка, через которую проходит прямая, параллельно вектору

23. t – переменный параметр εR. Исключая из уравнений параметр t, получим канонические уравнения прямой:

24)Угол между двумя прямыми и находится по формуле:

=

25. Условие параллельности прямых и :

║ 

25. Условие перпендикулярности прямых и:

  = 0

3. Прямая и плоскость в пространстве

25. Угол между прямой и плоскостью

Д = 0 находится по формуле: =

25. Условие параллельности прямой и плоскости: L ║ P  A+ Bm + Cn = 0

26. Условие перпендикулярности прямой и плоскости: ║ Р 

Координаты точки пересечения находятся из системы уравнений

30)

Пример 2. Составить уравнение плоскости, проходящей через точку М (1; -3; -2) параллельно плоскости 3х-2у+4z-3=0

Решение. Ищем уравнение плоскости в виде Ах + Ву + Сz + Д = 0. Две параллельные плоскости имеют общую нормаль = (3; -2; 4). Следовательно уравнение искомой плоскости имеет вид 3х – 2у + 4z + Д = 0.

Точка М (1; -3; -2) по условию лежит в искомой плоскости. Следовательно, подставкой координат в уравнение плоскости получим тождество: Д = 0.

Отсюда находим, что Д = - 1. Уравнение искомой плоскости имеет вид 3х-2у+4z-1=0.

Пример 3. Написать уравнение плоскости, параллельной плоскости х-2у+2z+5=0 и удаленной от точки М (3; 4; -2) на расстояние d=5.

Решение. Уравнение искомой плоскости ищем в виде х – 2у + 2z + Д = 0.

Найдем значение Д. Т.к. точка М удалена от искомой плоскости на расстояние d = 5, то по формуле (18) записываем 5 = или 5 = т.е. 15 = (Д - 9) откуда Д = 24 и Д = -6. Условию задачи удовлетворяют две плоскости: х – 2у + 2z + 24 = 0, и

Х – 2у + 2z – 6 = 0.

Пример 4. Найти уравнение прямой, проходящей через точку М (-2; 3; 4) и перпендикулярной прямым и

Решение. Уравнение искомой прямой имеет вид Найдем - координаты направляющего вектора этой прямой. Используя условие перпендикулярности прямых, можно записать:

По правилу решения системы двух линейных однородных уравнений с тремя неизвестными находим:

-1 2 1 2 1 -1

t = -5t, m = - t = t, n = t = 3t, где t – число

1 3 2 3 2 1

Уравнение искомой прямой есть или

Пример 5. Найти координаты точки, симметричной точке (3; 4; 5) относительно плоскости х – 2у + z - 6 = 0.

Решение. Точка симметричная точке , относительно плоскости, находится на перпендикуляре к плоскости, находится на перпендикуляре к плоскости и является концом отрезка для которого серединой будет точка N пересечения прямой и плоскости. Направляющий вектор перпендикуляра к плоскости – это вектор-нормаль этой плоскости = (1; -2; 1). Уравнение перпендикуляра к плоскости, проведенного через точку , имеет вид

или Координаты точки N пересечения перпендикуляра с плоскостью находим, решая систему (30)

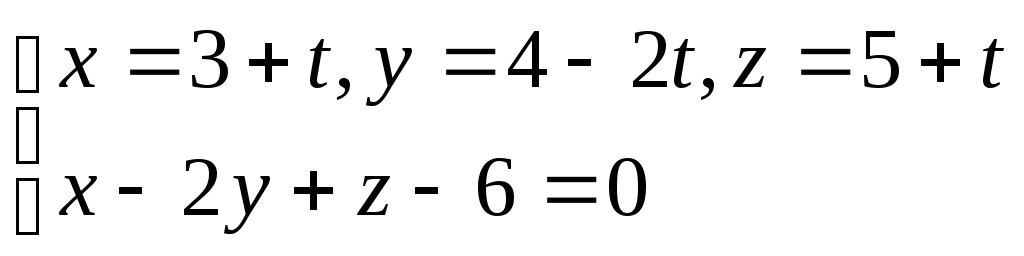
Из равенства вытекает равенство 6t – 6 =0, т.е. t = 1, следовательно х = 3 + 1 = 4; у = 4 – 2  1 = 2; z = 5 + 1 = 6, т.е. N (4; 2; 6) – точка пересечения прямой и плоскости. А так как N – середина отрезка М M, то

Имеем

,

Отсюда находим т.е. точка имеет координаты (5; 0; 7).