Учебно-методическое пособие по дисциплине «Высшей математике» для студентов-заочников 1-го курса
Составитель- разработчик: ст. преподаватель Кобяк Г.Ф. Учебно-методическое пособие по дисциплине «Высшей математике» для студентов-заочников 1 курса
Учебно-методическое рекомендовано к изданию решением кафедры математики и информатики.
1.Основные формулы.
Даны два вектора со своими координатами
и
-
тогда скалярное произведение двух векторов:
=
2.) если
,
то
;
3.) если
,
то
4)
Абсолютная величина (модуль) вектора:
5) Угол между векторами:
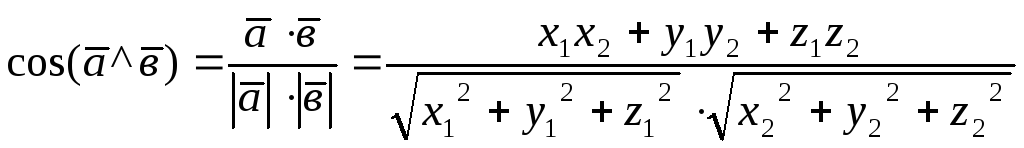
6) Общее уравнение прямой:
7) Уравнение прямой с угловым коэффициентом имеет вид:
где
(L угол наклона прямой к
оси
),
-
ордината точки пересечения прямой с
осью
.
8) Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом:
,
где
угол,
образуемый прямой с осью
);
-
координаты данной точки.
9)
Уравнение прямой, проходящей через две
данные точки
,
где
10) Нормальное уравнение прямой:
где р –
длина перпендикуляра, опущенного из
начала координат на прямую, L
– угол, который этот перпендикуляр
образует с положительным направлением
оси
11) Общее
уравнение прямой (6) можно преобразовать
в нормальное уравнение путем умножения
на нормирующий множитель
знак выбирается из условия:
12)
Расстояние от точки до прямой:
где
-
координаты точки,
нормальное уравнение прямой.
13) Угол между двумя прямыми:
находится по формуле
если
то
если
то
Пример 1. Даны вершины А (1; 1), В (7, 4), С (4, 5) треугольника.
Найти: 1) длину стороны АВ; 2) внутренний угол А; 3) уравнение высоты, опущенной из вершины С; 4) уравнение медианы, проведенной из вершины С; 5) точку пересечения высот треугольника; 6) длину высоты опущенной из вершины С; 7) определить систему линейных неравенств, определяющих внутреннюю область треугольника АВС. Сделать чертеж.
Решение:
-
Длина стороны АВ равна
=
=
=
=
=
-
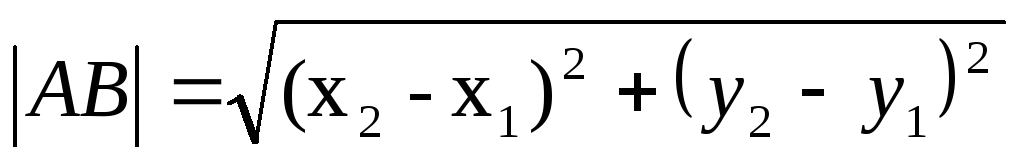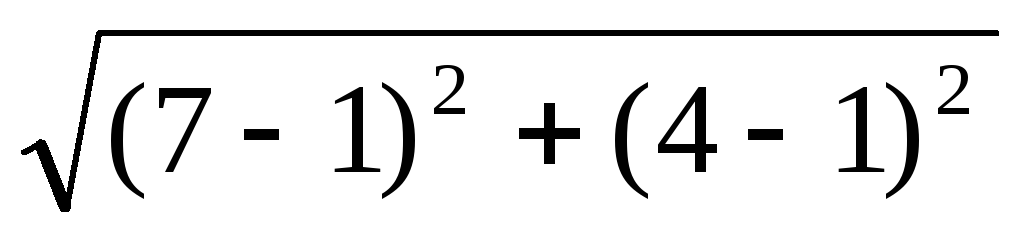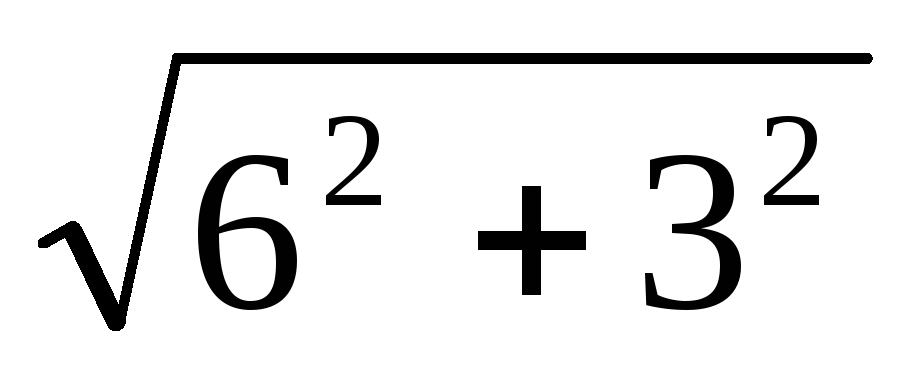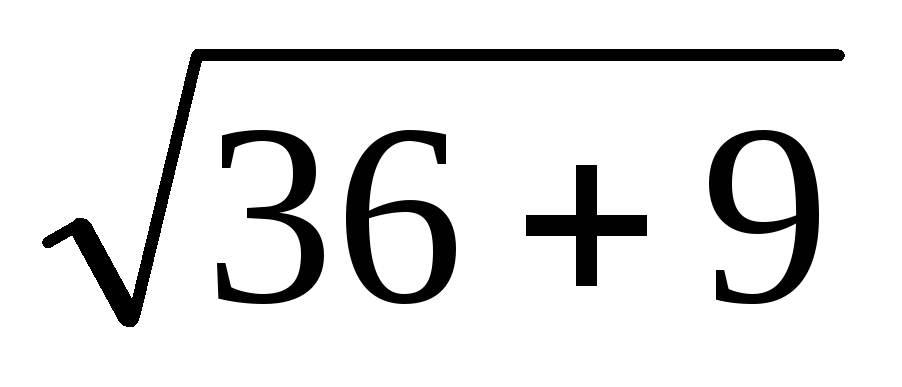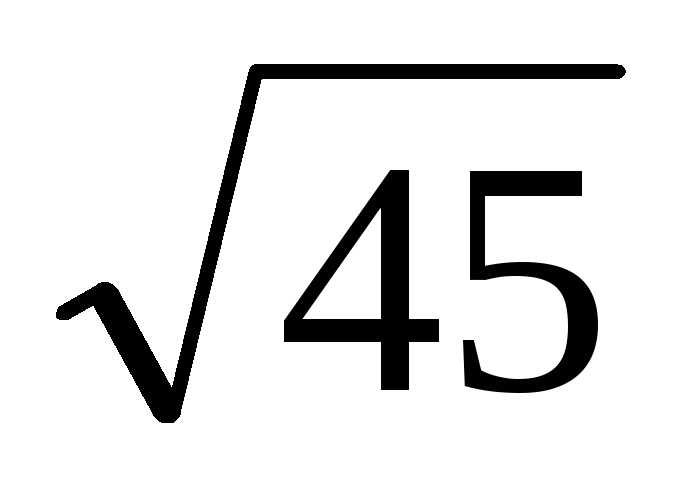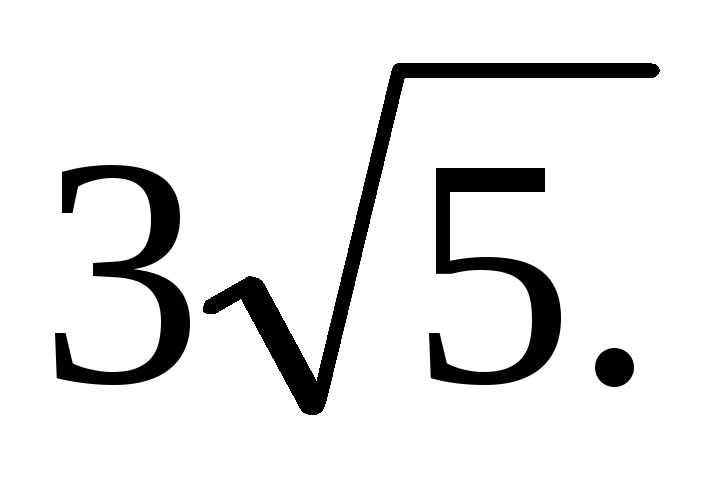
Находим угловые коэффициенты прямых АВ и АС:
Тогда
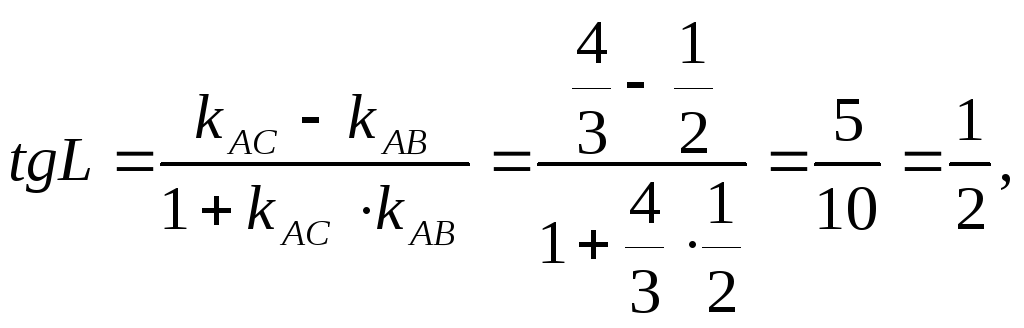
рад.
-
Пусть высота, опущенная из вершины С, пересечет прямую АВ в точке N. Прямые АВ и СN перпендикуляры, значит их угловые коэффициенты
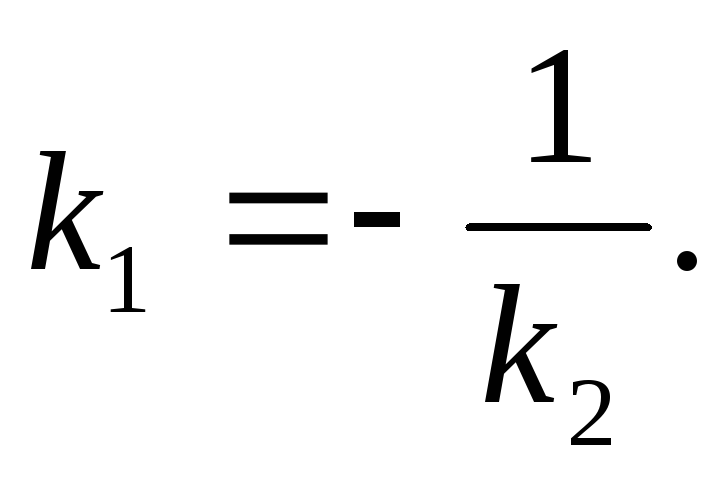
Запишем
уравнение прямой АВ:
тогда у прямой СN угловой
коэффициент будет
Уравнение
высоты СN:
4) Для
получения медианы, проходящей через
вершину С, находим координаты середины
АВ – точки М
тогда уравнение прямой СМ
или
откуда видно, что медиана параллельна оси ОУ и ее уравнение х =4.
-
Находим точку пересечения высот треугольника. Для этого напишем уравнение высоты, проходящей через точку В.
Координаты точки пересечения высот удовлетворяют системе уравнений.
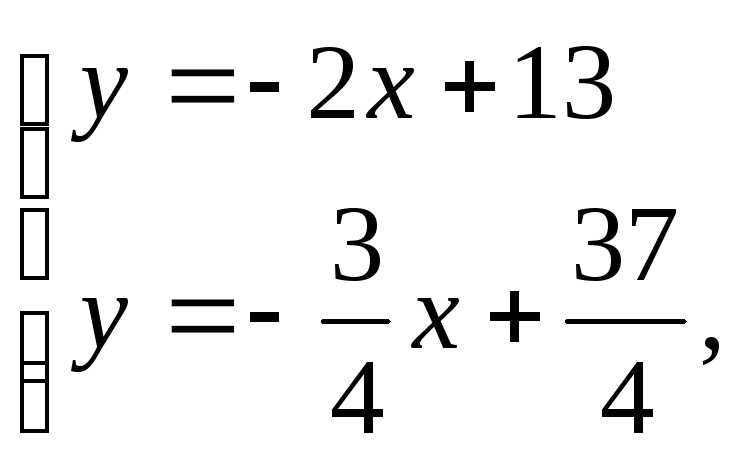откуда
-
Находим длину высоты, опущенной из вершины С. Находим координаты точки пересечения этой высоты со стороной АВ, т.е. решим систему:
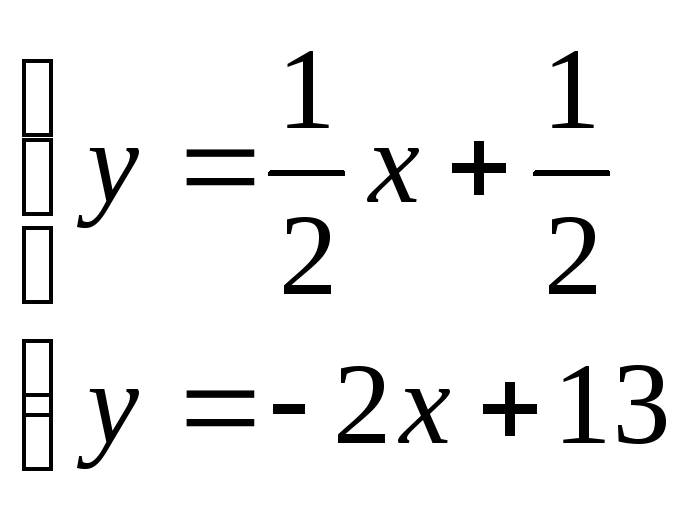
Тогда
длина высоты равна
=
=
=
-
Запишем систему линейных неравенств, определяющих внутреннюю область
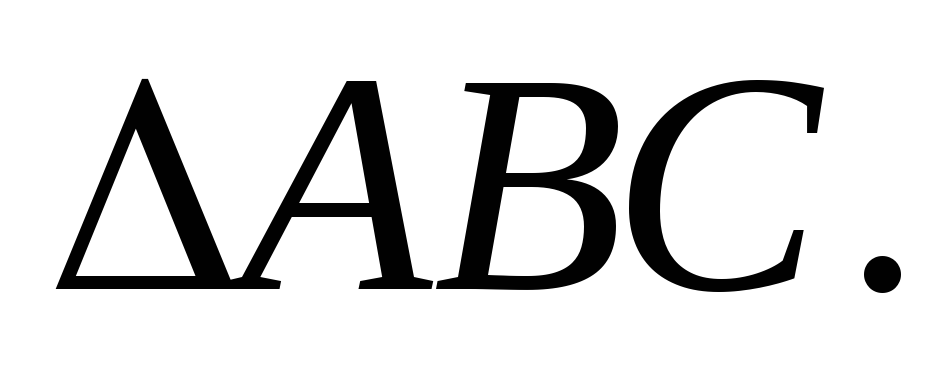Для этого надо написать уравнение
сторон треугольника:
АВ:
или
АВ:
или
АВ:
или
Прямая АВ разбивает
плоскость на две полуплоскости. Одна
из них определяется неравенством
х – 2у + 1 < 0, которому удовлетворяет
точка С:
Неравенство
Определяет полуплоскость, содержащую
точку В.
И наконец,
- это полуплоскость, содержащая точку
А.
И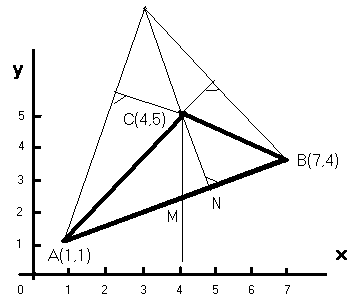
так,
искомая система неравенств, которая
определяет все точки, лежащие внутри
треугольника АВС, имеет вид:
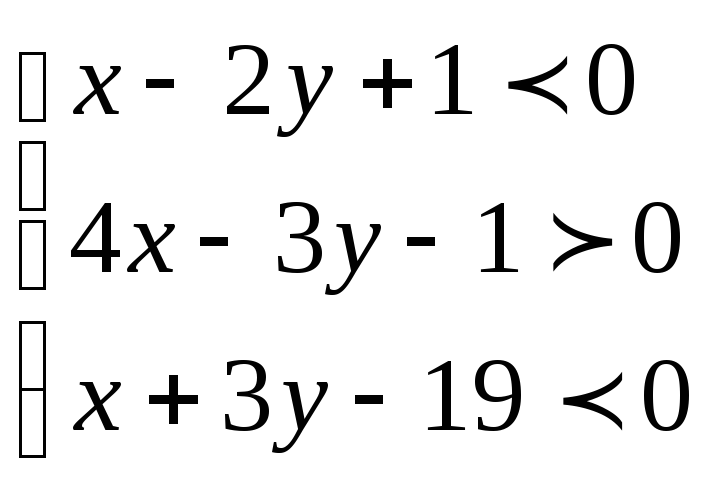
14) Уравнение плоскости,
проходящей через точку
перпендикулярно вектору
15) Общее уравнение
плоскости:
Вектор
называется нормальным вектором плоскости.
16) Уравнение плоскости в отрезках
где
-
абсцисса, ордината и аппликата точек
пересечения плоскостью координатных
осей Ох, Оу и Оz соответственно.
17) Уравнение плоскости,
проходящей через три данные точки
,
и
:
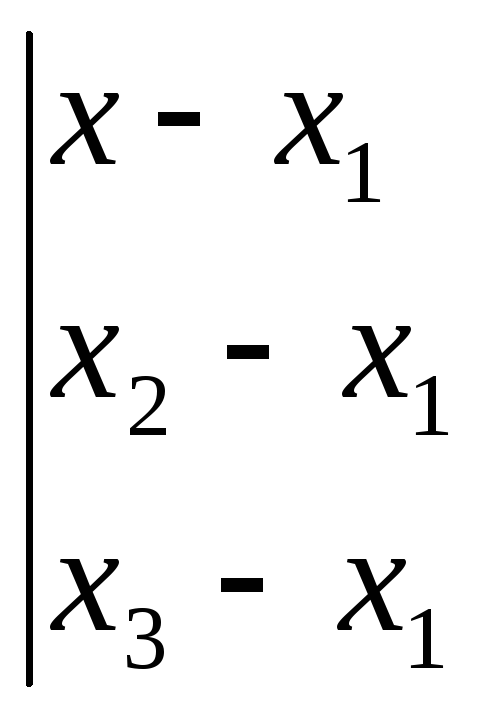
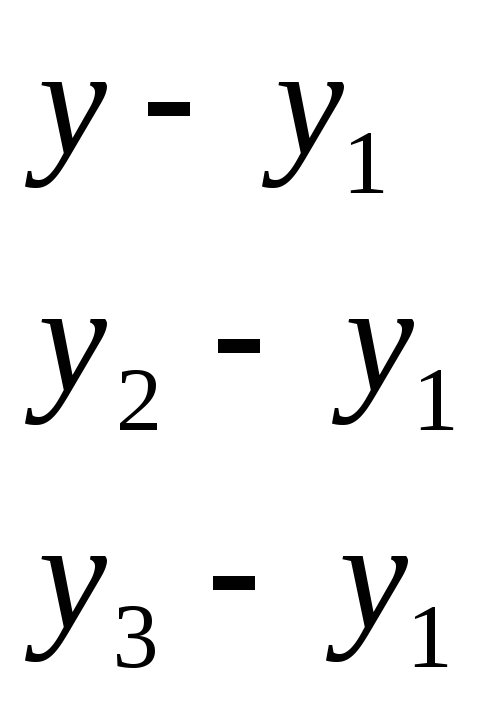
= 0
Чтобы привести общее
уравнение плоскости к нормальному виду
надо умножить его на нормирующий
множитель
, где знак
выбирается из условия
тогда:
или
где
Р = длина перпендикуляра,
опущенного из начала координат на
плоскость,
,
γ – углы образованные единичным вектором
,
имеющего направление перпендикуляра,
с осями Ох, Оу и Оz.
18). Расстояние от точки
до плоскости находится по формуле
где
данная
точка.
19). Угол между двумя плоскостями:
находится по формуле:
γ
=
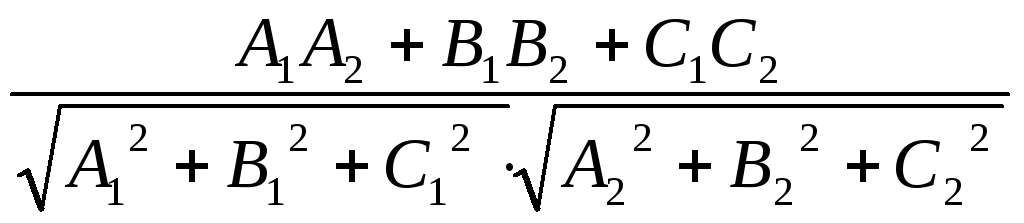
20). Условие параллельностей
и
:
-
Угловые перпендикулярности двух плоскосте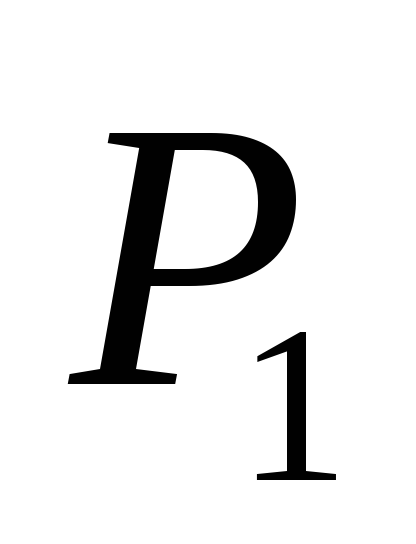й
и
:
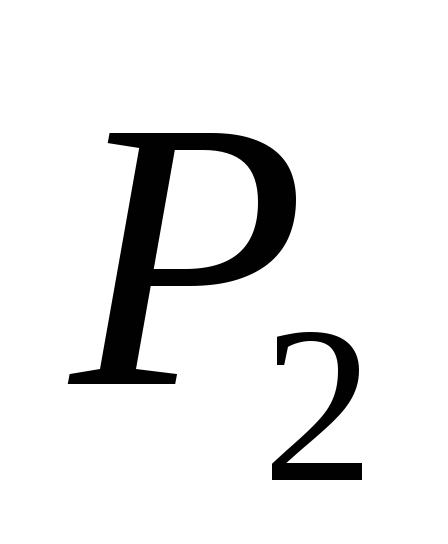