3.6. Реальное дифференцирующее звено

Передаточная функция звена

,

Построим графики ЛАЧХ и ЛФЧХ при K=5 ,К=10, К=2.5

Построим графики ЛАЧХ и ЛФЧХ при T=1 ,T=2, T=0.5

Вывод: Увеличение параметра Т приводит к уменьшению усиления по амплитуде в области высоких частот и уменьшению фазового сдвига в области асимптотического перехода. Увеличение коэффициента усиления К приводит к сдвигу вверх графика ЛАЧХ, на фазовый сдвиг параметр К не влияет.

3.7. Инерционно-форсирующее звено

Передаточная функция звена

Построим графики ЛАЧХ и ЛФЧХ при T0=5 ,T0=10, T0=2.5

Построим графики ЛАЧХ и ЛФЧХ при K=5, K=10, K=2.5

Построим графики ЛАЧХ и ЛФЧХ при T=2 ,T=4, T=1

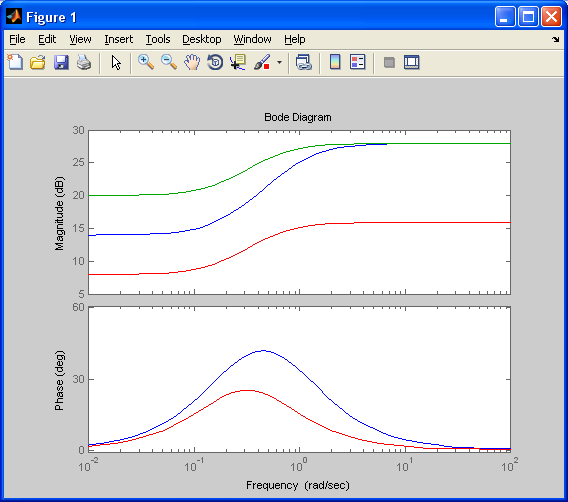
Вывод: Увеличение коэффициента усиления К приводит к сдвигу вверх графика ЛАЧХ, на фазовый сдвиг параметр К не влияет. Увеличение параметра Т₀ приводит к увеличению усиления по амплитуде в области высоких частот и увеличению фазового сдвига в области асимптотического перехода. Увеличение параметра Т, приводит к уменьшению усиления по амплитуде в области высоких частот и уменьшению фазового сдвига в области асимптотического перехода.

4. Ответы на контрольные вопросы:

1)Частотные характеристики связаны с параметрами передаточной функции следующим образом:

Пример:

Рассмотрим апериодическое звено первого порядка. Передаточная функция данного звена имеет вид . Параметр Т определяется из соотношения: , где- собственная частота колебательного звена. Это точка, в которой происходит асимптотический излом, т. е. пересекаются асимптоты из области низких и высоких частот.

Параметр К находится из соотношения , где у – точка пересечения графика ЛАЧХ с осью ординат.

2) Основная особенность построения ЛЧХ заключается в том, что приближенные (асимптотические) ЛАЧХ типовых динамических звеньев изображаются отрезками прямых. При этом под асимптотической ЛАЧХ понимается ЛАЧХ, при построении которой отдельно рассматривают области высоких (ОВЧ) и низких частот (ОНЧ) и для каждой определяют свою асимптоту.

3) Для построения АФХ надо сделать в W(s) подстановку s = jω, и тогда, полученная W(jω) является комплексным выражением

,

которое можно построить на комплексной плоскости. В этом случае конец вектора, соответствующий комплексному числу , при изменении от 0 до прочерчивает на комплексной плоскости кривую, которая и будет являться амплитудно-фазовой характеристикой (АФХ). Пример графика АФХ: