лабораторная работа / chastotnye_harakteristiki_dinamicheskih_zvenev (2)

Министерство Образования Российской Федерации

Уфимский Государственный Авиационный Технический Университет

Кафедра АСУ

Отчет по лабораторной работе №2

по предмету «Основы теории управления»

на тему: Динамические звенья и их характеристики во временной области

Вариант №1

Выполнил:

Студент

группы АСОИ-335

Проверил:

Лянцев О.Д.

Уфа 2010

1. Цель работы

Целью работы является изучение частотных характеристик типовых динамических звеньев с использованием автоматизированных средств моделирования на ПК – MATLAB,SIMULINK.

2. Теоретическая часть

Сущность метода частотных характеристик заключается в том, что на вход исследуемой системы подается гармонический сигнал (синусоидальные колебания) в широком диапазоне частот. Реакция системы при разных частотах позволяет судить о ее динамических свойствах.

Пусть входной сигнал системы имеет амплитуду а и частоту ω, т. е. описывается формулой

Выходной сигнал будет иметь амплитуду А₁ и отличаться от входного по фазе на величину ψ (фазовый сдвиг):

Таким образом, можно рассчитать усиление по амплитуде

Для каждой частоты входного сигнала ω будут свои А и ψ.

Изменяя ω в широком диапазоне, можно получить зависимость А(ω) – амплитудную частотную характеристику (АЧХ) и ψ(ω) – фазовую частотную характеристику (ФЧХ).

В практических расчетах удобно применять графики частотных характеристик, построенных в логарифмическом масштабе – логарифмические частотные характеристики (ЛЧХ).

Логарифмическая амплитудная частотная характеристика (ЛАЧХ) определяется следующим выражением:

Логарифмической фазовой частотной характеристикой (ЛФЧХ) называется график зависимости , построенный в логарифмическом масштабе частот.

Единицей L(ω) является децибел (дБ), а единицей логарифма частоты – декада. Декадой называют интервал частот, на котором частота изменяется в 10 раз. При изменении частоты в 10 раз говорят, что она изменилась на одну декаду. Ось ординат при построении ЛЧХ проводят через произвольную точку, а не через точку ω = 0. Частоте ω = 0 соответствует бесконечно удаленная точка: lgω → – ∞ при ω → 0.

Основное преимущество использования ЛЧХ заключается в том, что приближенные (асимптотические) ЛАЧХ типовых динамических звеньев изображаются отрезками прямых.

3. Выполнение работы

Вариант 1:

№	Апериод звено		Апериодич. звено 2 пор. (колеб. звено)			Интегр звено	Изодр. звено		Реальное диф. звено		Инерц.-форс Звено
	K	T [с]	K	T [с]	ξ	K	K1	K2	K	τ [с]	K	T0 [с]	T [с]
1	2	0,2	1	0,2	2,0 (0,2)	2	2	0,5	2	0,4	2	2	0,8

3.1.Апериодическое (инерционное) звено первого порядка

Передаточная функция данного звена имеет вид .

К=1

Т=0.4

Вывод: постоянная времени T определяет усиление по амплитуде в области высоких частот (w>>1/T): чем меньше Т, тем больше увеличивается амплитуда выходного сигнала. Также параметр Т прямо пропорционален сдвигу по фазе между входным и выходным сигналами. Коэффициент передачи звена К прямо пропорционален усилению по амплитуде и не влияет на фазовый сдвиг.

3.2. Апериодическое звено второго порядка.

Передаточная функция звена имеет вид

Часто используют описание звена в виде:

Т.к. все корни вещественные то следует ,что .

где - коэффициент затухания.

К=2

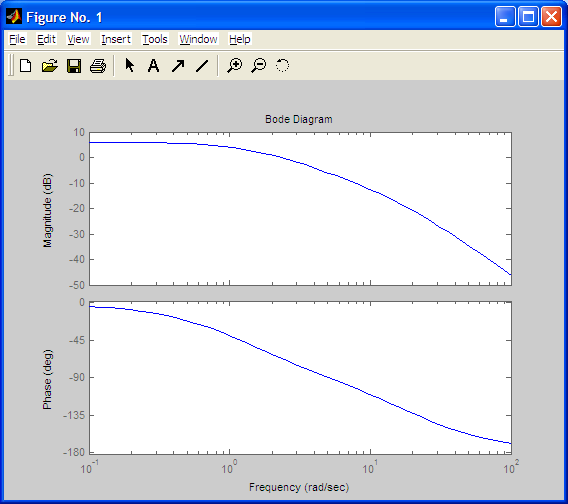
Т=0.1

Вывод: постоянная времени T определяет усиление по амплитуде в области высоких частот (w>>1/T): чем меньше Т, тем больше увеличивается амплитуда выходного сигнала. Также параметр Т прямо пропорционален сдвигу по фазе между входным и выходным сигналами, особенно это проявляется в области средних частот(w≈1/T). Коэффициент демпфирования ξ влияет на вид ЛАЧХ в области асимптотического излома. При (w<1/T) ξ прямо пропорционален фазовому сдвигу, а при (w>1/T) – обратно пропорционален. Коэффициент передачи звена К прямо пропорционален усилению по амплитуде и не влияет на фазовый сдвиг.

3.3.Интегрирующее звено

Передаточная функция звена имеет вид

К=1

К=3

Вывод: Увеличение коэффициента усиления К приводит к сдвигу вверх графика ЛАЧХ, на фазовый сдвиг параметр К не влияет.

3.4. Изодромное звено

Это звено имеет передаточную функцию

К1=1 К2=1

К1=4 К2=0.25

Вывод: Увеличение параметра К₁ приводит к увеличению усиления по амплитуде в области низких частот и увеличению фазового сдвига в области асимптотического перехода. Увеличение параметра К₂ приводит к увеличению усиления по амплитуде в области высоких частот и уменьшению фазового сдвига в области асимптотического перехода.

3.5. Реальное дифференцирующее звено

Передаточная функция звена

,

К=1 τ=0.8

Вывод: Увеличение коэффициента усиления К приводит к сдвигу вверх графика ЛАЧХ, на фазовый сдвиг параметр К не влияет. Увеличение параметра Т приводит к уменьшению усиления по амплитуде в области высоких частот и уменьшению фазового сдвига в области асимптотического перехода.

3.6. Инерционно-форсирующее звено

Передаточная функция звена

(1)

Т0=1

Т=1.6

Вывод: Увеличение параметра Т₀ приводит к увеличению усиления по амплитуде в области высоких частот и увеличению фазового сдвига в области асимптотического перехода. Увеличение параметра Т, наоборот, приводит к уменьшению усиления по амплитуде в области высоких частот и уменьшению фазового сдвига в области асимптотического перехода. Увеличение коэффициента усиления К приводит к сдвигу вверх графика ЛАЧХ, на фазовый сдвиг параметр К не влияет.

4. Ответы на контрольные вопросы:

1) Частотные характеристики связаны с параметрами передаточной функции следующим образом:

Пример:

Рассмотрим апериодическое звено первого порядка. Передаточная функция данного звена имеет вид . Параметр Т определяется из соотношения: , где - собственная частота колебательного звена. Это точка, в которой происходит асимптотический излом, т. е. пересекаются асимптоты из области низких и высоких частот.

Параметр К находится из соотношения , где у – точка пересечения графика ЛАЧХ с осью ординат.

2) Основная особенность построения ЛЧХ заключается в том, что приближенные (асимптотические) ЛАЧХ типовых динамических звеньев изображаются отрезками прямых. При этом под асимптотической ЛАЧХ понимается ЛАЧХ, при построении которой отдельно рассматривают области высоких (ОВЧ) и низких частот (ОНЧ) и для каждой определяют свою асимптоту.

3) Для построения АФХ надо сделать в W(s) подстановку s = jω, и тогда, полученная W(jω) является комплексным выражением

,

которое можно построить на комплексной плоскости. В этом случае конец вектора, соответствующий комплексному числу , при изменении от 0 до прочерчивает на комплексной плоскости кривую, которая и будет являться амплитудно-фазовой характеристикой (АФХ). Пример графика АФХ: