лабораторная работа / issledovanie_tipovyh_soedineniy_zvenev

Цель работы - исследование характеристик систем, образованных последовательным, параллельным и встречно-параллельным соединениями звеньев во временной и частотной областях.

Задание 1. Определить характеристики во временной и частотной областях последовательного соединения двух устойчивых апериодических звеньев первого порядка со следующими параметрами: к1=10; Т1=0,2N=1,2c; к2=N=6; Т2=20/N=3.33с.

Р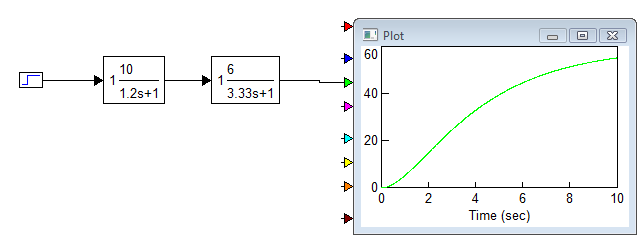ассчитать параметры к, Т,  ПФ эквивалентного звена второго порядка, записанного в виде:

Соединим два апериодических звена первого порядка последовательно.

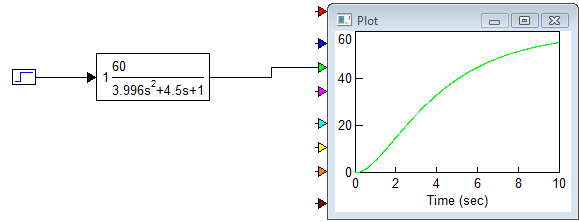
Это эквивалентное звено имеет такие же временные и частотные характеристики

Контрольные вопросы к заданию:

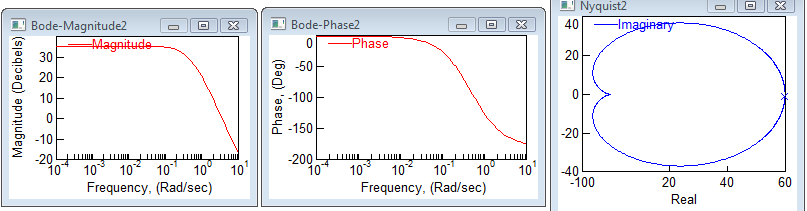
• Какой вид имеет асимптотическая ЛАЧХ соединения?

До первой сопрягающей частоты ω=1/Т₁=0,833 L(ω)=20 lgk=20 lg60=35,56, затем до второй сопрягающей частоты ω=1/Т₂=0,3 ЛАЧХ имеет наклон -20дБ/дек, после этой частоты наклон становиться -40 дБ/дек.

• Как изменяются временная и частотная характеристики апериодического звена первого порядка при последовательном включении второго звена того же типа?

Временная характеристика одного апериодического звена ; двух последовательно соединенных 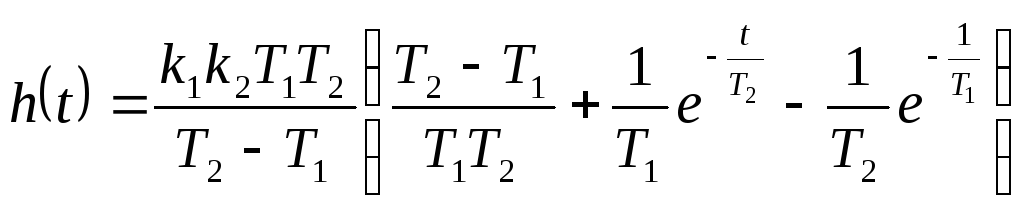. АЧХ одного звена ; двух - . ФЧХ одного звена ; двух - .

• Какое из двух звеньев оказывает основное влияние на длительность затухания переходного процесса?

Большее влияние на затухание переходного процесса оказывает то звено, у которого больше коэффициент Т. В нашем случае это второе звено.

• Является ли система второго порядка с ПФ 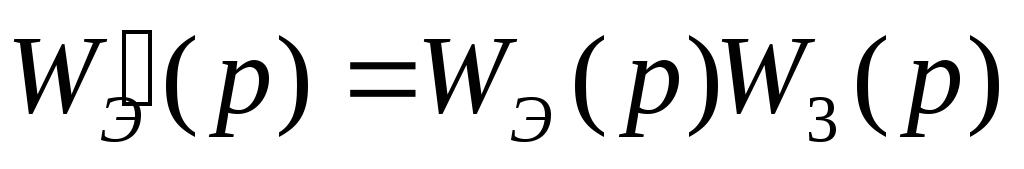полностью управляемой и наблюдаемой, если ?

Эта система не является таковой, т.к. степень числителя больше степени знаменателя.

Задание 3.2. Найти ПФ типовых звеньев, параллельные соединения которых описываются эквивалентными ДУ вида:

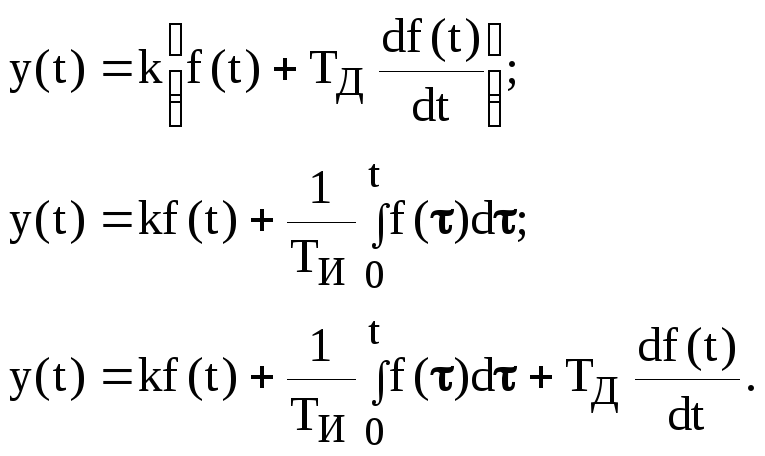
Определить характеристики эквивалентных звеньев во временной и частотной областях. Построить их асимптотические ЛАЧХ и ЛФЧХ.

Используя преобразование Лапласа, найдем передаточные функции звеньев.

Д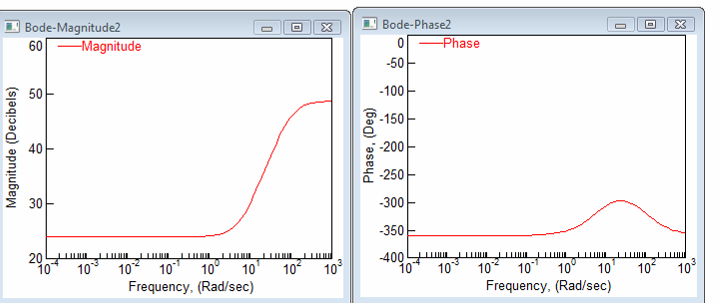 ля первого звена

Для второго звена

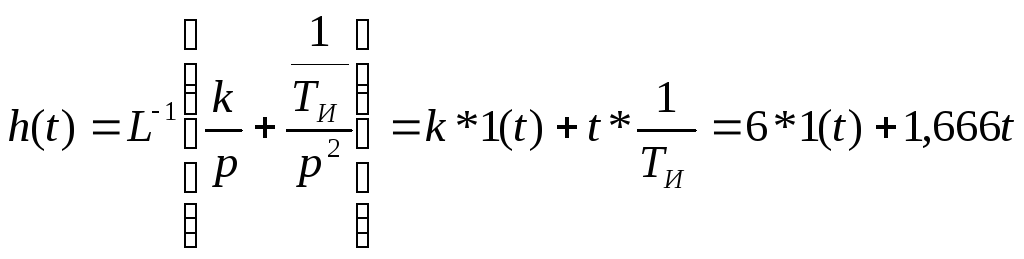
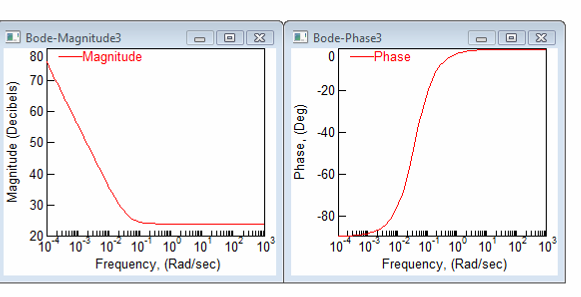
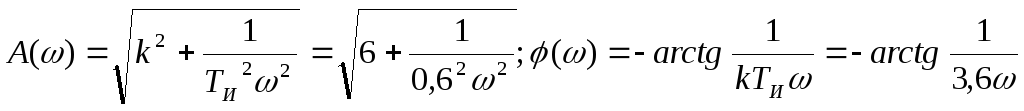
Д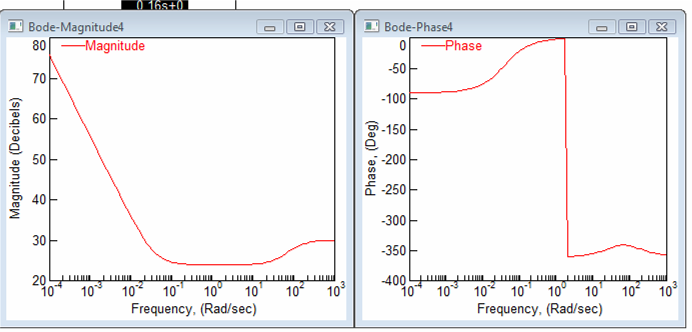 ля третьего звена

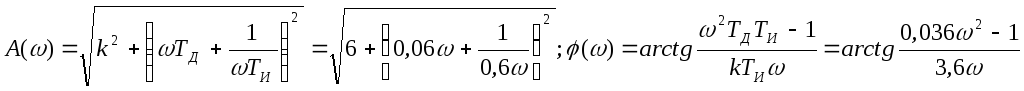
Задание 3.3. Для системы с ПФ звеньев:

Построить приближенные ЛАЧХ и ЛФЧХ замкнутой системы.

Передаточная функция системы имеет вид

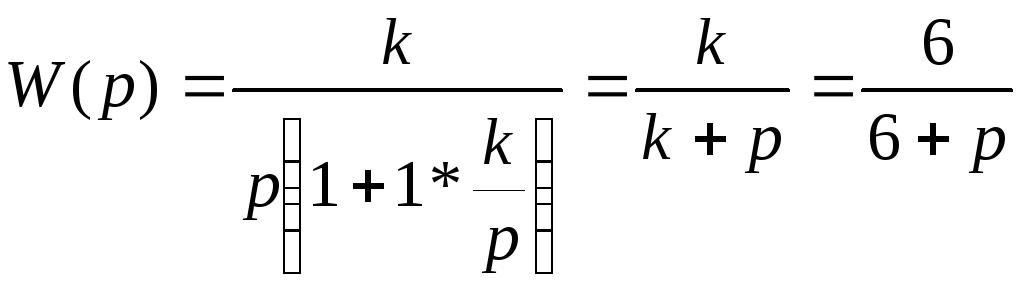
Эта передаточная функция является эквивалентной апериодическому звену первого порядка с параметрами Т=0,1666 и k=1.

Контрольные вопросы к заданию:

• Внешние сигналы какого спектра воспроизводятся системой практически без искажений?

Система воспроизводит без искажений внешние сигналы, частота которых меньше частоты среза эквивалентного апериодического звена, т.е. Гц.

• Каков спектр внешних сигналов, которые практически не пропускаются системой?

Система не пропускает сигналы с частотами большими 6Гц.

• Какому типовому звену эквивалентна замкнутая система? Каковы параметры эквивалентной ПФ?

Эта передаточная функция является эквивалентной апериодическому звену первого порядка с параметрами Т=0,1666 и k=1.

• Какой вид имеют точные ЛАЧХ и ЛФЧХ замкнутой и разомкнутой систем?

Замкнутая система:

Разомкнутая система:

Задание 3.4. Для системы, структурная схема которой имеет вид рис.2.3 с ПФ звеньев:

где Т, k – произвольные постоянные.

Переходная функция замкнутой системы будет иметь вид

Контрольные вопросы к заданию:

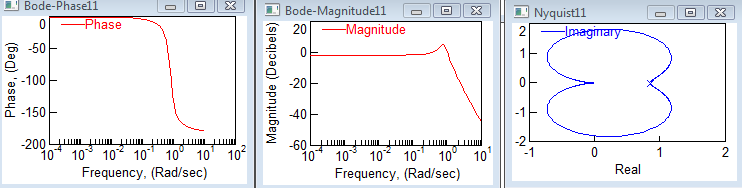
• Как выглядят ЛАЧХ, ЛФЧХ, АФХ, переходные характеристики замкнутой и разомкнутой систем, как влияет коэффициент обратной связи на основные характеристики замкнутой системы?

Замкнутая система:

Разомкнутая система:

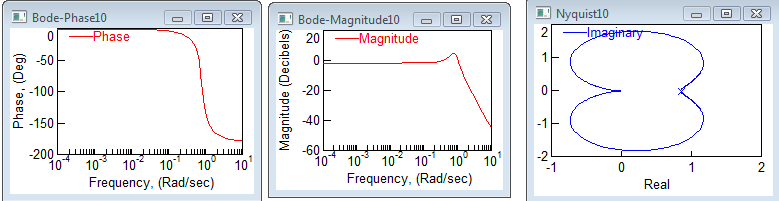
• Как изменяется переходная характеристика замкнутой системы, если коэффициент обратной связи увеличили в 2 раза; уменьшили в 2 раза?

При увеличении коэффициента обратной связи амплитуда колебаний уменьшается, при уменьшений же возрастает.

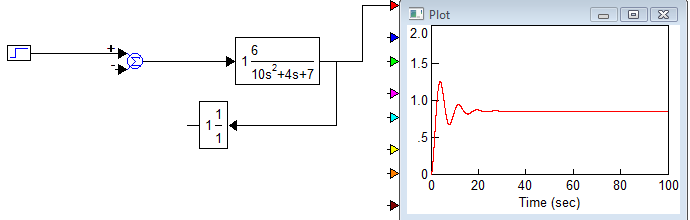
4) Вывести общую передаточную функцию для заданной структурной схемы. Необходимо построить систему в пакете Vissim, и сравнить полученные переходные процессы.

Преобразуем данную структурную схему к последовательному типу.

Где ,,

Найдем общую передаточную функцию.

Подставим численные значения в , получим:

Видим, что графики переходных процессов совпадают, значит преобразование структурной схемы было выполнено правильно.