
- •Методические указания
- •Уфа 2000
- •Методические указания
- •А б в
- •Алгебраический критерий устойчивости Гурвица
- •Тогда для устойчивости сау необходимо и достаточно, чтобы все определители имели тот же знак, что и коэффициентb0 . Частотный критерий устойчивости Найквиста
- •Лабораторная работа рс 3
- •Лабораторная работа рс-4
- •Список используемых источников
- •Приложение
МИНИСТЕРСТВА ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ УНИВЕРСИТЕТ
Методические указания
к лабораторным работам по курсу
«Управление техническими системами»
для специальности Роботы и робототехнические системы
Уфа 2000
_____________________________________________________________
Министерства образования российской федерации
Уфимский государственный авиационный университет
Кафедра технической кибернетики
Методические указания
к лабораторным работам по курсу
«Управление техническими системами»
для специальности РС
Уфа 2000
Составитель: В.А. Семеран
УДК 681.5(07)
Методические указания к лабораторным работам по курсу
«Управление техническими системами» для специальности РС/Уфимск. гос. авиац. техн. ун-т, Сост. В.А. Семеран. Уфа. 2000, - 42 с.
Содержатся описания пяти лабораторных работ, связанных с изучением динамических характеристик, исследованием устойчивости и качества переходных процессов в линейных и нелинейных САУ, а также методике синтеза САУ с использованием логарифмических частотных характеристик.
Предназначены для студентов третьего курса специальности РС, которым читается курс «Управление техническими системами».
Ил. . Табл. . Библиогр. Наимен.
СОДЕРЖАНИЕ
Стр.
Цель и задачи лабораторных работ……………………………………………5
Лабораторная работа РС-1. Исследование
характеристик типовых динамических звеньев………………………………6
Лабораторная работа РС-2. Исследование
устойчивости и точности линейных САУ……………………………………17
Лабораторная работа РС-3. Коррекция
статических и динамических свойств САУ………………………………..…23
Лабораторная работа РС-4. Синтез систем
автоматического управления методом
логарифмических характеристик…………………………………………..…30
Лабораторная работа РС-5. Исследование
автоколебательных режимов в нелинейных системах………………………36
Приложение…………………………………………………………………….41
ЦЕЛЬ И ЗАДАЧИ ЛАБОРАТОРНЫХ РАБОТ
Целью настоящих лабораторных работ является закрепление теоретических знаний и отработка навыков экспериментального исследования элементов и систем автоматического управления (САУ) на ПК. Основное внимание уделяется изучению динамических характеристик, исследованию устойчивости и качества переходных процессов в линейных САУ, методике синтеза САУ с использова- нием логарифмических частотных характеристик.
Тематика лабораторных работ соответствует утверждённой рабочей программе лекционного курса и охватывает все его основные разделы. Продолжительность каждой работы – 4 часа. Изучение и освоение используемого при выполнении лабораторных работ моделирующего пакета предполагается проводить в процессе выполнения лабораторной работы РС-1.
После выполнения каждой лабораторной работы студентами оформляется отчёт, в который включается экспериментальный и расчётный материал, полученный в процессе выполнения работы, а также делаются выводы по лабораторной работе.
ЛАБОРАТОРНАЯ РАБОТА РС - 1
ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ТИПОВЫХ ДИНАМИЧЕСКИХ
ЗВЕНЬЕВ
1. ЦЕЛЬ РАБОТЫ
Целью работы является изучение временных и частотных характеристик типовых динамических звеньев с использованием автоматизированных средств моделирования на ПК – MATLAB,SIMULINK(см. ПРИЛОЖЕНИЕ).
2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Временные характеристикидинамического звена определяются его реак-цией на входные воздействия стандартного вида при определённых начальных условиях.Переходная функцияh(t) звена – это реакция звена на единичное воз- действие1(t) при условии, что до момента приложения воздействия звено находи- лось в состоянии покоя, т.е. начальные условия были нулевыми. Подвесовой (импульснойпереходной) функцией w(t) понимают реакцию звена на единичное импульсное воздействие (t) при нулевых начальных воздействиях. В качестве примера на рис. 1.1 показаны графики переходных функций для интегрирующего и инерционного звеньев, передаточные функции которых равны соответственно
![]()
 h1(t)
h1(t)
h1(t)
h1(t)


 T
T


 h1(t)
=K1
t
h1(t)
=K1
t
 K2
K2

t t

 0 0
t3T
0 0
t3T
a b
Рис. 1.1
Частотные характеристикизвена определяют его реакцию на гармоничес- кий входной сигнал в установившемся режиме (т.е. после завершения переходных процессов).
Для динамического звена с передаточной
функцией
![]() в общем случае различают следующие
частотные характеристики:
в общем случае различают следующие
частотные характеристики:
а)
амплитудно-фазовая характеристика
(АФХ) – это график частотной передаточной
функции![]() ,
построенная на комплексной плоскости:
,
построенная на комплексной плоскости:
![]() (1.1)
(1.1)
б)
амплитудно-частотная характеристика
(АЧХ) звена определяется отношением
амплитуд выходного и входного сигналов
на частоте![]() :
:
![]() (1.2)
(1.2)
в) фазо-частотнаяхарактеристика (ФЧХ) определяет сдвиг по фазе между выходным и входным сигналами:
![]() (1.3)
(1.3)
г) логарифмическая амплитудно-частотная характеристика (ЛАХ)– это АЧХ звена, построенная в логарифмических шкалах:
![]() (1.4)
(1.4)
д) логарифмическая фазо-частотная характеристика (ЛФХ) – имеет логарифмический масштаб только по оси частот.
Построение ЛАХ типового динамического звена, как правило, сводится к построению асимптотической ЛАХ, представляющей собой совокупность отрезков прямых с наклоном, кратным 20 дб\дек. Примеры ЛАХ интегрирую- щего и инерционного звеньев приведены на рис. 1.2
 L(w),дбL(w),дб
L(w),дбL(w),дб


 20 lgK120 lgK2
3 дб
20 lgK120 lgK2
3 дб




 -20
дб/дек
-20
дб/дек
 -20 дб/дек
-20 дб/дек
wср=K1wср=K/T



0lgw, дек 0 wс=1/T lgw, дек
а б
Рис. 1.2
Типовые динамические звенья можно разделить на 3 группы: позиционные, интегрирующие идифференцирующие.
2.1. Позиционные звенья
2.1.1. Апериодическое (инерционное) звено первого порядка.
Передаточная функция данного звена, как отмечалось выше, имеет вид
![]() (1.5)
(1.5)
Переходная функция h(t) (рис. 1.1, б):
![]() (1.6)
(1.6)
Постоянная времени T переходной функцииh(t) определяет наклон касательной в начале кривой, т.е. величинаT характеризует степень инерционности динамического звена.
Амплитудно-фазовая характеристика звена (рис. 1.3)
![]() (1.7)
(1.7)
Амплитудно-частотная характеристика (рис. 1.4, а)
![]() , (1.8)
, (1.8)
фазо-частотная характеристика (рис. 1.4, б)
![]() . (1.9)
. (1.9)
Логарифмическая амплитудно-частотная характеристика имеет вид
![]() (1.10)
(1.10)
Низкочастотная асимптота (при w=0) этой характеристики имеет уравнение
![]() (1.11)
(1.11)
а высокочастотная
асимптота (при
![]() )
имеет уравнение
)
имеет уравнение
![]() (1.12)
(1.12)
Асимптотическая
(сплошная линия) и точная (штриховая
линия) ЛАХ данного звена изображена на
рис. 1.2, б. Максимальная разница (ошибка)
между асимптотической и точной ЛАХ
имеет место на частоте сопряжения
![]() и равна3 дб. Частота
срезаwсрравнаK/T
(L(wср
)=0). Наклон низкочастотной асимптоты
равен 0 дб/дек, а высокочастотной - (-20)
дб/дек.
и равна3 дб. Частота
срезаwсрравнаK/T
(L(wср
)=0). Наклон низкочастотной асимптоты
равен 0 дб/дек, а высокочастотной - (-20)
дб/дек.
 Im
Im

 K
K





 Re
Re
w=∞ w=0
 A
A
w
Рис. 1.3
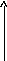 A
w=1/T
A
w=1/T




 K w,
с-1
K w,
с-1
![]()





 w, с-1
w, с-1 ![]()
 0w=1/T
0w=1/T ![]()
аб
Рис. 1.4
2.1.2. Апериодическое звено второго порядка.
Передаточная функция звена имеет вид
![]() (1.13)
(1.13)
где
![]() - коэффициент затухания.
- коэффициент затухания.
Эта передаточная функция может быть записана также в виде
![]() (1.14)
(1.14)
г![]()


 деT1иT2соответствующие постоянные времени,
определяемые корнями характеристического
уравнения
деT1иT2соответствующие постоянные времени,
определяемые корнями характеристического
уравнения
АФХ, АЧХ и ФЧХ данного звена равны:
![]() (1.15)
(1.15)
![]() (1.16)
(1.16)
![]() (1.17)
(1.17)
и изображены на рис. 1.5, рис. 1.6.
Im
 K
K
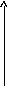 w=∞
w=0
Re
w=∞
w=0
Re

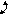



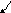 A
A
![]() w
w
Рис. 1.5
A 
![]()
 w w
w w





 o
0
o
0
![]()
![]()
![]()
аб
Рис. 1.6
Асимптотическая ЛАХ приведена на рис. 1.7.
Переходная функция звена имеет вид (рис. 1.8).
 L(w)
h(t)
L(w)
h(t)





 -20 дб/дек
-20 дб/дек

 20lgK
K
20lgK
K
 -40
дб/дек
-40
дб/дек

0 w1 w2 wср lgw 0 t
Рис. 1.7 Рис. 1.8
2.1.3. Колебательное звено второго порядка.
Передаточная функция имеет вид
![]() . (1.18)
. (1.18)
Напомним, что
при
![]() звено становится апериодическим второго
порядка (см. выражение (1.13)).
звено становится апериодическим второго
порядка (см. выражение (1.13)).
Величина
![]() в (1.18) представляет частоту собственных
колебаний.
в (1.18) представляет частоту собственных
колебаний.
АФХ, АЧХ и ФЧХ колебательного звена описываются выражениями:
![]() (1.19)
(1.19)
![]() (1.20)
(1.20)
![]() (1.21)
(1.21)
и изображены на рис. 1.9, рис. 1.10 и рис. 1.11.
 Im
Im
K



 w=∞
w=0
Re
w=∞
w=0
Re

![]()
 A
w
A
w
![]()
Рис. 1.9



 A
A ![]()
![]()
![]() w
w


 w0
w0 




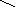
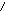

![]()
![]()
![]()
![]()
![]()


 K
K



![]()
![]()
w
0 w0
Рис. 1.10 Рис. 1.11
ЛАХ звена равна
![]() (1.22)
(1.22)
Асимптотическая ЛАХ приведена на рис. 1.12. Переходная функция – на
рис. 1.13.
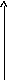

 L(w)
h(t
L(w)
h(t


 20lgK
20lgK


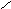


 -40
дб/дек
K
-40
дб/дек
K
lg
![]() w
t
w
t



 0
0
![]() 0
0
![]()
Рис. 1.12 Рис. 1.13
2.2. Интегрирующие звенья
2.2.1. Идеальное интегрирующее звено.
Данное звено имеет передаточную функцию
![]() (1.23)
(1.23)
АФХ, АЧХ и ФЧХ имеют вид:
![]() (1.24)
(1.24)
![]() (1.25)
(1.25)
![]() (1.26)
(1.26)
и изображены на рис. 1.14.

 Im A
Im A
![]()
Re w w



 0
w=∞ 0
0
0
w=∞ 0
0

w
![]()
w=0
а б в
Рис. 1.14
ЛАХ данного звена равна
![]() (1.27)
(1.27)
и изображена на рис. 1.15.
Переходная функция (см. ранее приведённый рис. 1.1, а) идеального интегрирующего звена
![]() (1.28)
(1.28)



 L(w)
L(w)
 20lg
K -20
дб/дек
20lg
K -20
дб/дек
lg w
0 wср=K
Рис. 1.15
2.2.2. Изодромное звено (пропорционально-интегрирующее звено).
Это звено имеет передаточную функцию
![]() (1.29)
(1.29)
т.е. его можно представить как параллельное соединение интегрирующего и пропорционального (безынерционного) звенья. После простых преобразований это звено можно также записать в виде:
![]() (1.30)
(1.30)
где (1+τs) -форсирующее звено,τ =K2/K1.
Таким образом, в соответствии с (1.30) изодромное звено может быть также представлено как последовательное соединение интегрирующего и форсирующего звеньев.
2.3. Дифференцирующие звенья
2.3.1. Идеальное дифференцирующее звено.
Передаточная функция данного звена
![]() (1.31)
(1.31)
АФХ, АЧХ и ФЧХ имеют вид:
![]() (1.32)
(1.32)
![]() (1.33)
(1.33)
![]() (1.34)
(1.34)
и изображены на рис. 1.16.
I





 m w=∞ A
m w=∞ A
![]()
![]()
w
![]()
 0 0 0
0 0 0
w=0 Re w w
а б в
Рис. 1.16
ЛАХ звена равна
![]() (1.35)
(1.35)
и изображена на рис. 1.17.
L(w)



 +20
дб/дек
+20
дб/дек
20 lgK lgw
1/K 1
Рис. 1.17
Переходная функция звена
![]() (1.36)
(1.36)
2.3.2. Реальное дифференцирующее звено.
Передаточная функция звена
![]() . (1.37)
. (1.37)
АФХ, АЧХ и ФЧХ равны соответственно:
![]() (1.38)
(1.38)
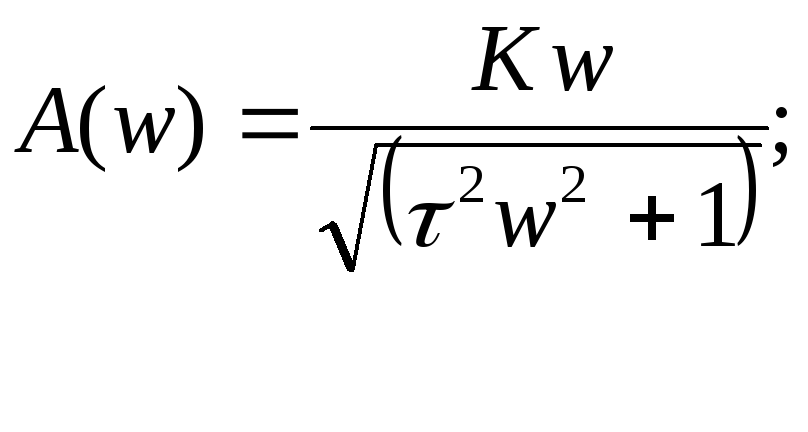 (1.39)
(1.39)
![]() (1.40)
(1.40)
и изображены на рис. 1.18.
 Im A φ
Im A φ


 w=1/τ K/τ
w=1/τ K/τ
![]()




 w
w

 A φ
π/4
A φ
π/4



 w=0 w=∞
w=0 w=∞

0
Re 0
w 0
1/τ w
K/τ
