13.2. Формула Ньютона — Лейбница

Теорема. Если функция непрерывна на сегменте и – первообразная функции на этом отрезке, то

.

(13.2)

Формула (13.2) называется формулой Ньютона — Лейбница. Эта формула дает правило вычисления определенного интегра­ла.

Пример 13.1.

.

Пример 13.2.

.

Пример 13.3.

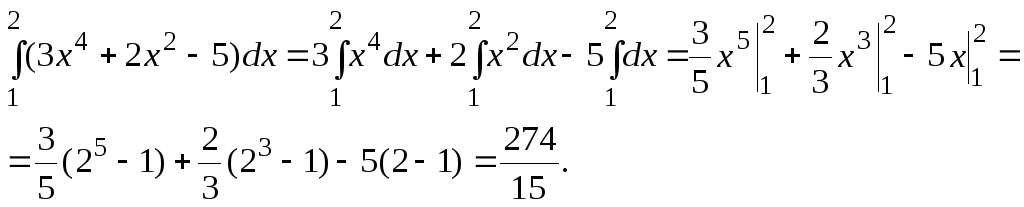
13.3. Свойства определенного интеграла

Рассмотрим непрерывную на отрезке функцию .

1. Определенный интеграл от функции с равными верх­ним и нижним пределами интегрирования равен нулю

.

(13.3)

2. Постоянный множитель можно выносить за знак определенного интеграла

.

(13.4)

3. Определенный интеграл от суммы двух функций равен сум­ме определенных интегралов от этих функций

.

(13.5)

Это свойство распространяется на случай алгебраической суммы любого конечного числа функций.

4. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный

.

(13.6)

5. Интеграл по отрезку равен сумме интегралов по его частям

,

(13.7)

где .

13.4. Замена переменной под знаком определенного интеграла

Предположим, что функция непрерывна на отрезке , функция имеет на отрезке непрерывную производную, при этом и , . Тогда формула замены переменной в определенном интеграле выглядит следующим образом:

.

(13.8)

Пример 13.4. Вычислим интеграл . Воспользуемся подстановкой . Согласно (13.8), получаем

.

13.5. Интегрирование по частям в определенном интеграле

Формула

(13.9)

называется формулой интегрирования по частям для определенного интеграла.

Пример 13.5. Вычислим интеграл . Обозначим , , получим

.

13.6. Приложения определенного интеграла

Определенный интеграл является некоторым числом. Смысл этого числа зависит от геометрического, физического, биологического и пр. смысла функции .

Если переменная является временем, а– скоростью движения некоторого тела, то определенный интеграл равен длине пути, пройденного за время .

Если – производительность труда, то определенный интеграл равен объему продукции, выпущенной за промежуток времени .

Если – перемещение, а – сила, действующая на перемещаемое тело, то определенный интеграл численно равен работе силы на пройденном пути.

Если рассматривается как график некоторой функции, то определенный интеграл численно равен площади соответствующей криволинейной трапеции и т.д.

Пример 13.6. Найти путь, пройденный материальной точкой за четвертую секунду, если скорость ее прямолинейного движения м/с.

Пример 13.7. Производительность труда рабочего задается функцией ден.ед./час; где время в часах от начала работы. Найти объем продукции (в стоимостном выражении), произведенный за рабочий день, если его продолжительность 8 часов.

Пример 13.8.

Найти площадь фигуры, ограниченной графиком функции , осью и прямой (рис. 13.2).

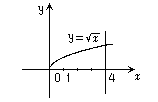
Рис.13.2

Решение задач на вычисление площадей плоских фигур упрощает следующая теорема.

Теорема. Пусть на отрезке заданы непрерывные функции и такие, что . Тогда площадь фигуры, заключенной между кривыми и на отрезке вычисляется по формуле

.

(13.10)

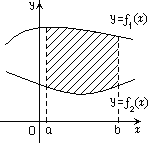
Рис.13.3

Пример 13.9. Найти площадь фигуры, ограниченной графиком функции и (рис. 13.4).

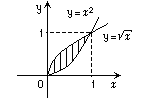
Рис. 13.4

Найдем точки пересечения графиков функций и . Их координаты (0;0) и (1;1). Следовательно,

Если граница криволинейной трапеции составлена из нескольких линий, удобно пользоваться формулой (13.7).

Пример 13.10. Найти площадь фигуры, ограниченной графиками функций , и осью , находящейся в первой четверти координатной плоскости (рис. 13.5).

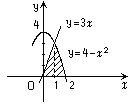
Рис. 13.5

Графики функций и пересекаются в т., линия пересекает ось в точке , линия пересекает ось в точке . Площадь криволинейной трапеции равна

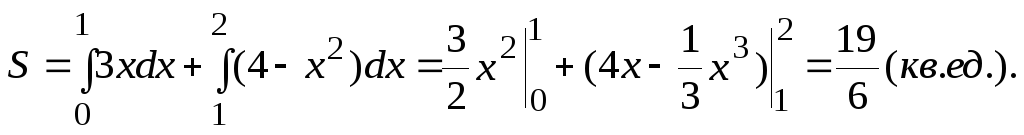
УПРАЖНЕНИЯ

Вычислить определенный интеграл

13.11. 13.12. 13.13. 13.14.

13.15. 13.16. 13.17.

13.18. 13.19. 13.20.

13.21. 13.22. 13.23. 13.24. 13.25. 13.26.

13.27. 13.28. 13.29.

13.30. 13.31. 13.32.

13.33. 13.34. 13.35.

13.36. 13.37. 13.38.

13.39. 13.40. 13.41.

13.42. 13.43. 13.44.

13.45. 13.46. 13.47.

13.48. 13.49. 13.50.

13.51.

13.52. Найти путь, пройденный материальной точкой от начала движения до ее остановки, если скорость ее прямолинейного движения м/с.

13.53. Стоимость перевозки одной тонны груза на 1 км задается функцией (ден.ед./км). Определить затраты на перевозку одной тонны груза на расстояние 20 км.

13.54. Найти площадь фигуры, ограниченной графиком функции и осью .

13.55. Найти площадь фигуры, ограниченной графиками функций , , и осью , находящейся в первой четверти координатной плоскости.

13.56. Найти площадь фигуры, ограниченной графиками функций и .

13.57. Найти площадь фигуры, ограниченной графиками функций, и осью .

13.58. Найти площадь фигуры, ограниченной графиками функций и .

13.59. Найти площадь фигуры, ограниченной графиками функций и .

13.60. Найти площадь фигуры, ограниченной графиками функций , и , находящейся в первой четверти координатной плоскости.

13.61. Найти площадь фигуры, ограниченной графиками функций , и осью .

13.62. Найти площадь фигуры, ограниченной графиками функций , , осью и осью .

13.63. Найти площадь фигуры, ограниченной графиками функций и .

13.64. Найти площадь фигуры, ограниченной графиками функций , , и осью .

13.65. Найти площадь фигуры, ограниченной графиком функции и осью .

13.66. Найти площадь фигуры, ограниченной графиком функции и осью .

13.67. Найти площадь фигуры, ограниченной графиками функций, и осью .

13.68. Найти площадь фигуры, ограниченной графиком функции и осью .

13.69. Найти площадь фигуры, ограниченной графиками функций и .

13.70. Найти площадь фигуры, ограниченной графиками функций , и осью .

13.71. Найти площадь фигуры, ограниченной графиками функций и .

13.72. Найти площадь фигуры, ограниченной графиками функций и .

О Т В Е Т Ы К У П Р А Ж Н Е Н И Я М