-51-

Раздел 6 основы интегрального исчисления

Глава 12. Неопределенный интеграл

12.1. Понятие первообразной функции. Неопределенный интеграл

Рассмотрим задачу нахождения функции по ее производной.

Функция называется первообраз­ной для функции на не-

котором интервале, если на этом интервале выполняется .

Пример 12.1. Функция является первообразной функ­ции на всей числовой оси, так как для любого х выполняется равенство . Вместе с функцией первообразной для является и любая функция , где С – произвольная постоянная.

Теорема. Если является первообразной для функции , то всякая функция , где С – произвольное постоянное число, также является первообразной для .

Доказательство. Найдем производную

.

Отсюда следует, что – первообразная.

Теорема. Две первообразные одной и той же функции отличаются на постоянную величину.

Доказательство. Пусть и – две первообразные для функции . Рассмотрим разность .

Найдем . По следствию из теоремы Лагранжа (п. 10.1) , следовательно,

.

Из данных теорем следует, что зная одну первообразную для функции , можно получить все ее первообразные, прибавляя к всевозможные постоянные.

Множество функций , где С – произвольная постоянная, представляет собой семейство первообразных данной функции, графики которых являются параллельными линиями (рис.12.1).

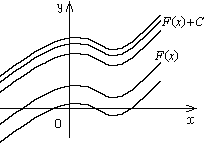
Рис. 12.1

Семейство первообразных назы­вается неопределенным интегралом от функции и обозначается символом .

Функция называется подынтегральной функ­цией, – подынтегральным выражением, – переменной интегрирования, знак – знаком интеграла.

Таким образом,

,

(12.1)

где , С – сonst.

Операция нахождения первообразной для данной функции называется неопределенным интегрированием. Дифференцирование и интегрирование – это две взаимно обратные операции.

Достаточным условием интегрируемости функции на некотором интервале является непрерывность этой функции на данном интервале.

12.2. Свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна подынтегральной функции

.

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению

.

3. Постоянный множитель можно вынести за знак интеграла

.

(12.2)

4. Интеграл от суммы двух функций равен сумме интегралов от этих функций

.

(12.3)

12.3. Таблица интегралов

. . . . . . .

. . . . .

12.4. Методы интегрирования

1. Метод разложения

Метод разложения связан с приведением подынтеграль­ного выражения к табличной форме путем алгебраических преобразований и при­менения свойств неопределенных интегралов.

Пример 12.2.

.

Пример 12.3.

Пример 12.4.

Пример 12.5.

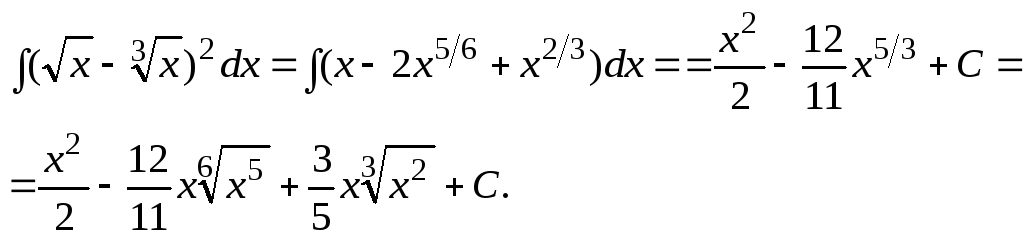
Пример 12.6.

.

Пример 12.7.

.

2. Замена переменной интегрирования

Сделаем подстановку , где – функция, имеющая непрерывную производную. Тогда , и

,

(12.4)

Формула (12.4) называется формулой замены переменной в неопределенном интеграле.

Вместо подстановки иногда удобно применять подстановку .

При замене переменной удобно пользоваться следующими правилами:

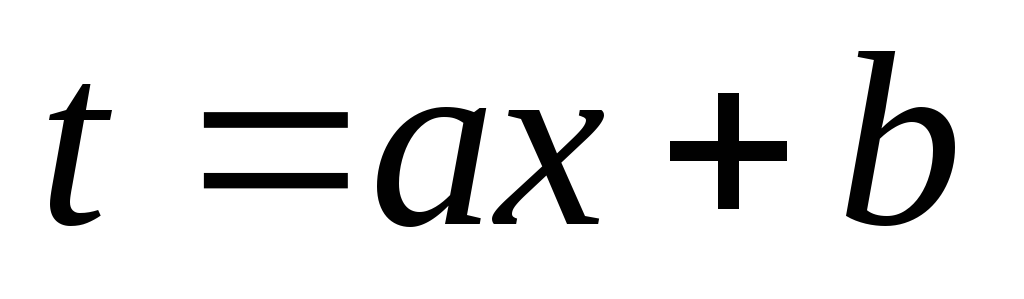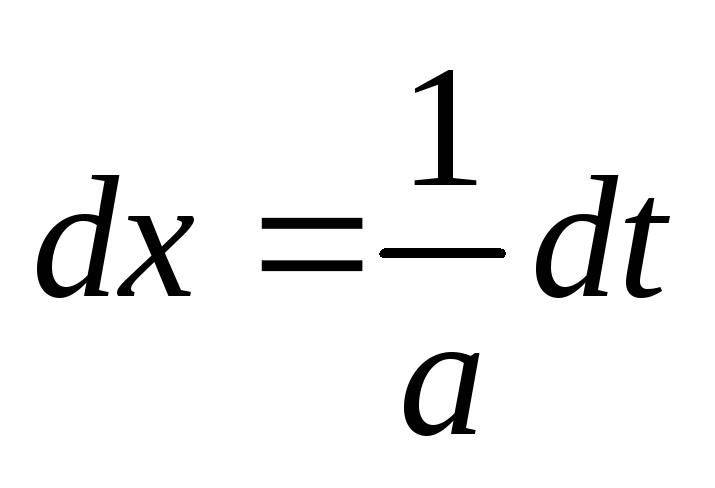1. Если интеграл является табличным, то интеграл может быть найден с помощью подстановки , т.к. , следовательно, и

.

(12.5)

Пример 12.8. Вычислим интеграл . Делаем подстановку и находим . Отсюда

.

Пример 12.9. Вычислим интеграл . Делаем подстановку: и находим , откуда . Данный интеграл запишется в виде

.

Пример 12.10. Вычислим интеграл . Делаем подстановку: и находим , откуда . Данный интеграл запишется в виде

.

Пример 12.11. Вычислим интеграл . При интегрировании дробей вида в квадратном трехчлене выделяется полный квадрат некоторого линейного выражения, а затем осуществляется замена этого выражения на новую переменную .

.

Здесь , .

2. Если подынтегральная функция является произведением двух множителей, один из которых зависит от некоторой функции 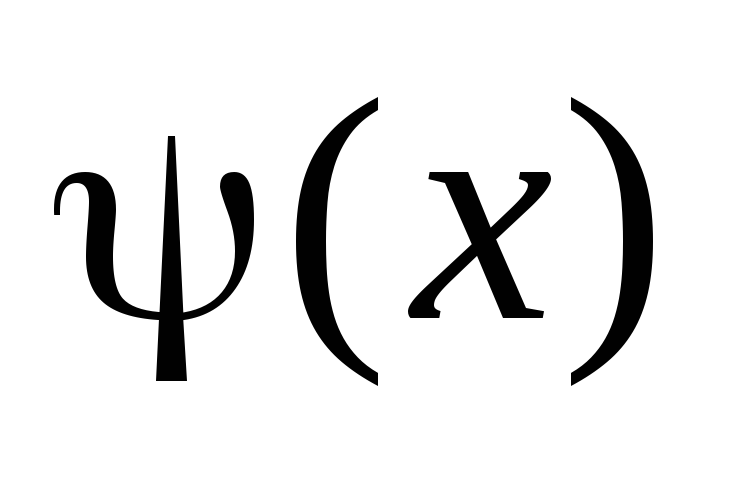, а другой является производной этой функции (с точностью до постоянного множителя), то нужно применять подстановку .

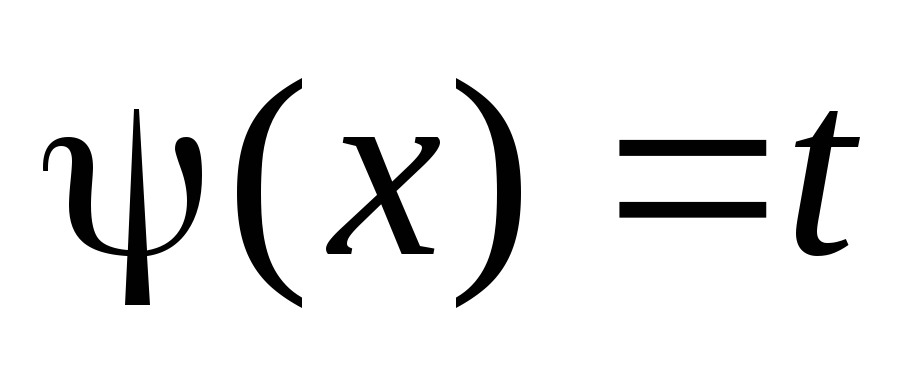Пример 12.12. Вычислим интеграл . Делаем подстановку и находим . Данный интеграл запишется в виде

.

Пример 12.13. Вычислим интеграл . Заменяем и находим . Интеграл примет вид

.

Пример 12.14. Вычислим интеграл . Делаем замену и находим . Интеграл примет вид

.